Вычисление обратной матрицы с помощью алгебраических дополнений

Задана квадратная матрица 3–го порядка

A =	    	a11 a12 a13 a21 a22 a23 a31 a32 a33	    

Для вычисления обратной матрицы методом алгебраических дополнений

1. Вычисляем определитель матрицы A . Если det A ≠ 0 , то матрица A имеет обратную.

2. Составляем матрицу из алгебраических дополнений элементов матрицы A

˜A =	    	A11 A12 A13 A21 A22 A23 A31 A32 A33	    	.

3. Находим транспонированную матрицу:

˜AT =	    	A11 A21 A31 A12 A22 A32 A13 A23 A33	    	.

4. Разделив матрицу ˜AT на определитель, получаем искомую обратную матрицу:

A−1 =   1 det A    ·	    	A11 A21 A31 A12 A22 A32 A13 A23 A33	    	.

5. Проверяем, что A · A⁻¹ = E , и записываем ответ.

Транспонированная матрица — матрица  , полученная из исходной матрицы   заменой строк на столбцы.

Формально, транспонированная матрица для матрицы   размеров   — матрица   размеров  , определённая как A^T[i, j] = A[j, i].

Например,

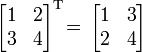      и      

[править]Свойства транспонированных матриц

• 

Дважды транспонированная матрица А равна исходной матрице А.

• 

Транспонированная сумма матриц равна сумме транспонированных матриц.

• 

Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.

• 

При транспонировании можно выносить скаляр.

• 

Определитель транспонированной матрицы равен определителю исходной матрицы.