Понятие размерности векторного пространства и базиса.

Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статье линейная зависимость системы векторов, свойства линейной зависимости и независимости.

Определение.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Определение.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n-мерных векторов.

Покажем, что размерность этого пространства равна n.

Возьмем систему из n единичных векторов вида 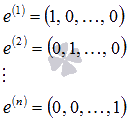  Примем эти векторы в качестве строк матрицы А. В этом случае матрица А будет единичной матрицей размерности n на n. Ранг этой матрицы равен n (при необходимости смотрите статью ранг матрицы: определение, методы нахождения). Следовательно, система векторов   линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе   равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы   являются базисом этого пространства.

Из последнего утверждения и определения базиса можно сделать вывод, что любая системаn-мерных векторов, число векторов в которой меньше n, не является базисом.

Теперь переставим местами первый и второй вектор системы  . Легко показать, что полученная система векторов   также является базисом n-мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n. Таким образом, система из n векторов   линейно независима и является базисом n-мерного векторного пространства.

Если переставить местами другие векторы системы  , то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n-мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Билет 6

n-мерные векторы, операции над ними.

В разделе векторы - основные определения мы ввели понятие вектора в двумерном пространстве (на плоскости) и в трехмерном пространстве. В этой статье мы отойдем от геометрического истолкования вектора и посмотрим на него не как на направленный отрезок, а как на упорядоченный набор чисел с присущими ему свойствами. То есть, мы рассматрим векторы с позиций алгебры, что позволит расширить понятие вектора на случай n-мерного пространства. Итак, мы дадим понятие n-мерного вектора, зададим операции над n-мерными векторами, перечислим свойства этих операций и покажем их применение при решении задач.

Определение.

Упорядоченная совокупность n действительных или комплексных чисел  называется n-мерным вектором. Числа   называются координатами вектора.

Векторы обозначаются строчными латинскими буквами, например, a, b, c и т.п., координаты вектора указываются в скобках.

Если записать вектор a как  , то имеем вектор-строку; если записать  , то имеем вектор-столбец. Это две формы записи одного и того же объекта - n-мерного вектора.

Обратите внимание: при обозначении n-мерных векторов стрелочка сверху над буквой (которая ставится при обозначении вектора на плоскости и в трехмерном пространстве) отсутствует.

Определение.

Вектор  , все координаты которого равны нулю, называют нулевым вектором.

Определение.

Вектор   называется противоположным вектору  .

Для n-мерных векторов задаются две операции: сложение векторов и умножение вектора на число.

Определение.

Суммой двух векторов   и   называется вектор, координаты которого равны сумме соответствующих координат, то есть,  .

Следует отметить, что складывать можно только векторы количество координат которых совпадает. Операция сложения для векторов, имеющих различное число координат, не определена.

Определение.

Произведением действительного или комплексного числа   и вектора   называется вектор, координаты которого равны соответствующим координатам вектора а, умноженным на  , то есть,  .

Введенные таким образом операции над n-мерными векторами при n = 2 и n = 3 полностью согласуются с операциями сложения и умножения вектора на число на плоскости и в трехмерном пространстве в геометрическом смысле. Под координатами двумерного или трехмерного вектора в этом случае понимаем координаты вектора в заданной прямоугольной системе координат на плоскости или в пространстве соответственно.

Перечислим свойства операций над n-мерными векторами.

Для любых векторов   и произвольных действительных или комплексных чисел   справедливо:

1. свойство коммутативности сложения векторов a + b = b + a;

2. свойство ассоциативности векторов (a + b) + c = a + (b + c);

3. существует нейтральный вектор по операции сложения, им является нулевой вектор, a + 0 = a;

4. для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a + (-a) = 0;

5. Сочетательное свойство умножения  .

6. Первое распределительное свойство  .

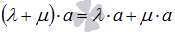7. Второе распределительное свойство  .

8. существует нейтральное число по операции умножения, им является единица .

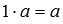Эти свойства справедливы в силу свойств операций сложения и умножения действительных или комплексных чисел.

Операции вычитания векторов как таковой нет, так как разность векторов a и b есть сумма векторов a и -b.

Перечисленные свойства операций позволяют выполнять преобразования в выражениях содержащих векторы по тем же принципам, что и в числовых выражениях.

Билет 7