
- •4.4 Решение систем линейных уравнений методом Гаусса
- •Определители малых порядков
- •Метод Крамера.
- •Понятие размерности векторного пространства и базиса.
- •Операции над матрицами, свойства операций.
- •Вычисление обратной матрицы с помощью алгебраических дополнений
- •Ранг матрицы
- •Определение
- •Определение ранга матрицы
- •Вычисление ранга матрицы с помощью миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Системы линейных однородных уравнений. Фундаментальная система решений
- •Деление с остатком
- •Теорема Безу
- •Доказательство
- •Следствия
Теорема Безу
Теорема Безу утверждает,
что остаток от деления многочлена
на двучлен ![]() равен
равен ![]() .
.
Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).
Доказательство
Поделим
с остатком многочлен
на
многочлен ![]() :
:
![]()
Так
как ![]() ,
то
,
то ![]() —
многочлен степени не выше 0. Подставляя
—
многочлен степени не выше 0. Подставляя ![]() ,
поскольку
,
поскольку ![]() ,
имеем
,
имеем ![]() .
.
Следствия
Число a является корнем многочлена тогда и только тогда, когда делится без остатка на двучлен (отсюда, в частности, следует, что множество корней многочлена тождественно множеству корней соответствующего уравнения
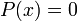 ).
).Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.
Кратные корни
Определение. Число
 называется
корнем полинома
,
если
называется
корнем полинома
,
если  .
.В силу теоремы Безу это равносильно тому, что
 .
.Определение. Число называется корнем кратности
 полинома
,
если
полинома
,
если  и
и  .
Корни кратности 1 называются простыми
корнями, корни кратности больше 1
называются кратными корнями.
.
Корни кратности 1 называются простыми
корнями, корни кратности больше 1
называются кратными корнями.Теорема. Если — корень кратности полинома , то — корень кратности
 полинома
полинома  .
Если
—
общий корень
.
Если
—
общий корень  ,
то
—
кратный корень
.
,
то
—
кратный корень
.Доказательство. Пусть — корень кратности полинома .


1. Если
 ,
то
—
корень кратности
многочлена
.
,
то
—
корень кратности
многочлена
.2. Если корень , то и, значит, — кратный корень многочлена .
Теорема Виета
Как связаны между собой корни квадратного трехчлена x2 + px + q и его коэффициенты p и q? Ответ на этот вопрос дает теорема, которая носит имя “отца алгебры”, французского математика Ф. Виета, жившего в конце XVI века.
Теорема.
Сумма корней квадратного трехчлена x2 + px + q равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q.
Доказательство. Пусть x1 и x2 – различные корни квадратного трехчлена x2 + px + q. Теорема Виета утверждает, что имеют место следующие соотношения:
x1 + x2 = –p
x1 x2 = q
Для доказательства подставим каждый из корней в выражение для квадратного трехчлена. Получим два верных числовых равенства:
x12 + px1 + q = 0
x22 + px2 + q = 0
Вычтем эти равенства друг из друга. Получим
x12 – x22 + p (x1 – x2) = 0
Разложим разность квадратов и одновременно перенесем второе слагаемое в правую часть:
(x1 – x2) (x1 + x2) = –p (x1 – x2)
Так как по условию корни x1 и x2 различны, то x1 – x2 0 и мы можем сократить равенство на x1 – x2. Получим первое равенство теоремы:
x1 + x2 = –p
Для доказательства второго подставим в одно из написанных выше равенств (например, в первое) вместо коэффициента p,равное ему число – (x1 + x2):
x12 – (x1 + x2) x1 + q = 0
Преобразуя левую часть, получаем:
x12 – x12 – x2 x1 + q = 0
x1 x2 = q, что и требовалось доказать.
Комментарий. Теорема Виета замечательна тем, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные выражения x1 + x2 и x1 x2. Так, еще не зная, как вычислить корни уравнения x2 – x – 1 = 0, мы, тем не менее, можем сказать, что их сумма должна быть равна 1, а произведение должно равняться –1.
Теорема Виета позволяет угадывать целые корни квадратного трехчлена. Так, находя корни квадратного уравнения x2 – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: 6 = 2 3, 2 + 3 = 5. Отсюда должно следовать, что числа 2 и 3 являются искомыми корнями. Эту догадку можно аккуратно доказать.
Теорема. Если числа x1 и x2 удовлетворяют соотношениям x1 + x2 = –p и x1 x2 = q, то они удовлетворяют квадратному уравнению x2 + px + q = 0.
Доказательство. Из первого из данных равенств выразим x2 и подставим во второе: x2 = –p – x1, x1 x2 = x1 (–p – x1) = q. Получаем –x12 – px1 = q или x12 + px1 + q = 0. Это означает, что число x1 является корнем квадратного уравнения x2 + px + q = 0. Если бы наоборот мы выразили x1 через x2, то получили бы и для x2 аналогичное соотношение:x22 + px2 + q = 0. Теорема доказана.
Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни.
Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.
Формулировка
Если ![]() —
корни многочлена
—
корни многочлена
![]()
(каждый
корень взят соответствующее его кратности
число раз), то коэффициенты ![]() выражаются
в виде симметрических
многочленов от
корней, а именно:
выражаются
в виде симметрических
многочленов от
корней, а именно:
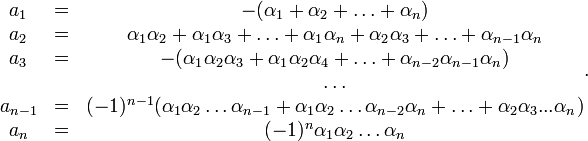
Иначе
говоря ![]() равно
сумме всех возможных произведений
из
корней.
равно
сумме всех возможных произведений
из
корней.
Если
старший коэффициент многочлена ![]() ,
то для применения формулы Виета необходимо
предварительно разделить все коэффициенты
на
,
то для применения формулы Виета необходимо
предварительно разделить все коэффициенты
на ![]() (это
не влияет на значение корней многочлена).
В этом случае формулы Виета дают выражение
для отношений всех коэффициентов к
старшему. Из последней формулы Виета
следует, что если корни многочлена
целочисленные, то они являются делителями
его свободного члена, который также
целочисленен.
(это
не влияет на значение корней многочлена).
В этом случае формулы Виета дают выражение
для отношений всех коэффициентов к
старшему. Из последней формулы Виета
следует, что если корни многочлена
целочисленные, то они являются делителями
его свободного члена, который также
целочисленен.
[править]Доказательство
Доказательство
осуществляется рассмотрением равенства,
полученного разложением многочлена по
корням, учитывая, что ![]()
![]()
Приравнивая коэффициенты при одинаковых степенях (теорема единственности), получаем формулы Виета.
Билет 16
Алгоритм Евклида для целых чисел
Пусть ![]() и
—
целые числа, не равные одновременно
нулю, и последовательность чисел
и
—
целые числа, не равные одновременно
нулю, и последовательность чисел
![]()
определена
тем, что каждое ![]() —
это остаток от деления предпредыдущего
числа на предыдущее, а предпоследнее
делится на последнее нацело, то есть
—
это остаток от деления предпредыдущего
числа на предыдущее, а предпоследнее
делится на последнее нацело, то есть
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда
НОД(a,b),
наибольший общий делитель
и
,
равен ![]() ,
последнему ненулевому члену этой
последовательности.
,
последнему ненулевому члену этой
последовательности.
Существование таких ![]() ,
то есть возможность деления с
остатком
на
для
любого целого
и
целого
,
то есть возможность деления с
остатком
на
для
любого целого
и
целого ![]() ,
доказывается индукцией по m.
,
доказывается индукцией по m.
Корректность этого алгоритма вытекает из следующих двух утверждений:
Пусть ![]() ,
тогда НОД (a, b) = НОД (b, r).
,
тогда НОД (a, b) = НОД (b, r).
Доказательство [показать]
НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).
Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
