
3. Алгоритм форда - фалкерсона
Рассмотрим алгоритм Форда-Фалкерсона для фиксированной конфигурации сети.
Идея алгоритма
Алгоритм начинает работу с начального допустимого потока (возможно, нулевого). Затем осуществляются попытки увеличить величину потока с помощью систематического поиска всех возможных цепей из s в t, на которых можно увеличить величину потока (дополняющие цепи).
Поиск дополняющих цепей производится путем расстановки меток, которые указывают, на каких дугах и на сколько можно увеличить поток. Когда найдена одна из таких цепей, поток вдоль нее увеличивается. После чего все метки стираются, и вновь полученный поток используется в качестве исходного при новой расстановке меток.
Алгоритм заканчивает работу, когда нельзя найти ни одну дополняющую цепь. Последний найденный поток является максимальным.
Важной частью алгоритма является этап расстановки меток. Каждая вершина может находиться в одном из трех состояний:
вершина помечена и просмотрена (т.е. вершина имеет метку и все смежные с ней вершины «обработаны»);
вершина помечена, но не просмотрена (т.е. вершина имеет метку, но смежные с ней вершины не «обработаны»);
вершина.
не помечена;
Метка некоторой
вершины
![]() имеет вид
имеет вид
![]() .
Часть меткиозначает, что поток может
быть увеличен вдоль дуги . Часть метки
.
Часть меткиозначает, что поток может
быть увеличен вдоль дуги . Часть метки
![]() означает, что поток может быть уменьшен
вдоль дуги . В обоих случаях
означает, что поток может быть уменьшен
вдоль дуги . В обоих случаях
![]() показывает максимальную величину, на
которую можно увеличить поток от
показывает максимальную величину, на
которую можно увеличить поток от
![]() к
вдоль дополняющей цепи.
к
вдоль дополняющей цепи.
Сначала все вершины не имеют меток.
Описание алгоритма
Входными данными алгоритма являются:
матрица пропускных способностей дуг
начальный поток, задаваемый матрицей потоков дуг
При завершении работы алгоритм выдает найденный максимальный поток, который определяется матрицей потоков дуг.
Шаг 0. Инициализация.
Положим все дуговые потоки равными нулю: .
Шаг 1. Назначить вершине метку .
Теперь вершина помечена, но не просмотрена. Все остальные вершины не помечены.
Шаг 2. Просмотр помеченных вершин.
Выбрать некоторую помеченную, но не просмотренную вершину ; пусть ее метка будет .
Каждой непомеченной вершине
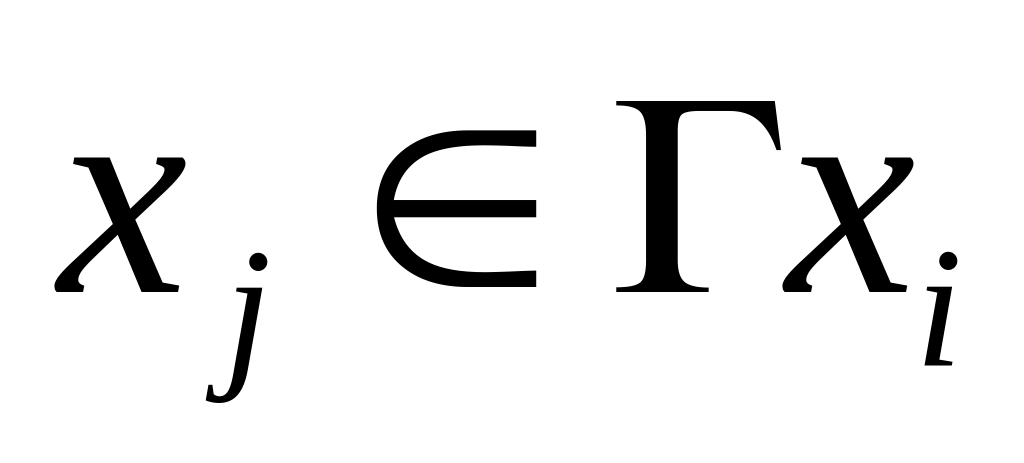 ,
для которой , назначить метку , где
,
для которой , назначить метку , где
![]() .
.
Каждой непомеченной вершине , для которой назначить метку
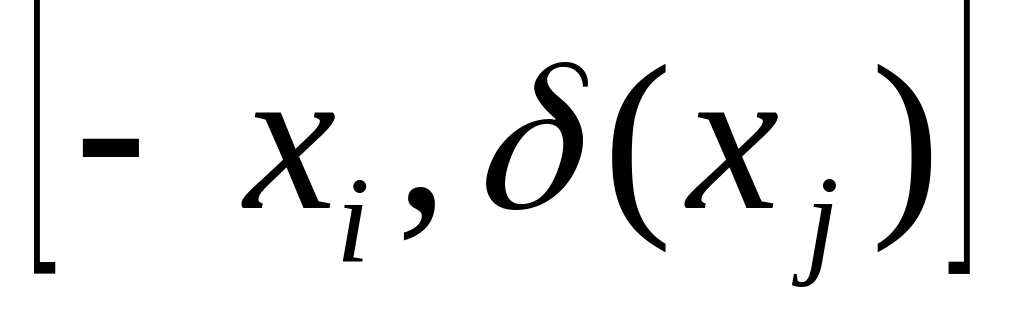 ,
где
,
где
![]() .
.
Теперь вершина помечена и просмотрена, а вершина , метка которой назначена в пунктах 1 или 2, помечена, но не просмотрена. Каким-либо образом отмечается, что вершина просмотрена.
Шаг 3. Проверка.
Если на Шаге 2 какая-либо вершина помечена, то:
если помечена вершина , то на Шаг 4;
если помечена любая другая вершина, то на Шаг 2.
Если на Шаге 2 нельзя назначить никаких меток, то алгоритм заканчивает работу с некоторым максимальным потоком.
Шаг 4. Выбрать вершину ; на Шаг 5.
Шаг 5. Увеличение потока.
Если метка вершины имеет вид , то изменить поток вдоль дуги с на .
Если метка вершины имеет вид , то изменить поток вдоль дуги с на
 .
.
Шаг 6. Если , то стереть все метки и вернуться к Шагу 1. При этом используется уже увеличенный поток, найденный на Шаге 5.
Если , то положить ; на Шаг 5.
Пример. Найти максимальный поток и минимальное сечение для графа, пропускная способность каждого ребра равна 1.
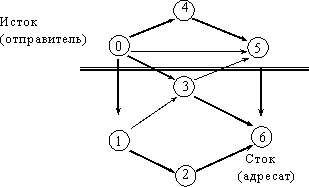
3 – минимальное сечение
3 – максимальный поток
Решение.
1![]() .Пусть
исходный поток будет нулевой: .
.Пусть
исходный поток будет нулевой: .
F |
с(x,y) |
f0(x,y) |
f1(x,y) |
f2(x,y) |
f3(x,y) |
|
||||
0 1 |
1 |
|
0 |
+ |
1 |
|
1 |
|
1 |
|
0 3 |
1 |
|
0 |
|
|
+ |
1 |
|
1 |
|
0 4 |
1 |
|
0 |
|
|
|
|
+ |
1 |
|
0 5 |
1 |
|
0 |
|
|
|
|
|
|
+ |
1 2 |
1 |
|
0 |
|
|
|
|
+ |
1 |
|
1 3 |
1 |
|
0 |
+ |
1 |
|
1 |
- |
|
|
2 6 |
1 |
|
0 |
|
|
|
|
|
+ |
|
3 5 |
1 |
|
0 |
|
|
+ |
1 |
1 |
|
|
3 6 |
1 |
|
0 |
+ |
1 |
|
1 |
1 |
1 |
|
4 5 |
1 |
|
0 |
|
|
|
|
|
1 |
- |
4 6 |
1 |
|
0 |
|
|
+ |
1 |
1 |
1 |
|
2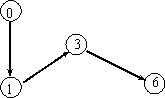 .
Пометим ребра 01, 13, 36 знаком + и направим
по найденному маршруту поток 1.
.
Пометим ребра 01, 13, 36 знаком + и направим
по найденному маршруту поток 1.
Маршрут для потока f1(x, y)
3. Пометим ребра 03, 35, 56 знаком (+) и направим по найденному маршруту поток 1.
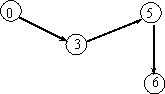
Маршрут для потока f2(x, y)
Полученный поток f2 (x, y) содержит по крайней мере одну насыщенную дугу – то есть является "полным" потоком.
4. Попробуем улучшить полученный поток:
1. Пометим знаком (+) узел 0.
2. Пометим знаком (+) ненасыщенные дуги 04 и 45. Так как из вершин 5 выходит насыщенная дуга 56, пометим знаком (-) ненулевой поток 35. Так как из вершины 3 выходит насыщенная дуга 36, пометим знаком (-) ненулевой дуги 13. Пометим знаком (+) ненасыщенные дуги 12, 26.
3. На вновь открытом маршруте +0.4+4.5-3.5-1.3+1.2+2.6 вычислим приращение "полного" потока равен 1.
4. Пометим ребро 05 символом (+), так как из вершины 5 выходит насыщенная дуга 56, пометим знаком (–) ненулевой поток 45. То есть все узлы сети можно разбить на два непересекающихся множества
Β = {0,4,5} и Β= {1,2,3,6}.
