- •Методы и модели в экономике
- •1. Детерминированные сетевые модели. Области и условия применений. Критический путь в сетевой модели.
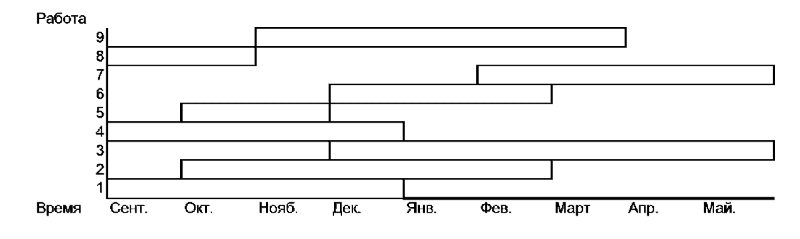
- •Ленточные графики Ганта.
- •7. Методы экспертных оценок в экономике. Необходимость и условия применения. Основные этапы проведения экспертизы.
- •8. Метод дельфи. Алгоритм, цель использования метода.
- •10. Согласованность мнений экспертов при ранжировании объектов. Коэффициент координации.
- •Выводы:
Методы и модели в экономике
1. Детерминированные сетевые модели. Области и условия применений. Критический путь в сетевой модели.
Любая поставленная цель требует детальной проработки. Приступая к составлению плана работ, мы можем «сконструировать» весь процесс в виде графика, где часть работ выполняется последовательно, а другая часть параллельно разными исполнителями.
Единую систему выполнения всей программы можно представить в виде совокупности работ, действий и результатов. Математической моделью всего комплекса работ является сетевая модель.
Детерминированные сетевые модели – это модели с детерминированной топологией и детерминированной метрикой, программный аппарат данного вида моделей является разработанным.
Целью анализа и расчета сетевой модели является получение параметров, необходимых для применения решений по сроку, стоимости, маршруту, обеспеченности выбранного плана и прогнозу действий. Сетевая модель позволяет производить эксперименты и выяснять, к каким результатам приведет то или иное измерение в условиях собственной задачи: концентрирует внимание руководителя фирмы на самых важных работах комплекса, на перераспределение времени, ресурсов или измерении качественных показателей для достижения надежной гарантии выполнения работ в директивно намеченный срок.
Основой всех систем сетевого планирования и управления является использование сетевых моделей. Объектом моделирования является комплексы работ (н-р: комплекс работ по научной проблеме, комплекс мероприятий по внедрению нового технологического процесса). Объем и характер комплекса могут быть различными. Важными свойствами объекта моделирования являются:
А) возможность представления его в виде совокупности отдельных взаимосвязанных работ.
Б) наличие очередности выполнения между этими работами.
В) наличие цели, для достижения которой предназначаются все работы комплекса.
Работа (операция) – основной элемент комплекса. Она представляет собой либо трудовой процесс, в котором участвуют люди, машины, механизмы, либо процесс ожидания. Во всех случаях работа – это процесс, происходящий во времени.
Наиболее важная характеристика работы связана с понятием ее объема. Реальный смысл объема работы может быть весьма различным (трудоемкость в человеко-днях, машино-сменах; физические размеры в кубометрах, тоннах, километрах и т.д.) в наиболее распространенных моделях роль объема играет продолжительность работы. Фиктивная работа (или логическая связь) не требует ни времени, ни ресурсов. Примером фиктивной работы может служить телефонный звонок, разрешающий действительную работу.
Событие – это элемент комплекса, означающий определенное состояние в процессе выполнения комплекса работ. Каждое событие можно охарактеризовать как:
появление условий, позволяющих начать одну или несколько работ комплекса (эти работы по отношению к событию называются непосредственно следующими или выходящими, а событие по отношению к работам - начальным)
окончание одной или нескольких работ комплекса (эти работы по отношению к событию называются непосредственно предшествующими или входящими, а событие по отношению к работам - конечным)
событие, не имеющее непосредственно предшествующих работ, называют исходным; не имеющее непосредственно следующих работ – завершающим событием комплекса.
Событие в отличие от работы не является процессом и не имеет продолжительности. В сетевой модели событие обычно характеризуется составом входящих и выходящих работ. Одним из основных признаков комплекса является наличие отношений порядка между работами. В большинстве случаев эти отношения состоят в том, что некоторые работы не могут быть начаты, прежде чем закончатся другие работы комплекса.
Значение, показывающее самый длинный по продолжительности путь в сетевой модели называется критическим путем и показывает минимально возможное время выполнения всех работ сетевой модели.
Очевидно, что операции критического пути имеют НУЛЕВЫЕ резервы. У некритических операций может быть нулевой свободный резерв и ненулевой полный резерв. Поэтому критерием поиска критического пути является нулевой полный резерв операций.
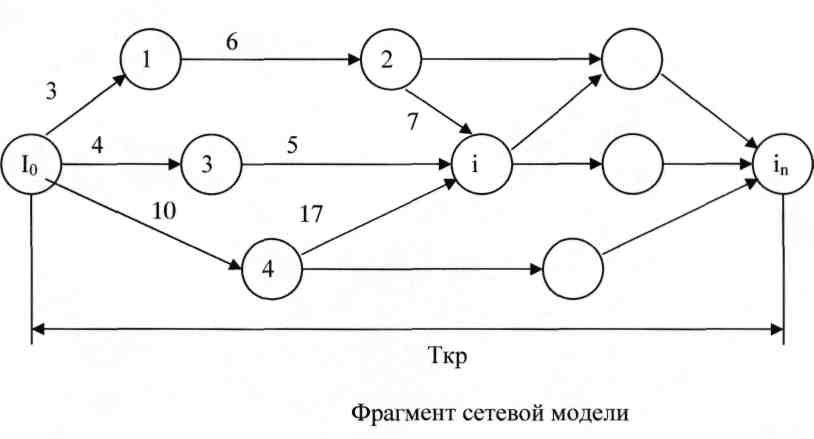
Теорема 1 длина критического пути – это величина λ для самого позднего события Ткр= λiп
Теорема 2 продолжительность max пути, следущ. за i событием = Ткр= λ'i
Теорема 3 если событие принадлежит Ткр, то λi = λ'i
2. Временные параметры событий и работ сетевой модели. полный свободный резервы времени работ.
Временные параметры событий
Сетевая модель позволяет рассчитать наступление времени каждого события календарного, причем топология (i-j) позволяет рассчитать два возможных времени, два момента наступления для каждого события.
Ранний срок наступления событий характеризует самое раннее возможное наступление любого события i относительно времени наступления i. По определению любое событие наступает только тогда, когда выполняется все то, что до него, т.е. до определения max путем, который предш. этому событию.
Tpi = L[Lmax предш. i] = λi (1)
Значение Tpi показывает самый длинный по продолжительности путь в сетевой модели; он называется критическим путем Ткр и показывает минимально возможное время выполнения всех работ сетевой модели.
Позднее время наступления события Tпi - это позднее допустимое время до наступления события.
Tпi = Ткр – t[Lmaxслед. (i)] = χ Ткр –[Ткр– λ'i] = λ'I (2)
Все то, что идет после этого события было выполнено в сроки не превышают Ткр
Чтобы рассчитать позднее время и раннее время необходимо провести расчет по алгоритму Форда в прямой (1) и обратной (2) зависимости.
Резерв времени события характеризует запас времени события (в днях,..), учитывающий возможность перенести срок наступления события, не изменяя при этом срока наступления завершающего события in (т.е. Ткр).
Ri = Tпi – Tpi
Теорема 4 если событие принадлежит критическому пути, то начало время наступления раннего события будет равно времени наступления позднего.
Ткр(iєLкр.)=> Tpi= Tпi
Теорема 5 если событие принадлежит критическому пути, то резерв =0
iєLкр=>Ri=0
Временные параметры работ сетевой модели
Топология сетевой модели позволяет нам рассчитать 2 дополн. времени наступления работы и 2 дополнительных времени окончания работ.
Tрнij - время раннего наступления работы. Каждая работа может быть начата только когда выполнены все работы, входящие в нее
Tрнij = λi= Tpi
Все работы исходящие из какого-либо события будут иметь одинаковое раннее начало, соответственно мы имеем раннее окончание работы.
Tроij= λi+t(ij) =Tрнij+t(ij)
Аналогично можно рассчитать поздние сроки окончания работы, которая зависит от позднего срока наступления события, в которое входит эта работа.
Tij= λ'i= Tпi
Все работы, входящие в событие, будут иметь одинаковое позднее окончание.
Tпнij = Tпоij-t(ij)=λ'i- t(ij)
Таким образом, чтобы рассчитать все временные параметры сетевой модели нам необходимо:
1. построить таблицу порядка
2. сделать расчет по алгоритму формул.
Полный резерв времени работы показывает разницу между поздним и ранним сроками начала (или окончания) работы, т.е.
Rпij= Tпнij - Tрнij = Tпоij - Tроij = λ'i- λi- t(ij)
Показывает насколько можно увеличить продолжительность работы или задержать ранний момент ее начала, не изменяя Ткр
Теорема 6 для того чтобы полный резерв = 0, необходимо и достаточно, чтобы работа принадлежала критическому пути
Теорема 7 если продолжительность работы увеличить на величину ее полного резерва, то Ткр не изменится, изменится Lкр
Теорема 8 если продолжительность работы увеличить на величину L, причем L будет больше, чем полный резерв этой работы, то как следствие мы получим изменение Tкр
Свободный резерв времени работы
На практике работы критического пути являются «узким местом» и требуют дополнительного внимания. Для оперативного управления ходом выполнения работ вычисляется еще один резерв времени работы - свободный резерв времени работы.
Организационно-экономический смысл свободного резерва времени работы: он показывает, на сколько можно увеличить продолжительность работы, или задержать ранний момент ее начала, не изменяя раннего срока начала работ, которые непосредственно следуют за искомой.
Rсij=Tpj-Tpi-t(ij) равен разности значений события и продолжительности работы и значение раннего срока ее окончания λj – λi – t(ij) = Rсij
Выводы о резервах:
временные параметры работ являются элементами планирования, т.к. они связаны с календарными сроками начала и окончания работ
резервы времени являются параметрами управления, т.к. на их основе можно принимать решения об изменении времени выполнения работ.
полный резерв времени работ характеризует запас времени работы относительно всей сетевой модели.
свободный резерв характеризует запасы времени относительно последующих работ
теорема 11 если работы принадлежат критическому пути, ее свободный резерв равен 0
теорема 12 продолжительность max пути, проходящие через работу равна Tкр минус полный резерв
3. Время и стоимость работы. зависимость между ними. Задача «время-стоимость». Организационно-экономическая постановка.
В решении задач маркетинга, менеджмента необходимо учитывать, контролировать и прогнозировать множество факторов - продолжительность работы; стоимость изготовления; количество исполнителей и т.д. Все факторы зависят друг от друга. Иногда эту зависимость определить трудно, но она все равно есть.
Зависимость между длительностью работы и ее стоимостью с некоторой долей условности можно представить в виде аппроксимирующей прямой, имеющей линейную зависимость (рис. 1.16)
C(ij)
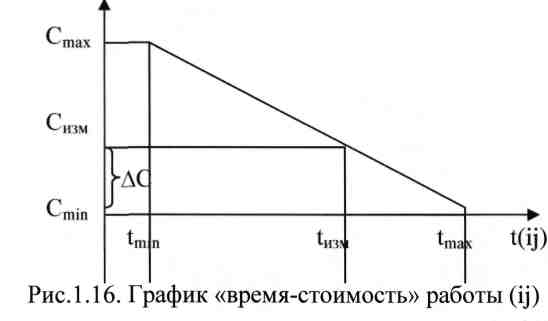
фактически это ломаная
стоимость увеличивается или уменьшается по-разному
в каждой точке рост стоимости будет различным
аппроксимирующая прямая, т.е. чем больше мы стремимся уменьшить время работы, тем дороже будет эта работа стоить
для каждой работы (ij) можно определить скорость изменения стоимости (в каждой точке):
S(ij) = Cmax (ij) – Cmin(ij) / tmax(ij) – tmin(ij), отсюда:
Если время меняется на ∆t, то ∆C=S(ij)*∆t
Если дано Сmin(ij), tmax(ij), S(ij), tmin(ij), то
Cmax(ij)=S(ij) (tmax(ij) – tmin(ij))
S(ij) обычно определяют и задают по нескольким видам работ
4. Алгоритмы решения задачи минимизации общего времени выполнения работ (по сетевой модели) при условии минимизации дополнительных затрат.
Рассмотрим алгоритм оптимизации сетевой модели по критерию «стоимость».
Дано: Сетевая модель. По каждой работе (ij) дается возможный диапазон длительности работы tmin(ij), tmax(ij), минимальная стоимость работы Сmin(ij), коэффициент S(ij). Необходимо найти зависимость Ткр между и суммарными затратами, ставя задачу обеспечить минимум возрастания затрат при уменьшении Ткр.
Алгоритм заключается в следующем:
1. Найти критический путь, его длину Ткр и соответствующую ему суммарную стоимость
С = ∑C(ij)
Lкр = (i0, i1...,in„) из предположения t(ij) = tmax(ij)
На этом пути найти работу (kl)єLкр, у которой S(kl) будет иметь наименьшее значение.
Для выбранной работы найти величину ∆t(kl) = tmax(kl) - tmin(ki)
Определить ∆С(кl) = S(ki)*∆t(kl)
Следовательно, при уменьшении Ткр на величину ∆t(kl) стоимость всех работ увеличивается на величину ∆С(кl)
С = СПред. + ∆С(кl)
Рассчитать сетевую модель с учетом измененной продолжительности работы (кl).
Возвратиться к п.1. В результате реализации данного алгоритма получается график зависимости С от Ткр. По этому графику легко координировать отношения между инвестором и производителем.
5. Ленточный график Ганта.
Первой попыткой наглядно отразить последовательность и ход работ были ленточные графики Ганта