
- •Введение
- •Энергокинематический расчет
- •Определение общего передаточного отношения и разбивка его по ступеням
- •Определение общего кпд привода
- •Определение угловых скоростей валов. Расчет мощностей и крутящих моментов на валах I, II и III.
- •Расчет цилиндрической косозубой передачи.
- •Проектировочный расчет передачи по контактной выносливости.
- •Проверочный расчет зубьев на контактную выносливость.
- •Проверочный расчет зубьев на изгибную выносливость.
- •Расчет цилиндрической прямозубой передачи
- •Расчёт и проектирование промежуточного вала на опорах качения
- •Проектировочный расчёт вала
- •Определение наиболее опасного сечения вала
- •Выбор и проверочный расчет подшипников качения
- •Уточнённый проверочный расчет промежуточного вала
- •Проверка на прочность шпоночных соединений
- •Проверочный расчёт зубьев при перегрузках
- •Список литературы
Проверочный расчет зубьев на изгибную выносливость.
Задачей этого пункта является проверка зубьев шестерни и колеса на изгибную выносливость. Основной вид разрушения – усталостная поломка зуба.
Условие изгибной выносливости зубьев:
 ,
,
где F и [F] – расчетное и допустимое напряжение на изгиб.
Определим значения сил, действующих в зацеплении.
Окружная:

Радиальная:

Осевая:

Проверяем зубья на выносливость по напряжениям изгиба:
 ,
[1, с.46]
,
[1, с.46]
где KF – коэффициент нагрузки, KF= KF* KFV;
KF - коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (коэффициент концентрации нагрузки), KF =1.23 [1, табл.3.7, с.43];
KFV – коэффициент динамичности, KFV =1.4 [1, табл. 3.8, с.43].
Тогда
 .
.
YF – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев Zv1.
а)
для шестерни
 ;
;
б)
для колеса
 .
.
Тогда YF1=3.76; YF2=3.60 [1, с.42].
Определяем коэффициент компенсации погрешности Y и коэффициент, учитывающий неравномерность распределения нагрузки между зубьями KF.
 ,
[1, с.46]
,
[1, с.46]
 ,
[1, с.47]
,
[1, с.47]
где n – степень точности;
- коэффициент торцевого перекрытия, =1,5 [1, с.47]
Допускаемое напряжение:
 ,
[1, с.43],
,
[1, с.43],
где
 –
предел выносливости при отнулевом цикле
изгиба. Для стали 40Х улучшенной при
твердости НВ<350
=1,8НВ
[1, табл. 3.9, с.44-45];
–
предел выносливости при отнулевом цикле
изгиба. Для стали 40Х улучшенной при
твердости НВ<350
=1,8НВ
[1, табл. 3.9, с.44-45];
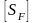 -
коэффициент безопасности,
-
коэффициент безопасности,
 .
.
Здесь
 - коэффициент, учитывающий нестабильность
свойств материала зубчатых колес,
=1.75
[1, табл. 3.9, с.44-45];
- коэффициент, учитывающий нестабильность
свойств материала зубчатых колес,
=1.75
[1, табл. 3.9, с.44-45];
 - коэффициент, учитывающий способ
получения заготовки зубчатого колеса,
=1
для поковок и штамповок [1, с.44].
- коэффициент, учитывающий способ
получения заготовки зубчатого колеса,
=1
для поковок и штамповок [1, с.44].
а)
для шестерни
 .
.
б)
для колеса
 .
.
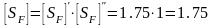 .
.
Допускаемые напряжения:
а) для шестерни
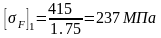
б) для колеса

Проверку
на изгиб следует проводить для того
зубчатого колеса, для которого отношение
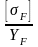 меньше.
меньше.
а) для шестерни

б) для колеса
 .
.
Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше. Тогда:
 Условие
прочности зубьев на изгибную выносливость
выполнено.
Условие
прочности зубьев на изгибную выносливость
выполнено.
Расчет цилиндрической прямозубой передачи
По
условию
 .
.
Принимаем для прямозубых передач коэффициент ширины венца по межосевому расстоянию ψba = 0.3 [1, с. 33].
Коэффициент ширины шестерни по диаметру:
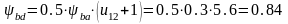 [1,
с. 33].
[1,
с. 33].
Ширина шестерни будет равна:
 .
.
Примем
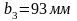 согласно ряду нормальных линейных
размеров.
согласно ряду нормальных линейных
размеров.
Коэффициент
ширины венца шестерни по модулю примем
 .
Тогда модуль будет равен:
.
Тогда модуль будет равен:
 .
.
Выберем
модуль из ряда рекомендованных значений.
Окончательно примем
 .
.
Определим число зубьев шестерни:
 .
.
Принимаем
 .
.
Найдем диаметры вершин и впадин зубьев шестерни:
 .
.
Расчёт и проектирование промежуточного вала на опорах качения
Проектировочный расчёт вала
Задача: предварительное определение минимального диаметра вала.
Допущения: считаем, что вал гладкий, круглый стержень, испытывающий только статическое кручение.
Определим диаметр вала [1,с.161]:
 ,
,
где
 - допускаемое напряжение на кручение,
- допускаемое напряжение на кручение,
 [1,с.161].
[1,с.161].
Тогда получим
 .
.
Значение
dB
округлим в большую сторону до значения
из стандартного ряда
 .
.
Т.о. принимаем окончательно диаметр вала .
Исходя
из значения
 ,
принимаем диаметр вала под подшипник
,
принимаем диаметр вала под подшипник
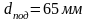 .
Принимаем диаметр бурта для упора
подшипника и ступицы зубчатого колеса
.
Принимаем диаметр бурта для упора
подшипника и ступицы зубчатого колеса
 .
Принимаем диаметр под ступицей зубчатого
колеса
.
Принимаем диаметр под ступицей зубчатого
колеса
 ,
а диаметр под уплотнением
,
а диаметр под уплотнением
 .
.
Изобразим конструкцию промежуточного вала:
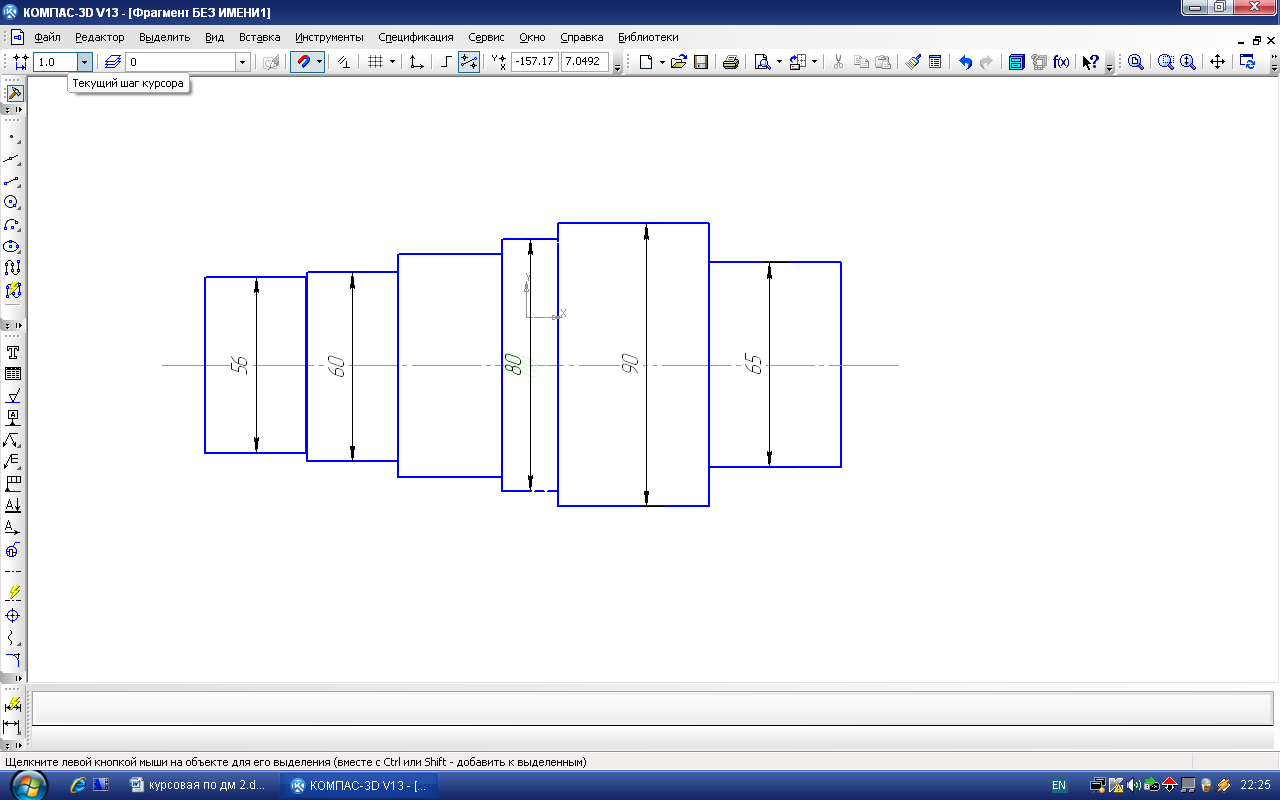
Рисунок 3. Конструкция промежуточного вала
