22.ФормулаТейлора

Пусть f(x)определена на (a;b).пусть х0∈(a;b).Пусть f(x) имеет в х0 n производных. Тогда ф.мб представлена

где 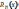- остаточный член формулы Тейлора:

23.Монотонные ф.Теоремы о ф.,непрерывных на отрезках

f(x) определена на [a;b]

f(x)непрерывна и диф-ма на [a;b] Для того,что бы на [a;b] ф возрастала(убывала)достаточно f’(x)>0(f’(x)<0)

док-во.Предположим f(x)<0.расм.a<x1<x2<b∈[a;b]

в силу т.лагранжа f(x2)-f(x2)=f’(ƞ)(x2-x1),где ƞ∈ [x1;x2].предположим f’(x)>0,тогда возрастает.

F(x2)-f(x1)>0=>f(x2)≥f(x1)

Опред:точка х0-т.строго локального максимума(мин.)если для любого x∈[x0-δ;. x0+δ] выполняется неравенство F(x)<f(x0) (f(x)>f(x0)

24. Экстремум функции

Значение f(x₀) называется локальным максимумом (локальным минимумом) функции y=f(x), если при любом достаточно малом δ выполняется условие f(x₀)>f(x) (f(x₀)<f(x)) ∀x∈(x₀-δ) ∪(x₀+δ). Точка x₀ называется точкой максимума (минимума) функции. Локальные максимумы и минимумы функции называются экстремумами функции, а точки максимума и минимума – точками экстремума.

Теорема (необходимое условие локального экстремума). Если функция y=f(x) имеет в точке x₀ локальный экстремум, то производная f’(x)обращается в 0 или не существует.

Док-во. Т.к х0-т.экстремума,то в (x₀+δ; x₀-δ) она является т. max и min.Тогда по т.Ферма f’(x)=0.Замеч.если f’(x)=0 это не значит,что х-эксремум.

Теорема (первое достаточное условие экстремума). Пусть x₀ – критическая точка функции y=f(x); если при переходе через точку x₀ слева направо производная f'(x) меняет знак с плюса на минус (с минуса на плюс), то функция f(x) в точке x₀ имеет локальный максимум (локальный минимум);если же производная f’(x) не меняет знака в δ-окрестности точки x₀, то данная функция не имеет в точке x₀ локального экстремума.

Теорема (второе достаточное условие). Пусть f'(x₀)=0 и f’’(x₀)≠0, тогда функция y=f(x) в точке x₀ имеет экстремум, причем x₀ – точка локального максимума (минимума), если f’’(x₀)<0 (f’’(x₀)<0).

23. Экстремум функции. Необходимые и достаточные условия существования

Значение f(x0) называется локальным максимумом (локальным минимумом) функции y=f(x), если при любом достаточно малом δ выполняется условие f(x0)>f(x) (f(x0)<f(x)) ∀x∈(x0- δ) ∪(x0+ δ). Точка x0 называется точкой максимума (минимума) функции. Локальные максимумы и минимумы функции называются экстремумами функции, а точки максимума и минимума – точками экстремума.

Теорема (необходимое условие локального экстремума). Если функция y=f(x) имеет в точке x0 локальный экстремум, то производная f’(x)обращается в 0 или не существует.

Точки, в которых f'(x)=0 или f'(x) не существует, называются критическими. Экстремум в таких точках может быть, а может и не быть.

Теорема (первое достаточное условие экстремума). Пусть x0 – критическая точка функции y=f(x); если при переходе через точку x0 слева направо производная f'(x) меняет знак с плюса на минус (с минуса на плюс), то функция f(x) в точке x0 имеет локальный максимум (локальный минимум);если же производная f’(x) не меняет знака в δ-окрестности точки x0, то данная функция не имеет в точке x0 локального экстремума.

Теорема (второе достаточное условие). Пусть f'(x0)=0 и f’’(x0)≠0, тогда функция y=f(x) в точке x0 имеет экстремум, причем x0 – точка локального максимума (минимума), если f’’(x0)<0 (f’’(x0)<0).