59.Особенности вычисления определен.Интегралов

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x₀ < x₁ < x₂ < x_n = b Тогда говорят, что произведено разбиение R отрезка [a;b] Далее выберем произв. точку  , i = 0, Определённым интегралом от функцииf(x) на отрезке [a;b]называется предел интегральных сумм Θ_R при  , если он существует независимо от разбиения R и выбора точек ξ_i, т.е.   (1) Если существует (1), то функция f(x) называется интегрируемой на[a;b] – определение интеграла по Риману.

Определение интеграла на языке  , δ:(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx

Определённый интеграл   численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

60. Площадь плоской фигуры

 а) Допустим, что фигура предполагает наличие границы

является криволинейной трапецией и , при условии, что на

Если находится ниже оси (рис. 18.1), то  

б) Предположим, что для фигуры харакерно наличие границы Площадь (рис. 18.2, а),

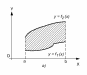
 соответственно получаем формулу В общем случае площадь находится с помощью формулы

61. Вычисление площади поверхности тела вращения

 Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

  Разобьем дугу АВ на n частей точками M₀, M₁, M₂, … , M_n. Координаты вершин полученной ломаной имеют координаты x_i и y_i. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна P_i. Эта площадь может быть найдена по формуле:

Здесь S_i – длина каждой хорды.

Применяем теорему Лагранжа к отношению  .

Получаем: 

Тогда 

  

Площадь поверхности, описанной ломаной равна:

Эта сумма не является интегральной, но можно показать, что

Тогда   - формула вычисления площади поверхности тела вращения.

62. Вычисление объема тела вращения

Объем тела вращения равен 

Придадим x приращение Δx > 0 (x + Δx < b). Построим два цилиндра с общей высотой Δx (рис. 7.2.2). Меньший цилиндр имеет своим основанием круг площадью S (x), а больший – круг площадью S (x + Δx). Если ΔV – прирост объема тела вращения, то S (x)Δx < ΔV < S (x + Δx)Δx, откуда 

Поскольку функция f (x) непрерывна, то непрерывна и функция 

следовательно, 

Переходя к пределу в двойном неравенстве, имеем 

то есть V' (x) = S (x).

Объем V (x) является первообразной для функции S (x) на промежутке [a; b]. Отсюда имеем