35 Вопрос. Графовые модели программ, их взаимосвязь. Граф алгоритма. Критический путь графа алгоритма.

{Вадик: критический путь графа алгоритма, насколько я понял, это длина самого длинного пути от "входа" графа к его "выходу" (от первого оператора к последнему) В случае канонической ЯПФ графа длина критического пути на единицу меньше высоты канонической ЯПФ.}

Рассмотрим 4 основные Графовые модели программ: граф управления программы (ГУ),

информационный граф программы (ИГ), операционная история (ОИ), информационная

история (ИИ).

Пример:

1 y=b1-a1

2 x=y

3 DO i = 2, n

4 x = (bi – ci*x)/ai

5 if (x<y) goto 7

6 y=x

7 END DO

Граф управления. Каждому оператору исходной программы поставим в

соответствие вершину графа — экземпляр преобразователя или распознавателя в

зависимости от типа оператора. Получим множество вершин, между которыми согласно

исходной программе определим отношение, соответствующее передаче управления. Если

текст программы допускает выполнение одного оператора непосредственно за другим, то

соответствующие вершины соединим дугой, направленной от предшественника к

последователю. Его основным свойством является независимость от входных данных

программы. Множества вершин и дуг для каждой программы фиксированы и образуют

единственный граф.

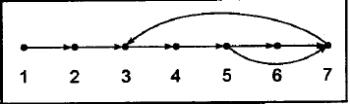
Информационный граф. Изменим графовую основу. Будем среди операторов

принимать во внимание только преобразователи, а в качестве отношения между ними

брать отношение информационной зависимости. Построим сначала граф, в котором вер-

шины соответствуют операторам-преобразователям. Две вершины соединим

информационной дугой, если между какими-нибудь срабатываниями соответствующих

операторов теоретически возможна информационная связь. Информационный граф

не зависит от входных данных. В нем могут быть "лишние" дуги, которые не реализуются

либо при конкретных входных данных, либо совместно с другими дугами.

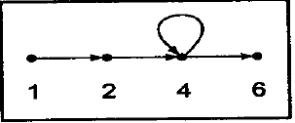
Операционная история. Теперь предположим, что каким-то образом мы

определили начальные данные программы и наблюдаем за ее выполнением на обычном

последовательном вычислителе. Каждое срабатывание каждого оператора (а оно не-

обязательно будет единственным) будем фиксировать отдельной вершиной. Получим

множество, которое количественно почти всегда будет отличаться от множества вершин

графа управления. В данном случае порядок непосредственного срабатывания операторов

можно определить точно. Соединяем вершины дугами передач управления, получаем

ориентированный граф. Этот граф представляет единственный путь от начальной

вершины к конечной. По существу это не что иное, как последовательность срабатывания

преобразователей и распознавателей исходной программы при заданных входных данных.

В операционной истории от входных данных зависит практически все: общее число

вершин, количество вершин, соответствующих одному оператору, и даже набор

присутствующих преобразователей и распознавателей. Для графа управления. Всегда линейный.

Информационная история. Снова каким-то образом определим начальные

данные программы и будем наблюдать за ее выполнением на последовательном

вычислителе. Каждое срабатывание каждого оператора-преобразователя будем

фиксировать отдельной вершиной. Соединим вершины дугами передач информации,

получим ориентированный граф. Для информационного графа. Может быть без дуг (1).

Граф алгоритма. Пусть при фиксированных входных данных программа описывает некоторый алгоритм. Построим ориентированный граф. В качестве вершин возьмем любое множество, например, множество точек арифметического пространства, на которое

взаимнооднозначно отображается множество всех операций алгоритма. Возьмем любую

пару вершин и, v. Допустим, что согласно описанному выше частичному порядку

операция, соответствующая вершине и, должна поставлять аргумент операции,

соответствующей вершине v. Тогда проведем дугу из вершины и в вершину v. Если

соответствующие операции могут выполняться независимо друг от друга, дугу проводить

не будем. В случае, когда аргументом операции является начальное данное или результат

операции нигде не используется, возможны различные договоренности. Например, можно

считать, что соответствующие дуги отсутствуют. Мы будем поступать в зависимости от

обстоятельств. Ориентированный ациклический мультиграф.

Независимо от способа построения ориентированного графа, те его вершины, которые не

имеют ни одной входящей или выходящей дуги, будем называть соответственно

входными или выходными вершинами графа.