Моделирование и анализ предлагаемой сау
РЕЗУЛЬТАТЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ
ОДНОКОНТУРНОЙ ЦИФРОВОЙ АВТОМАТИЧЕСКОЙ СИСТЕМЫ
01.01.2012
********************************************************************
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :
K * Exp(-Tau*P)
W(P) = ----------------- .
P
ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :
Коэффициент передачи K = 0.100
Запаздывание Tau = 17.600
********************************************************************
ПАРАМЕТРЫ ЭЛЕМЕНТОВ СИСТЕМЫ :
Коэффициент передачи датчика 1.000
Коэффициент передачи испол.устройства 1.000
Коэффициент передачи регулирующего органа 1.000
ДИСКРЕТНОСТЬ РАБОТЫ СИСТЕМЫ 3.000
СТЕПЕНЬ КОЛЕБАТЕЛЬНОСТИ M = 0.90
ЛИНИЯ РАВНОГО ЗАПАСА УСТОЙЧИВОСТИ ЗАДАЕТСЯ В ВИДЕ ТАБЛИЦЫ
----------------------------------------
K1 | K2
----------------------------------------
0.03780 | 0.03756
0.07311 | 0.07224
0.10585 | 0.10405
0.13593 | 0.13301
0.16332 | 0.15916
0.18799 | 0.18256
0.20993 | 0.20328
0.22915 | 0.22138
0.24569 | 0.23696
0.25958 | 0.25011
0.27089 | 0.26092
0.27969 | 0.26950
0.28605 | 0.27595
0.29006 | 0.28040
0.29183 | 0.28294
0.29146 | 0.28371
0.28906 | 0.28280
0.28475 | 0.28035
0.27864 | 0.27645
0.27087 | 0.27124
----------------------------------------
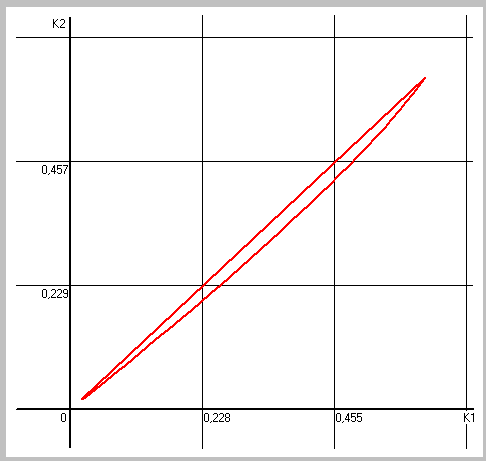
Рис. 26 Линия равного запаса устойчивости
********************************************************************
РЕКОМЕНДУЕМЫЕ ПАРАМЕТРЫ РЕГУЛЯТОРА :
-------------------------------
НАСТРОЙКА - K1 = 0.2919
НАСТРОЙКА - K2 = 0.2836
-------------------------------
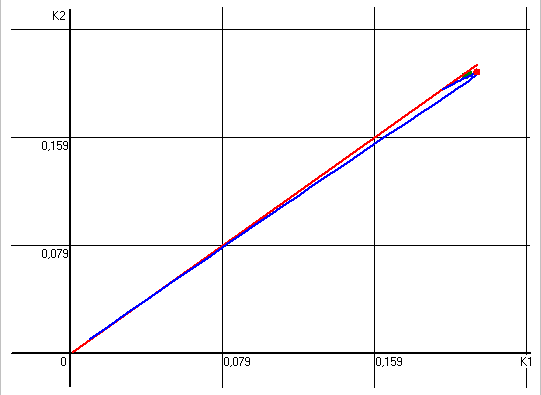
Рис. 28 Настройки регултора
ПЕРЕХОДНЫЙ ПРОЦЕСС ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ
Задающее воздействие ступенчатое = 10.0000
********************************************************************
П И - З А К О Н РЕГУЛИРОВАНИЯ
Выбранные параметры закона :
Настройка К1 = 0.2881
Настройка К2 = 0.2848
********************************************************************
Такт Задание Рег орган Система Ср.кв.ош
0 10,0000 2,8813 0,0000 100,0000
1 10,0000 2,9143 0,0000 100,0000
2 10,0000 2,9472 0,0000 100,0000
3 10,0000 2,9802 0,0000 100,0000
4 10,0000 3,0131 0,0000 100,0000
5 10,0000 3,0461 0,0000 100,0000
6 10,0000 3,0791 0,0000 100,0000
7 10,0000 3,1120 0,8644 100,0000
8 10,0000 2,8960 1,7387 98,1622
9 10,0000 2,6742 2,6228 95,1709
10 10,0000 2,4467 3,5169 91,4665
11 10,0000 2,2134 4,4208 87,3469
12 10,0000 1,9743 5,3347 83,0223
13 10,0000 1,7294 6,2584 78,6468
14 10,0000 1,4786 7,1920 74,3370
15 10,0000 1,2219 8,0608 70,1837
16 10,0000 0,9809 8,8630 66,2765
17 10,0000 0,7561 9,5970 62,6663
18 10,0000 0,5484 10,2610 59,3766
19 10,0000 0,3584 10,8533 56,4112
20 10,0000 0,1869 11,3721 53,7596
21 10,0000 0,0346 11,8157 51,4016
22 10,0000 -0,0978 12,1823 49,3101
23 10,0000 -0,2094 12,4766 47,4539
24 10,0000 -0,3013 12,7034 45,8011
25 10,0000 -0,3749 12,8679 44,3206
26 10,0000 -0,4312 12,9754 42,9837
27 10,0000 -0,4716 13,0315 41,7648
28 10,0000 -0,4976 13,0419 40,6415
29 10,0000 -0,5106 13,0125 39,5952
30 10,0000 -0,5121 12,9497 38,6107
31 10,0000 -0,5040 12,8593 37,6760
32 10,0000 -0,4876 12,7469 36,7821
33 10,0000 -0,4647 12,6175 35,9222
34 10,0000 -0,4365 12,4760 35,0916
35 10,0000 -0,4043 12,3268 34,2871
36 10,0000 -0,3695 12,1736 33,5068
37 10,0000 -0,3330 12,0199 32,7493
38 10,0000 -0,2959 11,8688 32,0142
39 10,0000 -0,2590 11,7225 31,3012
40 10,0000 -0,2230 11,5831 30,6101
41 10,0000 -0,1885 11,4521 29,9409
42 10,0000 -0,1560 11,3308 29,2937
43 10,0000 -0,1259 11,2200 28,6682
44 10,0000 -0,0983 11,1201 28,0642
45 10,0000 -0,0735 11,0313 27,4814
46 10,0000 -0,0517 10,9536 26,9193
47 10,0000 -0,0327 10,8867 26,3774
48 10,0000 -0,0165 10,8302 25,8551
49 10,0000 -0,0032 10,7834 25,3518
50 10,0000 0,0076 10,7456 24,8668
51 10,0000 0,0159 10,7161 24,3992
52 10,0000 0,0219 10,6940 23,9486
53 10,0000 0,0259 10,6785 23,5140
54 10,0000 0,0281 10,6687 23,0948
55 10,0000 0,0287 10,6638 22,6904
56 10,0000 0,0279 10,6628 22,3001
57 10,0000 0,0260 10,6651 21,9231
58 10,0000 0,0232 10,6699 21,5591
59 10,0000 0,0196 10,6765 21,2072
60 10,0000 0,0155 10,6842 20,8671
61 10,0000 0,0110 10,6927 20,5381
62 10,0000 0,0063 10,7013 20,2197
63 10,0000 0,0016 10,7096 19,9114
64 10,0000 -0,0032 10,7174 19,6128
65 10,0000 -0,0077 10,7244 19,3235
66 10,0000 -0,0121 10,7303 19,0429
67 10,0000 -0,0162 10,7349 18,7707
68 10,0000 -0,0199 10,7382 18,5065
69 10,0000 -0,0233 10,7401 18,2499
70 10,0000 -0,0263 10,7406 18,0006
71 10,0000 -0,0289 10,7396 17,7582
72 10,0000 -0,0310 10,7373 17,5224
73 10,0000 -0,0328 10,7337 17,2930
74 10,0000 -0,0342 10,7288 17,0696
75 10,0000 -0,0352 10,7228 16,8520
76 10,0000 -0,0359 10,7158 16,6399
77 10,0000 -0,0363 10,7079 16,4331
78 10,0000 -0,0363 10,6993 16,2315
79 10,0000 -0,0362 10,6900 16,0347
80 10,0000 -0,0358 10,6801 15,8426
81 10,0000 -0,0352 10,6699 15,6550
82 10,0000 -0,0345 10,6593 15,4718
83 10,0000 -0,0337 10,6485 15,2928
84 10,0000 -0,0328 10,6377 15,1178
85 10,0000 -0,0318 10,6268 14,9468
86 10,0000 -0,0307 10,6159 14,7795
87 10,0000 -0,0297 10,6052 14,6159
88 10,0000 -0,0286 10,5946 14,4557
89 10,0000 -0,0276 10,5842 14,2991
90 10,0000 -0,0265 10,5741 14,1457
91 10,0000 -0,0255 10,5643 13,9955
92 10,0000 -0,0246 10,5548 13,8484
93 10,0000 -0,0237 10,5456 13,7044
94 10,0000 -0,0229 10,5367 13,5633
95 10,0000 -0,0221 10,5281 13,4250
96 10,0000 -0,0214 10,5198 13,2894
97 10,0000 -0,0208 10,5118 13,1566
98 10,0000 -0,0202 10,5042 13,0264
99 10,0000 -0,0197 10,4968 12,8986
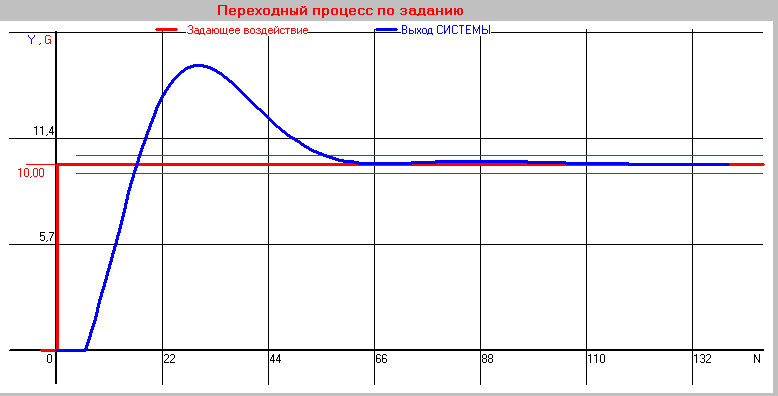
Рис. 29 Переходный процесс по заданию
Приложение
АППРОКСИМАЦИЯ РАЗГОННОЙ КРИВОЙ
МЕТОДОМ МОМЕНТОВ ПЕРЕХОДНОЙ ФУНКЦИИ ПО КАНАЛУ ВОЗМУЩЕНИЯ
ПАРАМЕТРЫ ВХОДНОГО ВОЗДЕЙСТВИЯ :
ЗНАЧЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ ДО ЭКСПЕРИМЕНТА = 38.000
ЗНАЧЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ В ИМПУЛЬСЕ = 43.000
ДЛИТЕЛЬНОСТЬ ИМПУЛЬСА = 36.000
ПАРАМЕТРЫ ВЫХОДНОГО СИГНАЛА ОБЪЕКТА :
СРЕДНЕЕ ЗНАЧЕНИЕ ВЫХОДНОГО СИГНАЛА ДО ОПЫТА = 10.000
УСТАНОВИВШЕЕСЯ СРЕДНЕЕ ЗНАЧЕНИЕ ПЕРВЫХ РАЗНОСТЕЙ = 0.500
ШАГ ДИСКРЕТНОСТИ ПО ВРЕМЕНИ = 1.000
ЧИСЛО ТОЧЕК КРИВОЙ РАЗГОНА = 40
КРИВАЯ РАЗГОНА
Номер точки Значение кривой разгона
1 10.000
2 9.750
3 9.500
4 9.250
5 9.000
6 8.750
7 8.500
8 8.250
9 8.000
10 7.800
11 8.000
12 8.250
13 8.500
14 8.750
15 9.000
16 9.500
17 9.750
18 10.000
19 10.500
20 11.000
21 11.500
22 12.000
23 12.500
24 13.000
25 13.500
26 14.000
27 14.500
28 15.000
29 15.500
30 16.000
31 16.500
32 17.000
33 17.500
34 18.000
35 18.500
36 19.000
37 19.500
38 20.000
39 20.500
40 21.000
**********************************************************************
МОДЕЛЬ С М И Н И М А Л Ь Н Ы М
ЗНАЧЕНИЕМ ДИСПЕРСИИ АДЕКВАТНОСТИ
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ
K * Exp(-Tau*P)
W(P) = ----------------- .
P
ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :
Коэффициент передачи K = -0.100
Запаздывание Tau = 17.596
НОРМИРОВАННЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ОБЪЕКТА И МОДЕЛИ
Врем Объект Модель
0.000 0.000 0.000
1.000 -0.500 0.000
2.000 -1.000 0.000
3.000 -1.500 0.000
4.000 -2.000 0.000
5.000 -2.500 0.000
6.000 -3.000 0.000
7.000 -3.500 0.000
8.000 -4.000 0.000
9.000 -4.400 0.000
10.000 -4.000 0.000
11.000 -3.500 0.000
12.000 -3.000 0.000
13.000 -2.500 0.000
14.000 -2.000 0.000
15.000 -1.000 0.000
16.000 -0.500 0.000
17.000 0.000 0.000
18.000 1.000 0.404
19.000 2.000 1.404
20.000 3.000 2.404
21.000 4.000 3.404
22.000 5.000 4.404
23.000 6.000 5.404
24.000 7.000 6.404
25.000 8.000 7.404
26.000 9.000 8.404
27.000 10.000 9.404
28.000 11.000 10.404
29.000 12.000 11.404
30.000 13.000 12.404
31.000 14.000 13.404
32.000 15.000 14.404
33.000 16.000 15.404
34.000 17.000 16.404
35.000 18.000 17.404
36.000 19.000 18.404
ДИСПЕРСИЯ АДЕКВАТНОСТИ ДАННОЙ МОДЕЛИ = 3.496169
**********************************************************************
В Ы Б О Р О Ч Н А Я МОДЕЛЬ
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ
K * Exp(-Tau*P)
W(P) = ----------------- .
P
ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :
Коэффициент передачи K = -0.100
Запаздывание Tau = 17.596
НОРМИРОВАННЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ОБЪЕКТА И МОДЕЛИ
Врем Объект Модель
0.000 0.000 0.000
1.000 -0.500 0.000
2.000 -1.000 0.000
3.000 -1.500 0.000
4.000 -2.000 0.000
5.000 -2.500 0.000
6.000 -3.000 0.000
7.000 -3.500 0.000
8.000 -4.000 0.000
9.000 -4.400 0.000
10.000 -4.000 0.000
11.000 -3.500 0.000
12.000 -3.000 0.000
13.000 -2.500 0.000
14.000 -2.000 0.000
15.000 -1.000 0.000
16.000 -0.500 0.000
17.000 0.000 0.000
18.000 1.000 0.404
19.000 2.000 1.404
20.000 3.000 2.404
21.000 4.000 3.404
22.000 5.000 4.404
23.000 6.000 5.404
24.000 7.000 6.404
25.000 8.000 7.404
26.000 9.000 8.404
27.000 10.000 9.404
28.000 11.000 10.404
29.000 12.000 11.404
30.000 13.000 12.404
31.000 14.000 13.404
32.000 15.000 14.404
33.000 16.000 15.404
34.000 17.000 16.404
35.000 18.000 17.404
36.000 19.000 18.404
ДИСПЕРСИЯ АДЕКВАТНОСТИ ДАННОЙ МОДЕЛИ = 3.496169
**********************************************************************
АППРОКСИМАЦИЯ РАЗГОННОЙ КРИВОЙ
МЕТОДОМ МОМЕНТОВ ПЕРЕХОДНОЙ ФУНКЦИИ ПО КАНАЛУ УПРАВЛЕНИЯ
01.01.2002
ПАРАМЕТРЫ ВХОДНОГО ВОЗДЕЙСТВИЯ :
ЗНАЧЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ ДО ЭКСПЕРИМЕНТА = 35.000
ЗНАЧЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ В ИМПУЛЬСЕ = 40.000
ДЛИТЕЛЬНОСТЬ ИМПУЛЬСА = 36.000
ПАРАМЕТРЫ ВЫХОДНОГО СИГНАЛА ОБЪЕКТА :
СРЕДНЕЕ ЗНАЧЕНИЕ ВЫХОДНОГО СИГНАЛА ДО ОПЫТА = 10.000
УСТАНОВИВШЕЕСЯ СРЕДНЕЕ ЗНАЧЕНИЕ ПЕРВЫХ РАЗНОСТЕЙ = -0.500
ШАГ ДИСКРЕТНОСТИ ПО ВРЕМЕНИ = 1.000
ЧИСЛО ТОЧЕК КРИВОЙ РАЗГОНА = 40
КРИВАЯ РАЗГОНА
Номер точки Значение кривой разгона
1 10.000
2 10.500
3 11.000
4 11.500
5 12.000
6 12.500
7 13.000
8 13.500
9 14.000
10 14.500
11 15.000
12 15.200
13 15.500
14 15.200
15 15.000
16 14.500
17 14.000
18 13.500
19 13.000
20 12.500
21 12.000
22 11.500
23 11.000
24 10.500
25 10.000
26 9.500
27 9.000
28 8.500
29 8.000
30 7.500
31 7.000
32 6.500
33 6.000
34 5.500
35 5.000
36 4.500
37 4.000
38 3.500
39 3.000
40 2.500
**********************************************************************
МОДЕЛЬ С М И Н И М А Л Ь Н Ы М
ЗНАЧЕНИЕМ ДИСПЕРСИИ АДЕКВАТНОСТИ
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ
K * Exp(-Tau*P)
W(P) = ----------------- .
P
ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :
Коэффициент передачи K = 0.100
Запаздывание Tau = 24.692
НОРМИРОВАННЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ОБЪЕКТА И МОДЕЛИ
Врем Объект Модель
0.000 -0.000 0.000
1.000 -1.000 0.000
2.000 -2.000 0.000
3.000 -3.000 0.000
4.000 -4.000 0.000
5.000 -5.000 0.000
6.000 -6.000 0.000
7.000 -7.000 0.000
8.000 -8.000 0.000
9.000 -9.000 0.000
10.000 -10.000 0.000
11.000 -10.400 0.000
12.000 -11.000 0.000
13.000 -10.400 0.000
14.000 -10.000 0.000
15.000 -9.000 0.000
16.000 -8.000 0.000
17.000 -7.000 0.000
18.000 -6.000 0.000
19.000 -5.000 0.000
20.000 -4.000 0.000
21.000 -3.000 0.000
22.000 -2.000 0.000
23.000 -1.000 0.000
24.000 -0.000 0.000
25.000 1.000 0.308
26.000 2.000 1.308
27.000 3.000 2.308
28.000 4.000 3.308
29.000 5.000 4.308
30.000 6.000 5.308
31.000 7.000 6.308
32.000 8.000 7.308
33.000 9.000 8.308
34.000 10.000 9.308
35.000 11.000 10.308
36.000 12.000 11.308
ДИСПЕРСИЯ АДЕКВАТНОСТИ ДАННОЙ МОДЕЛИ = 30.918631
**********************************************************************
В Ы Б О Р О Ч Н А Я МОДЕЛЬ
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ
K * Exp(-Tau*P)
W(P) = ----------------- .
P
ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :
Коэффициент передачи K = -0.100
Запаздывание Tau = 24.692
НОРМИРОВАННЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ОБЪЕКТА И МОДЕЛИ
Врем Объект Модель
0.000 -0.000 0.000
1.000 -1.000 0.000
2.000 -2.000 0.000
3.000 -3.000 0.000
4.000 -4.000 0.000
5.000 -5.000 0.000
6.000 -6.000 0.000
7.000 -7.000 0.000
8.000 -8.000 0.000
9.000 -9.000 0.000
10.000 -10.000 0.000
11.000 -10.400 0.000
12.000 -11.000 0.000
13.000 -10.400 0.000
14.000 -10.000 0.000
15.000 -9.000 0.000
16.000 -8.000 0.000
17.000 -7.000 0.000
18.000 -6.000 0.000
19.000 -5.000 0.000
20.000 -4.000 0.000
21.000 -3.000 0.000
22.000 -2.000 0.000
23.000 -1.000 0.000
24.000 -0.000 0.000
25.000 1.000 0.308
26.000 2.000 1.308
27.000 3.000 2.308
28.000 4.000 3.308
29.000 5.000 4.308
30.000 6.000 5.308
31.000 7.000 6.308
32.000 8.000 7.308
33.000 9.000 8.308
34.000 10.000 9.308
35.000 11.000 10.308
36.000 12.000 11.308
ДИСПЕРСИЯ АДЕКВАТНОСТИ ДАННОЙ МОДЕЛИ = 30.918631