Задание.

Составить технологическую схему и карту сборки (разборки) механизма, а также краткое описание его работы и спецификацию по рабочему чертежу.

Порядок оформления отчета

Отчет о практической работе оформляется на белой бумаге формата А4 с одной или обеих сторон. Правила оформления отчета изложены в методических указаниях к оформлению расчетно-проектных, расчетно-графических работ, курсовых и дипломных проектов 15].

Отчет включает в себя следующие разделы:

• цель работы;

• теоретическую часть, в которой приводятся характеристика основных ремонтных операций, методы технологии ремонта и правила составления технологической схемы и карты сборки (разборки) сборочных единиц;

• графическую часть, выполненную в соответствии с требованиями ЕСКД и включающую краткое описание работы механизма, рабочий чертеж которого указан в варианте, спецификацию к нему, технологическую схему и карту сборки или разборки.

Контрольные вопросы

1. Перечислите основные ремонтные операции.

2. Охарактеризуйте методы технологии ремонта.

3. Приведите классификацию соединения деталей сборочных единиц.

4. Поясните порядок составления технологической документации ремонтных работ на сборочные операции.

5. Как осуществляется контроль качества общей сборки отремонтированного оборудования?

Таблица 3.1

Варианты заданий

Номер варианта	Название сборочной единицы
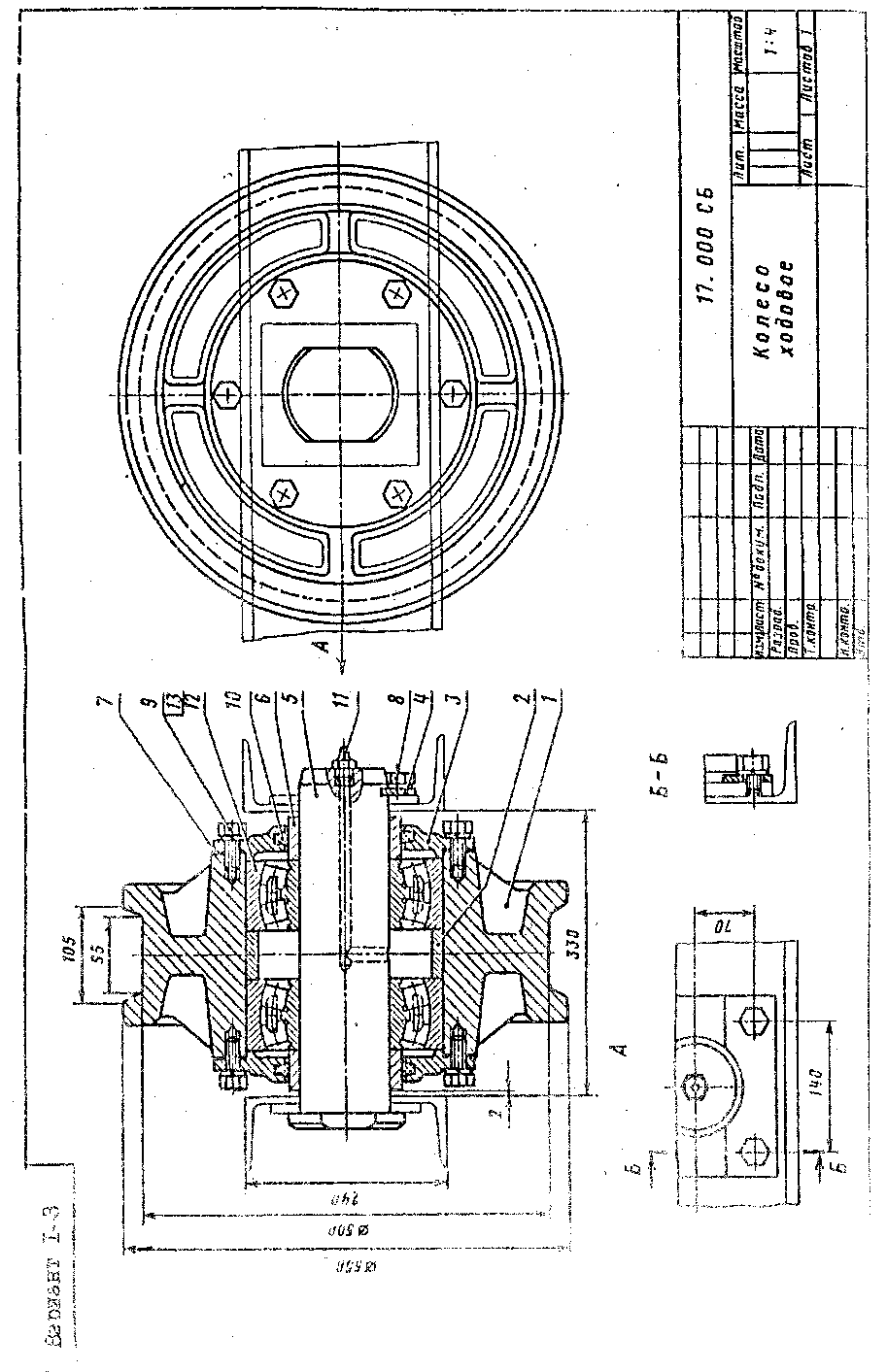
1 2 3	Колесо ходовое
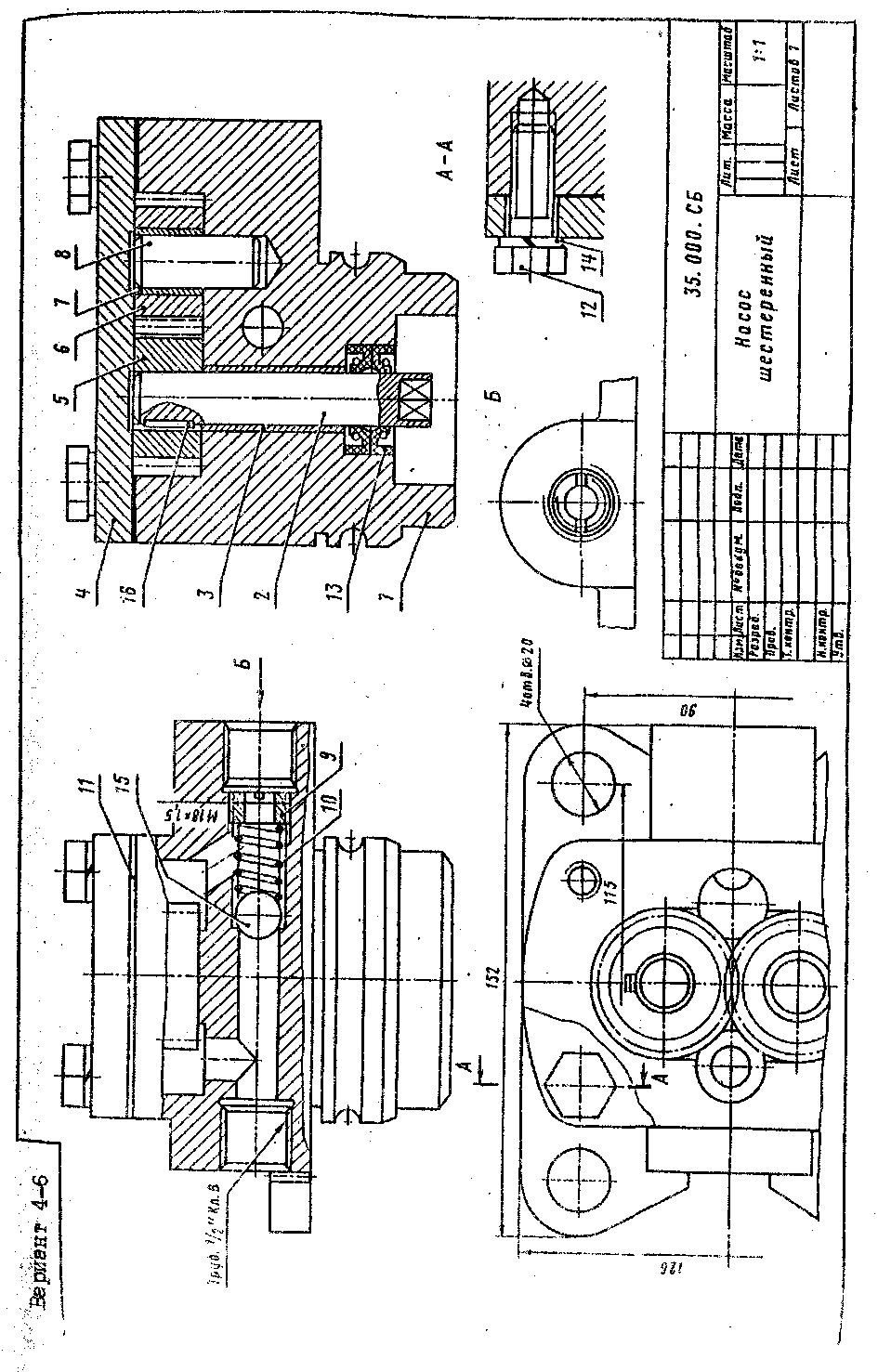
4 5 6	Насос шестеренный
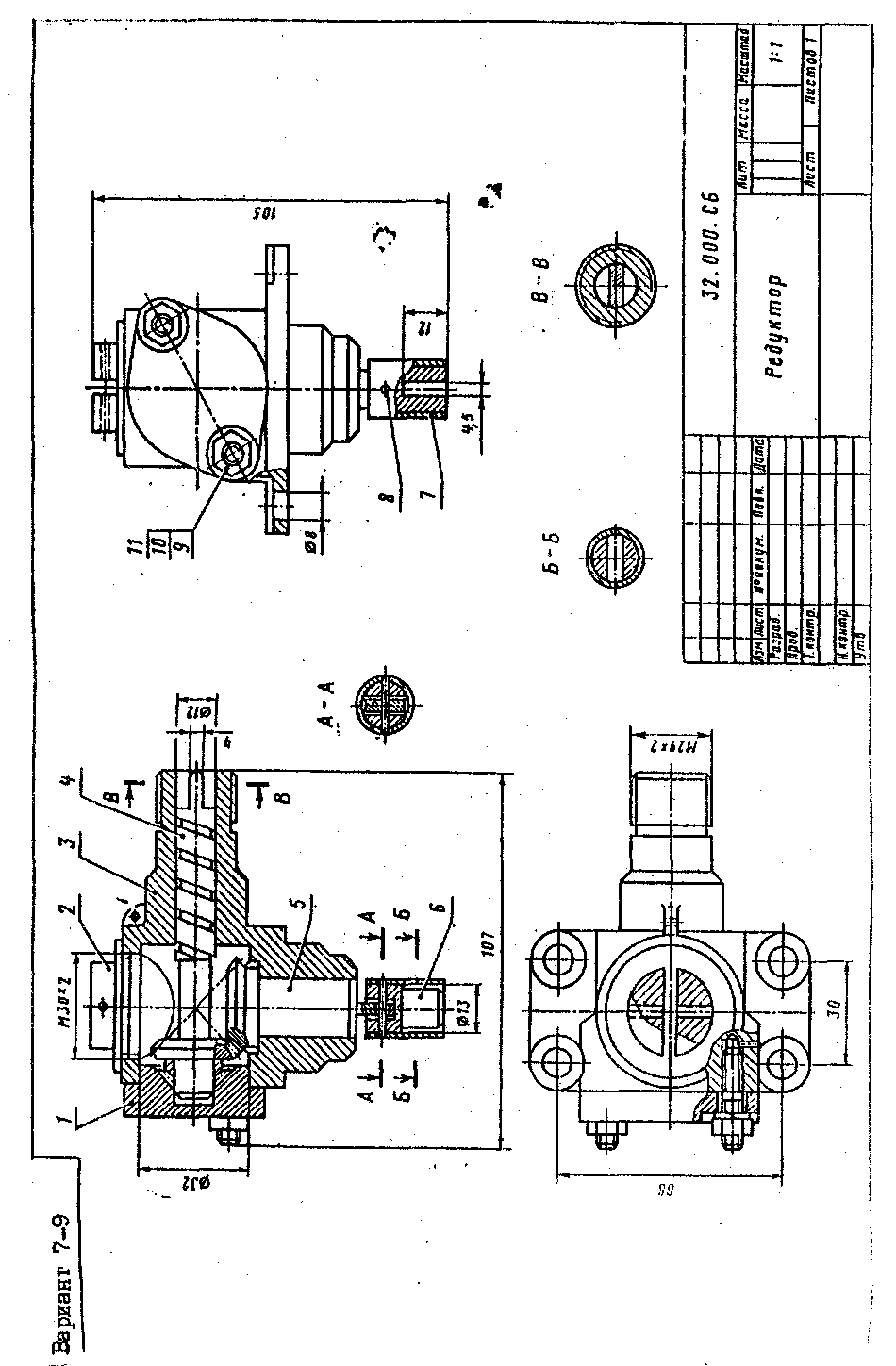
7 8 9	Редуктор конический
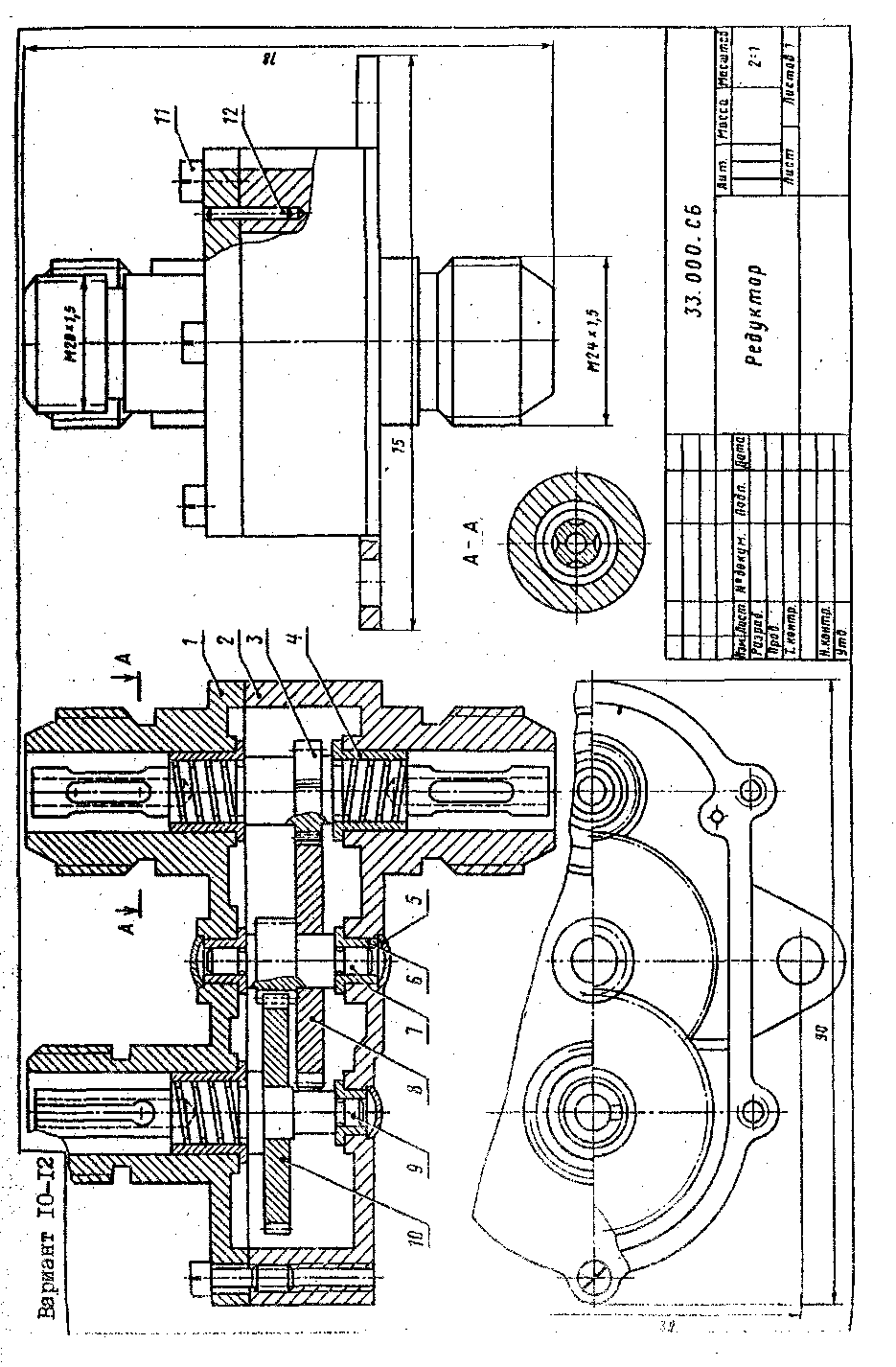
10 11 12	Редуктор цилиндрический
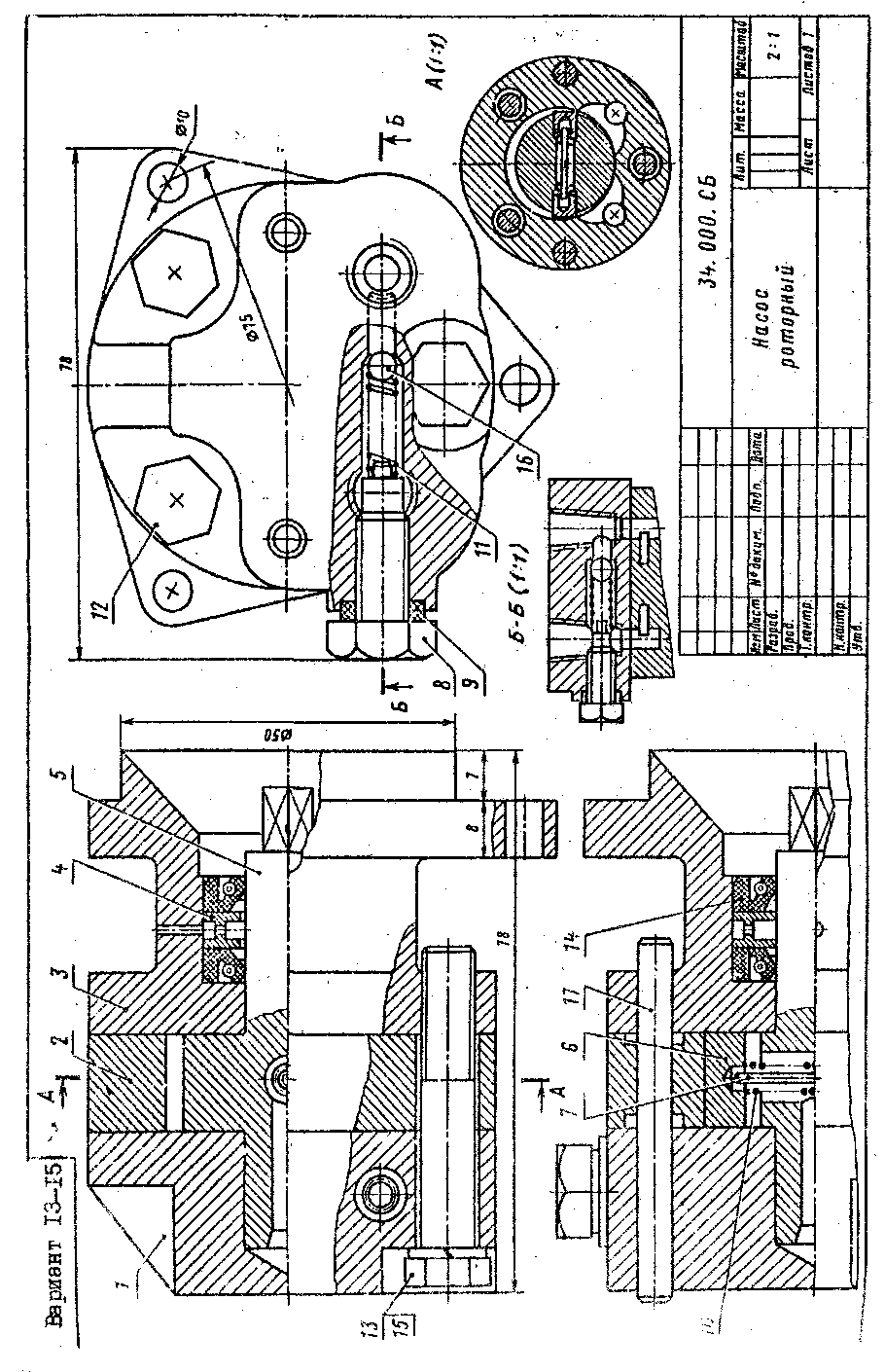
13 14 15	Насос роторный
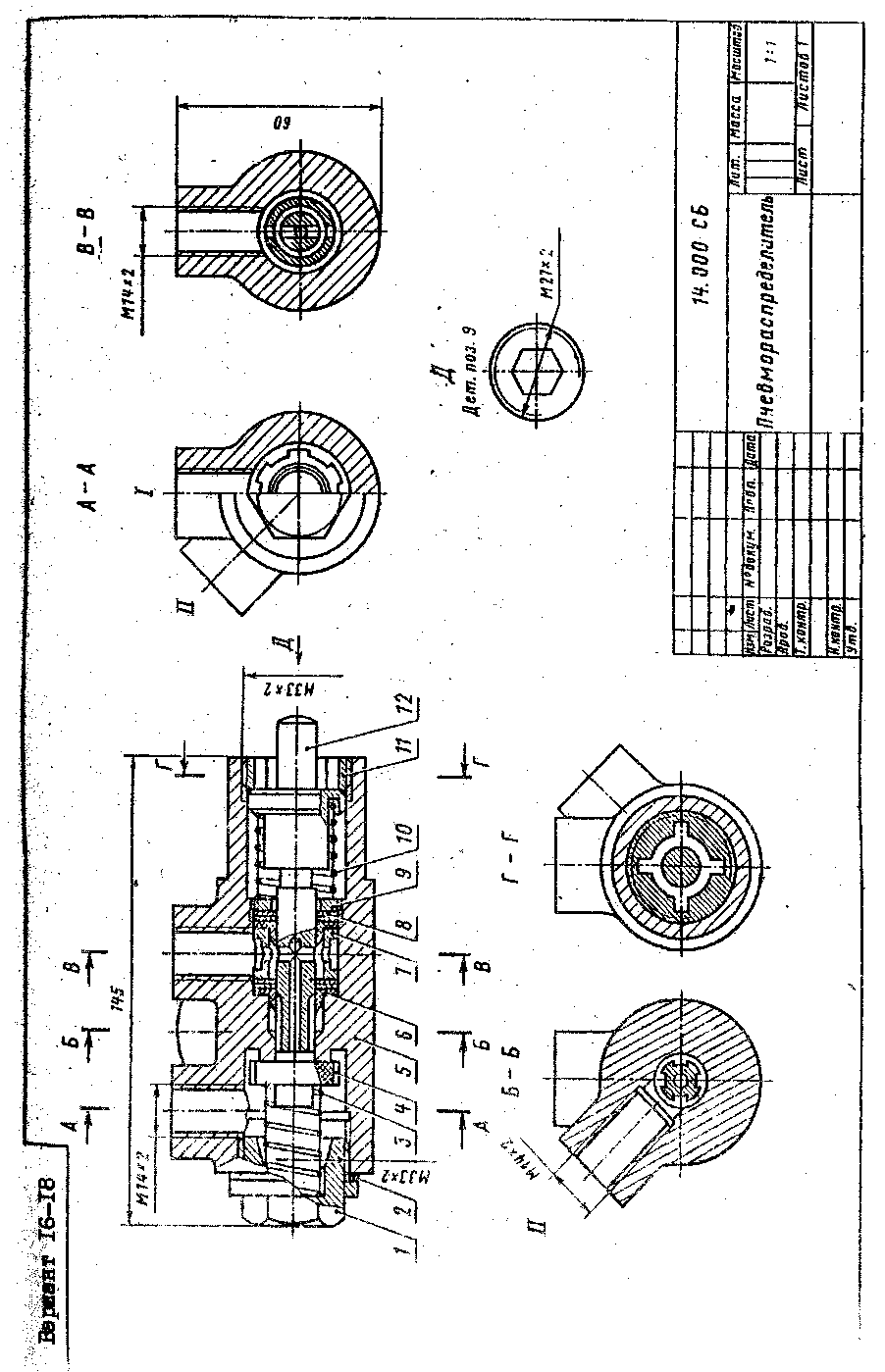
16 17 18	Пневмораспределитель
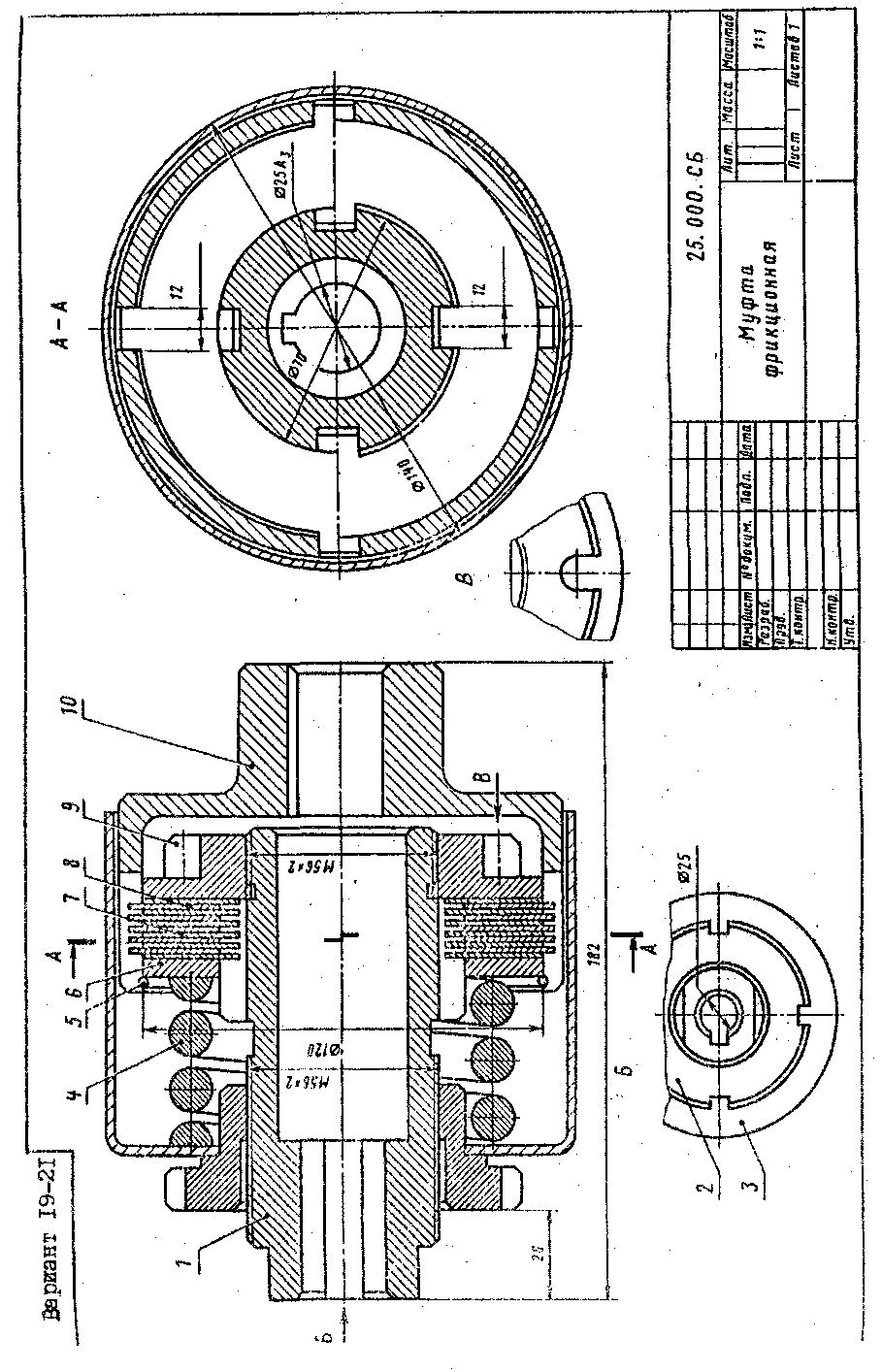
19 20 21	Муфта фрикционная
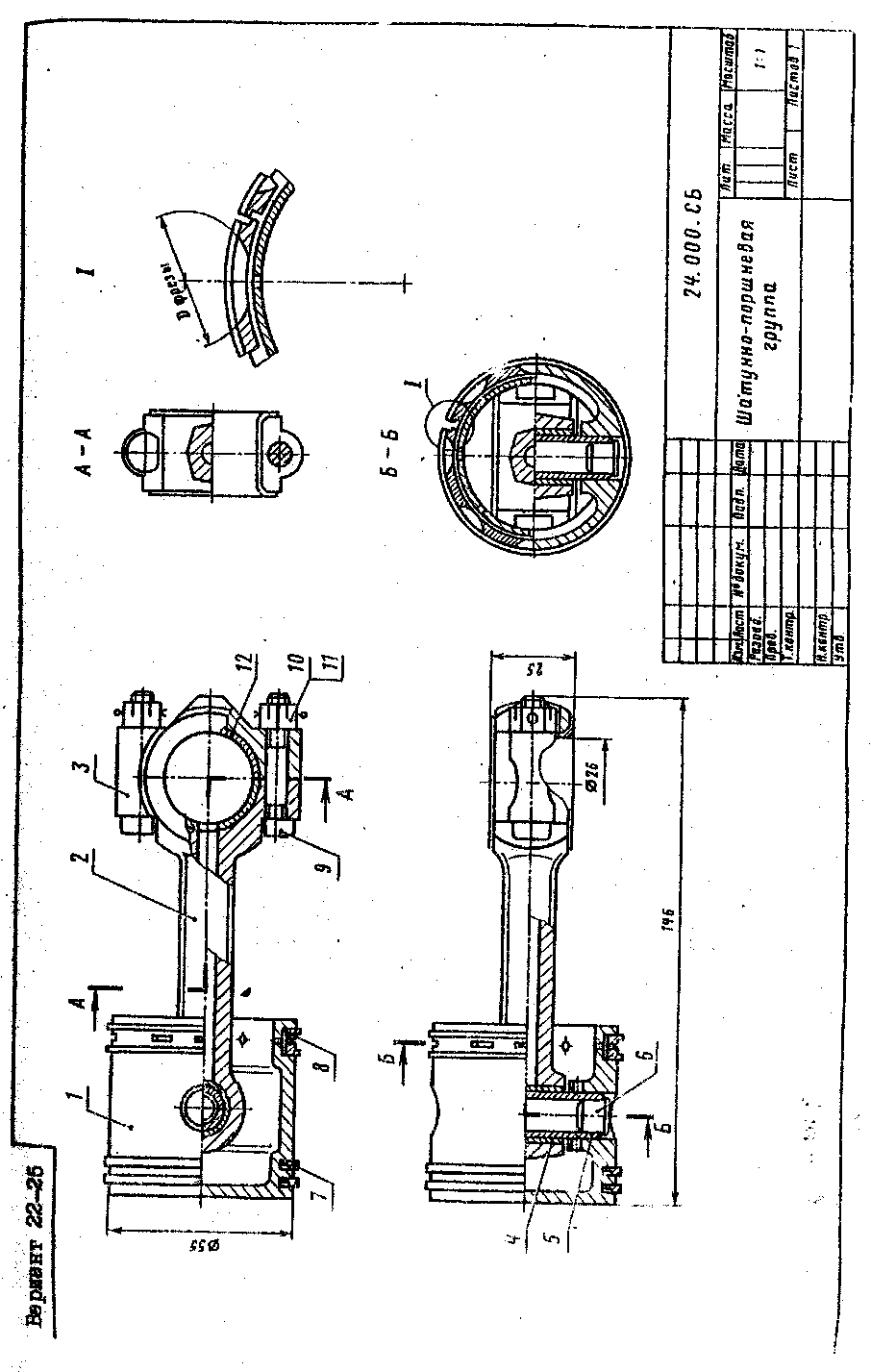
22 23 24 25	Шатунно- поршневая группа

Работа № 5 Уравновешивание кулачкового вала

Цель работы: изучение приемов уравновешивания вращающихся механизмов и решение задачи уравновешивания кулачкового вала.

Краткие теоретические сведения

Неуравновешенностью ротора (вращающегося в опорах тела) называется его состояние, характеризующееся таким распределением мacс, которое за время вращения вызывает переменные нагрузки на морах. Эти нагрузки являются причиной сотрясений и вибраций, преждевременного износа; снижают КПД и производительность машин. Особо нежелательна неуравновешенность в быстроходных машинax. Уравновешивание вращающихся масс механизмов, с тем чтобы уничтожить влияние сил инерции называется балансировкой [12].

Рассмотрим случай статистической неуравновешенности, когда центр тяжести тела не лежит на оси вращения.

Представим себе маховик массой т, вращающийся с постоянной угловой скоростью w. Допустим, что центр тяжести С маховика не нежит на оси вращения, а смещен на величину е_ст называемую эксцентриситетом массы (рис.5.1)

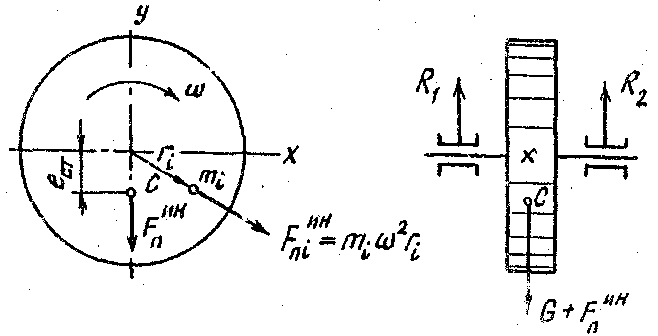
Рис.5.1 Расчетная схема маховика

Силу тяжести маховика обозначим G, массой оси пренебрегаем. Разобьем маховик на ряд материальных точек с массами m_i и определим равнодействующую центробежных сил инерции F^ин_ni. Проекция этой равнодействующей на ось х в следствии симметрии маховика относительно оси у равна нулю, т.е.

;

;

Согласно принципу Даламбера составим уравнение равновесия:

; .

Так как сила инерции F^ин_n во время вращения меняет свое положение, то максимальная сила давления на подшипники будет при нижнем положении центра тяжести:

;

Определим силу давления F_тах на подшипники, если масса маховика т=102 кг, его частота вращения 3000 мин^-1, а эксцентриситет массы е_ст=1 мм.

При

Н;

Н;

Как видно из примера, динамические нагрузки могут во много раз превосходить силу тяжести движущихся частей машины.

Из сказанного выше можно сделать вывод: для уравновешивания вращающегося тела необходимо, чтобы центр тяжести его лежал на оси вращения.

Статистическую неуравновешенность легко обнаружить путем статической балансировки на двух горизонтальных параллельных балансировочных ножах. Деталь, не имеющая статической неуравновешенности, будет находиться на ножах в состояний безразличного равновесия.

Неуравновешенность ротора характеризуется величиной дисбаланса. Произведение неуравновешенной массы на ее эксцентриситет называется значением дисбаланса и выражается в г·мм.

Сформулированное выше условие уравновешивания вращающегося тела не является достаточным, так как динамические нагрузки могут возникнуть и в том случав, когда центр тяжести лежит на оси вращения. Рассмотрим коленчатый вал двухцилиндрового двигателя (рис.5.2).

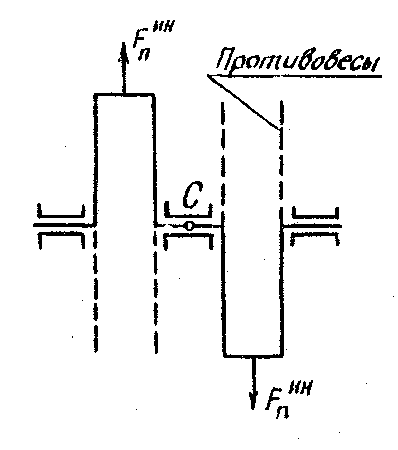
Рисунок 5.2 Схема коленчатого вала

В том случае, даже если центр тяжести С лежит на оси вращения, возникает пара сил инерции F^ин_n, вызывающая изгиб вала и добавочные давления на опоры, меняющиеся по направлению. Такая неуравновешенность называется моментной, и ее можно обнаружить при достаточно быстром вращении, но не в покое. Если статическая и моментная неуравновешенности существуют одновременно, то такая неуравновешенность называется динамической. Причинами неуравновешенности могут быть неточности в изготовлении и сборке деталей, неравномерность распределения материала, деформация деталей, большие зазоры во вращательных парах и т.д. Устраняют неуравновешенность, удаляя (например, высверливая) избыток материала в более тяжелой части детали или добавляя корректирующую массу в более легкой его части. При значительной неуравновешенности ставят противовесы, масса которых иногда достигает десятков тысяч килограммов. В машиностроении статическая и динамическая балансировка производится на балансировочных станках.

Уравновешивание кулачкового вала

Для полного уравновешивания вращающегося в опорах кулачкового вала необходимо, чтобы главный вектор сил инерции Рn и главный момент сил инерции Мn были равны нулю [8]:

;

(5.1)

;

(5.2)

где ω - угловая скорость вращения,

m_i- элементарная масса,

r_i -расстояние элементарной массы от оси вращения,

l_i -расстояние от элементарной массы до плоскости исправления.

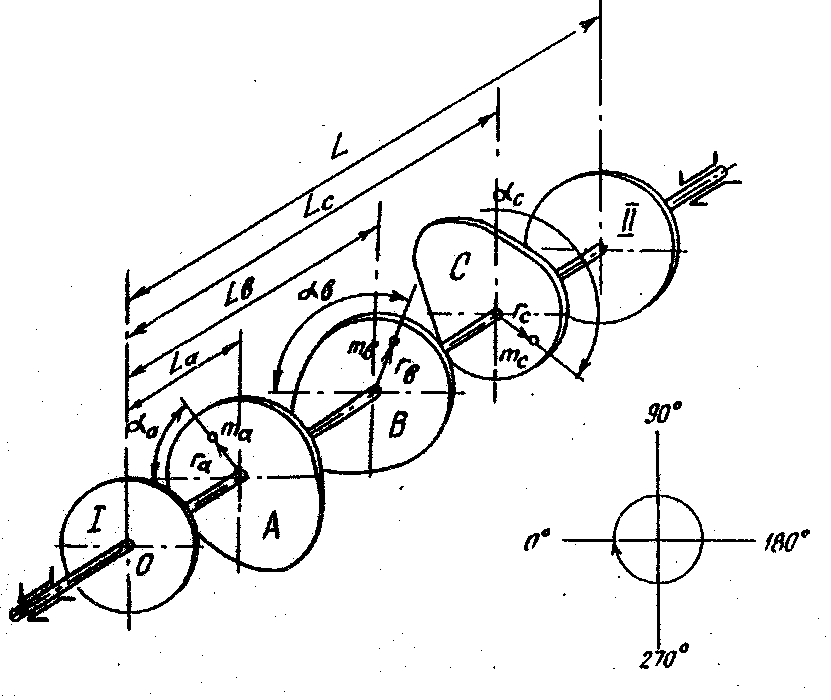
Рис.5.3.Кулачковый вал с корректирующими дисками:

Так как , то для полного уравновешивания необходимо:

;

(5.3)

;

(5.4)

Формула (5.3) выражает условие статической уравновешенности кулачкового вала, а формула (5.4) устанавливает условие его динамической уравновешенности.

Рассмотрим решение поставленной задачи. Пусть, на трех промежуточных кулачках А, В, и С неуравновешенные массы соответственно составляют m_А, m_В и m_C (рис.5.3). Положения неуравновешенных масс на кулачках заданы радиусами-векторами r_A, r_B и r_C с углами отчета α_A, α_B, α_C. Покажем, что с помощью двух масс, расположенных в произвольно выбранных плоскостях исправления, можно осуществить не только статическое, но и динамическое, т.е. полное уравновешивание.

Обозначим крайние диски, на которых будут устанавливаться противовесы, соответственно I и II и будем считать, что плоскости исправления проходят через середины этих дисков. Расстояние между дисками обозначим через L, а расстояния от кулачков А, В, и С до плоскости исправления I -L_А, L_B и L_С. Обозначим вес противовеса при статическом уравновешивании G_n, а радиус-вектор, определяющий положение его центра тяжести - через r_n. Тогда из формулы (5.3), заменяя массы весами будем иметь:

;

(5.5)

Если по уравнению (5.5) построим векторный многоугольник (рис.5.4), то его замыкающий отрезок - вектор определит статический момент уравновешивающей массы:

;

(5.6)

где - масштаб плана, Н*м/мм

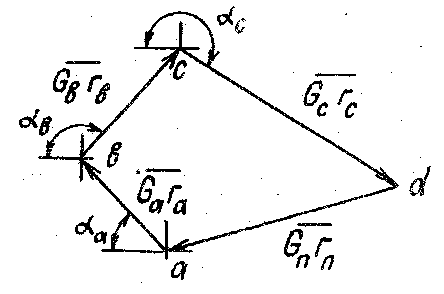
Рисунок 5.4.План статических моментов сил инерции

Задавшись величиной G_n, определим радиус-вектор r_n, соблюдая условие r_n<R_I:

;

(5.7)

Если закрепить противовес G_n на найденном радиусе-векторе r_n в плоскости I, то получим статически уравновешенный кулачковый вал.

Для полного уравновешивания кулачкового вала веса противовесов, устанавливаемых на дисках I и II, обозначим G_I и G_II, а радиусы-векторы, определяющие положение их центров тяжести через r_I и r_II.

Определим сначала центробежные моменты каждой массы относительно точки 0 по формуле (5.4) и сложим их геометрически.

;

(5.8)

По замыкающему отрезку - вектору d_А плана центробежных моментов (рис. 5.5а) находим центробежный момент силы инерции искомого противовеса 6ц> уравновешивающего систему динамически:

;

(5.9)

где - масштаб плана центробежных моментов сил инерции, Н-м2/мм

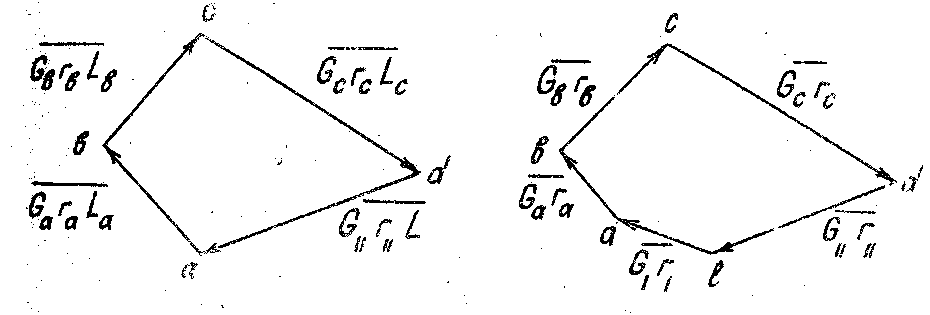
а) б)

Рисунок 5.5 Векторные многоугольники: а) план центробежных моментов сил инерции; б) план статических моментов сил инерции

Затем, выбрав радиус-вектор r_II из условия r_II<R_II, при известном расстоянии между плоскостями исправления L, находим статический момент

;

(5.10)

и вес противовеса:

;

(5.11)

Если противовес G_II установить на диске в плоскости направления II, получим динамически уравновешенную систему. Для ее статического уравновешивания построим второй многоугольник по формуле (5.3) - план статических моментов (рис. 5.5б). Его замыкающий отрезок - вектор определяет статический момент уравновешивающего груза:

;

(5.12)

где - масштаб плана, Н*м/мм.

Если закрепить противовес на диске в плоскости исправления I, то получим (т.к. L_I=0) и план центробежных моментов инерции (рис.5.5а) по-прежнему останется замкнутым, т.е. динамическая уравновешенность не нарушится.

В результате раздельного статического и динамического уравновешивания в плоскости поправления I оказался противовес G_I, а в плоскости II противовес G_II. Эти противовесы, в общем случае не равны, расположены в разных диаметральных плоскостях, а развиваемые ими центробежные силы перекрещиваются.