|
Билет
1.
Понятие
вектора. Линейные операции над
векторами. Их свойства.
Векторы.
Основные понятия
Вектором называется
направленный отрезок. Обозначается
вектор  , , 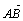 , ,  , ,  , AB, a (А –
начало вектора, В –
его конец). , AB, a (А –
начало вектора, В –
его конец).
Нулевым
вектором (обозначается  )
называется вектор, начало и конец
которого совпадают. )
называется вектор, начало и конец
которого совпадают.
Расстояние
между началом и концом вектора
называется его длиной,
или модулем,
или абсолютной
величиной (обозначается  , ,  ). ).
Векторы
называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых (обозначают  ,
а также ,
а также  ,
если векторы сонаправлены, и ,
если векторы сонаправлены, и  ,
если они противоположно направлены). ,
если они противоположно направлены).
Векторы
называются компланарными,
если они лежат в одной плоскости или
в параллельных плоскостях.
Два
вектора называются равными,
если они сонаправлены ( )
и имеют равные длины ( )
и имеют равные длины ( ).
Обозначают ).
Обозначают  . .
Для
каждого вектора  ,
отличного от нулевого вектора,
существует противоположный вектор,
который обозначается ,
отличного от нулевого вектора,
существует противоположный вектор,
который обозначается  и
удовлетворяет условиям: и
удовлетворяет условиям:  , ,  . .
Вектором называется
направленный отрезок. Обозначается
вектор  , ,  , ,  , ,  , AB, a (А –
начало вектора, В –
его конец). , AB, a (А –
начало вектора, В –
его конец).
Нулевым
вектором (обозначается  )
называется вектор, начало и конец
которого совпадают. )
называется вектор, начало и конец
которого совпадают.
Расстояние
между началом и концом вектора
называется его длиной,
или модулем,
или абсолютной
величиной (обозначается  , ,  ). ).
Векторы
называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых (обозначают  ,
а также ,
а также  ,
если векторы сонаправлены, и ,
если векторы сонаправлены, и  ,
если они противоположно направлены). ,
если они противоположно направлены).
Векторы
называются компланарными,
если они лежат в одной плоскости или
в параллельных плоскостях.
Два
вектора называются равными,
если они сонаправлены ( )
и имеют равные длины ( )
и имеют равные длины ( ).
Обозначают ).
Обозначают  . .
Для
каждого вектора  ,
отличного от нулевого вектора,
существует противоположный вектор,
который обозначается ,
отличного от нулевого вектора,
существует противоположный вектор,
который обозначается  и
удовлетворяет условиям: и
удовлетворяет условиям:  , ,  . .
|
Линейные
операции над векторами
|
|
Линейными
операциями называют
операции сложения и вычитания
векторов и умножения вектора на
число.
Сложение
векторов. Пусть 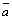 и и  –
два произвольных вектора. Возьмем
произвольную точку О и
построим вектор –
два произвольных вектора. Возьмем
произвольную точку О и
построим вектор  ;
затем от точки А отложим
вектор ;
затем от точки А отложим
вектор  .
Вектор .
Вектор  ,
соединяющий начало первого слагаемого
вектора с концом второго,
называется суммой этих
векторов и обозначается ,
соединяющий начало первого слагаемого
вектора с концом второго,
называется суммой этих
векторов и обозначается 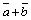 (рис.
1). (рис.
1).
 Рис.
1 Рис.
1
Ту
же сумму можно получить иным способом.
Отложим от точки О векторы  и и  .
Построим на этих векторах как на
сторонах параллелограмм ОАСВ.
Вектор .
Построим на этих векторах как на
сторонах параллелограмм ОАСВ.
Вектор  –
диагональ параллелограмма – является
суммой векторов –
диагональ параллелограмма – является
суммой векторов  и и  (рис.
2). (рис.
2).
 Рис.
2 Рис.
2
Понятие
суммы можно обобщить на случай любого
конечного числа слагаемых (рис. 3).
 Рис.
3 Рис.
3
Вычитание
векторов. Разностью  векторов векторов  и и  называется
такой вектор называется
такой вектор  ,
который в сумме с вектором ,
который в сумме с вектором  дает
вектор дает
вектор  : :   . .
Если
векторы  и и  привести
к общему началу, то разность
представляет собой отрезок, соединяющий
их концы и направленный от «вычитаемого»
к «уменьшаемому» (рис. 4). привести
к общему началу, то разность
представляет собой отрезок, соединяющий
их концы и направленный от «вычитаемого»
к «уменьшаемому» (рис. 4).

Рис.
4
Таким
образом, если на векторах  и и  ,
отложенных из общей точки О,
построить параллелограмм ОАСВ,
то вектор ,
отложенных из общей точки О,
построить параллелограмм ОАСВ,
то вектор  ,
совпадающий с одной диагональю,
равен сумме ,
совпадающий с одной диагональю,
равен сумме  ,
а вектор ,
а вектор  ,
совпадающий с другой диагональю, –
разности ,
совпадающий с другой диагональю, –
разности  (рис.
5). (рис.
5).
 Рис.
5 Рис.
5
Умножение
вектора на число. Произведением вектора  на
действительное число на
действительное число  называется
вектор называется
вектор  (обозначают (обозначают  ),
определяемый следующими условиями: ),
определяемый следующими условиями:
1)  , ,
2)  при при  и и  при при  . .
Очевидно,
что при   . .
Построим,
например, векторы  и и  для
заданного вектора для
заданного вектора  (рис.
6). (рис.
6). Рис.
6 Рис.
6
Из
определения следует: два
вектора  и и  коллинеарны
тогда и только тогда, когда имеет
место равенство коллинеарны
тогда и только тогда, когда имеет
место равенство  : :
 (2.1) (2.1)
Свойства
линейных операций:
1)  ; ;
2)  ; ;
3)  ; ;  ; ;
4)  ; ;
5)  ; ;
6)  ; ;
7)  ; ;  ; ;
Пусть
дан вектор  . Ортом вектора . Ортом вектора  (обозначается (обозначается  )
называется вектор единичной длины,
сонаправленный с вектором )
называется вектор единичной длины,
сонаправленный с вектором  . .
Очевидно,  для
любого вектора для
любого вектора  . .
|
|
Билет
3.
Базис
в плоскости и пространстве. Разложение
по базису. Линейные свойства координат
вектора.
Рассмотрим
декартову прямоугольную систему
координат Oxyz.
Обозначим  , ,  , ,  –
единичные
векторы, направленные
соответственно вдоль осей Ox, Oy, Oz (орты
осей). Эти векторы называются декартовым
прямоугольным базисом в
пространстве. –
единичные
векторы, направленные
соответственно вдоль осей Ox, Oy, Oz (орты
осей). Эти векторы называются декартовым
прямоугольным базисом в
пространстве.
Пусть  –
произвольный вектор в пространстве.
Перенесем его начало в точку O ( –
произвольный вектор в пространстве.
Перенесем его начало в точку O ( )
и построим прямоугольный параллелепипед,
в котором вектор )
и построим прямоугольный параллелепипед,
в котором вектор  является
диагональю (рис. 11). Тогда является
диагональю (рис. 11). Тогда  ,
где ,
где  , ,  , ,  –
составляющие вектора –
составляющие вектора  по
осям Ox, Oy, Oz.
Но по
осям Ox, Oy, Oz.
Но  ,
аналогично ,
аналогично , ,
 . .
 Рис.
11 Рис.
11
Обозначая  , ,  , ,  ,
получим ,
получим  . .
Это
равенство называется разложением
вектора  по
базису по
базису  , ,  , ,  , а
числа , а
числа  , ,  , ,  называются координатами вектора называются координатами вектора  в
этом базисе,
или декартовыми прямоугольными
координатами вектора. Пишут в
этом базисе,
или декартовыми прямоугольными
координатами вектора. Пишут  или или  . .
Таким
образом, прямоугольные декартовы
координаты вектора – это его проекции
на соответствующие оси координат.
Зная
координаты вектора, легко выразить
его длину:
 (2.2) (2.2)
(квадрат
диагонали прямоугольного параллелепипеда
равен сумме квадратов его измерений).
Если  ,
где ,
где  , ,  ,
то ,
то  , ,  , ,  .
Тогда .
Тогда  ,
или ,
или

так
выражаются координаты вектора через
координаты его начала и конца.
Из
свойств проекций (а координаты вектора
– это его проекции на оси координат)
следует:
если  , ,  , ,  ,
то ,
то
1)  , ,  , ,  –
равные векторы имеют соответственно
равные координаты; –
равные векторы имеют соответственно
равные координаты;
2)  –
при сложении векторов их координаты
складываются, при вычитании –
вычитаются; –
при сложении векторов их координаты
складываются, при вычитании –
вычитаются;
3)  –
при умножении вектора на число его
координаты умножаются на это число; –
при умножении вектора на число его
координаты умножаются на это число;
4)  , ,  , ,  ,
то есть ,
то есть  – –
координаты
коллинеарных векторов пропорциональны.
Билет
5.
Скалярное
произведение, его свойства. Выражение
через координаты сомножителей.
|
Скалярное
произведение векторов
|
|
Скалярным
произведением двух
векторов (обозначается  или или  )
называется число, равное произведению
длин этих векторов на косинус угла
между ними: )
называется число, равное произведению
длин этих векторов на косинус угла
между ними:  ,
где ,
где  . .
Учитывая,
что  , ,  ,
можно записать: ,
можно записать:  .
Отсюда .
Отсюда
 . (2.8) . (2.8)
Из
физики известно: если  –
постоянная сила, действующая на
материальную точку, а –
постоянная сила, действующая на
материальную точку, а  –
вектор перемещения точки под действием
этой силы, то работа, совершаемая
силой –
вектор перемещения точки под действием
этой силы, то работа, совершаемая
силой  на
участке l,
равна на
участке l,
равна  . .
Свойства
скалярного произведения:
1)  ; ;
2)  ; ;
3)  ; ;
4)  ,
или ,
или  ,
или . ,
или .

Таким
образом,  –
условие перпендикулярности векторов. –
условие перпендикулярности векторов.
5)  ,
или, обозначая ,
или, обозначая  (скалярный
квадрат вектора (скалярный
квадрат вектора  ),
получим ),
получим  ,
откуда ,
откуда  . .
Пусть
известны координаты векторов  и и  : :  , ,  . .
Тогда  

Таким
образом,

|
|
Билет
4.
Ортонормированные
базисы. Их свойства. Проекция вектора
на ось. Направляющий косинус вектора.
Ортогональный
(ортонормированный)
базис — ортогональная (ортонормированная)
система элементов линейного
пространства со скалярным
произведением,
обладающая свойством полноты.
Конечномерный
случай
Ортогональный
базис — базис,
составленный из попарно ортогональных векторов.
Ортонормированный
базис удовлетворяет
еще и условию единичности нормы всех
его элементов. То есть это ортогональный
базис с нормированными элементами.
Последнее
удобно записывается при помощи символа
Кронекера:

то
есть скалярное
произведение каждой
пары базисных векторов равно нулю,
когда они не совпадают ( ),
и равно единице при совпадающем
индексе, то есть когда берется скалярное
произведение любого базисного вектора
с самим собой. ),
и равно единице при совпадающем
индексе, то есть когда берется скалярное
произведение любого базисного вектора
с самим собой.
Очень
многое записывается в ортогональном
базисе гораздо проще, чем в произвольном,
поэтому очень часто стараются
использовать именно такие базисы,
если только это возможно или использование
какого-то специального неортогонального
базиса не дает особых специальных
удобств. Или если не отказываются от
него в пользу базиса общего вида из
соображений общности.
Ортонормированный
базис является самодуальным (дуальный ему
базис совпадает с ним самим). Поэтому
в нём можно не делать различия между
верхними и нижними индексами, и
пользоваться, скажем, только нижними
(как обычно и принято, если конечно
при этом используются только
ортонормированные базисы).
Линейная
независимость следует из ортогональности,
то есть достигается для ортогональной
системы векторов автоматически.
Коэффициенты
в разложении вектора по ортогональному
базису:

можно
найти так:
 . .
Полнота
ортонормированной системы векторов
эквивалентна равенству
Парсеваля:
для любого вектора  квадрат
нормы вектора равен сумме квадратов
коэффициентов его разложения по
базису: квадрат
нормы вектора равен сумме квадратов
коэффициентов его разложения по
базису:

Аналогичные
соотношения имеют место и для
бесконечномерного случая (см. ниже).
Бесконечномерный
случай
Ортогональный
базис —
система попарно ортогональных
элементов e1,e2,...,en,... гильбертова
пространства X такая,
что любой элемент  однозначно
представим в виде сходящегося по норме
ряда однозначно
представим в виде сходящегося по норме
ряда
 называемого рядом
Фурье элемента x по
системе {en}.
называемого рядом
Фурье элемента x по
системе {en}.
Часто
базис {en} выбирается
так, что | en |
= 1,
и тогда он называется ортонормированным
базисом.
В этом случае числа an,
называются коэффициентами Фурье
элемента x по
ортонормированному базису {en},
имеют вид
an =
(x,en).
Необходимым
и достаточным условием того, чтобы
ортонормированная система {en} была
базисом, является равенство
Парсеваля.
Гильбертово
пространство, имеющее ортонормированный
базис, является сепарабельным,
и обратно, во всяком сепарабельном
гильбертовом пространстве существует
ортонормированный базис.
Если
задана произвольная система
чисел {an} такая,
что  ,
то в случае гильбертова пространства
с ортонормированным базисом {en} ряд ,
то в случае гильбертова пространства
с ортонормированным базисом {en} ряд  —
сходится по норме к некоторому
элементу —
сходится по норме к некоторому
элементу 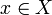 .
Этим устанавливается изоморфизм
любого сепарабельного гильбертова
пространства пространству l2 (теорема
Рисса —
Фишера). .
Этим устанавливается изоморфизм
любого сепарабельного гильбертова
пространства пространству l2 (теорема
Рисса —
Фишера).
Примеры
Стандартный
базис в
n-мерном евклидовом пространстве Rn является
ортонормированным. в
n-мерном евклидовом пространстве Rn является
ортонормированным.
Множество  образует
ортонормированый базис в L2([-π,
π] образует
ортонормированый базис в L2([-π,
π]
|
Проекция
вектора на ось
|
|
Углом
между двумя ненулевыми
векторами  и и  называется
наименьший угол называется
наименьший угол  ( ( ),
на который надо повернуть один из
векторов до его совпадения со вторым.
Предварительно
нужно привести векторы к общему
началу О (рис.
7). ),
на который надо повернуть один из
векторов до его совпадения со вторым.
Предварительно
нужно привести векторы к общему
началу О (рис.
7).
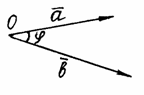 Рис.
7 Рис.
7
Под углом
между вектором  и
осью и
осью  понимают
угол между векторами понимают
угол между векторами  и и  (рис.
8). (рис.
8).
 Рис.
8 Рис.
8
Пусть  –
некоторая ось, а –
некоторая ось, а  –
вектор, произвольно расположенный
в пространстве. Обозначим –
вектор, произвольно расположенный
в пространстве. Обозначим  и и  –
проекции на ось –
проекции на ось  соответственно
начала А и
конца В этого
вектора (рис. 9). Вектор соответственно
начала А и
конца В этого
вектора (рис. 9). Вектор  называется
составляющей вектора называется
составляющей вектора  по
оси по
оси  . .

Рис.
9
Проекцией вектора  на
ось на
ось  (обозначается пр (обозначается пр )
называется длина его составляющей )
называется длина его составляющей  по
этой оси, взятая со знаком «плюс»,
если по
этой оси, взятая со знаком «плюс»,
если  ,
и со знаком «минус», если ,
и со знаком «минус», если  . .
Очевидно,
что пр ,
если вектор ,
если вектор  образует
острый угол с осью образует
острый угол с осью 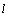 ; пр ; пр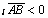 ,
если этот угол тупой; пр ,
если этот угол тупой; пр ,
если ,
если  . .
Если
известны координаты точек  и и  на
оси: на
оси:  , ,  ,
то пр ,
то пр . .
Нетрудно
доказать свойства
проекций:
1) Равные
векторы имеют равные проекции на
одну и ту же ось.
2) пр пр пр пр пр . .
3) пр пр пр , ,  . .
4) пр ,
где ,
где 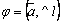 –
угол между вектором и осью. –
угол между вектором и осью.
Заметим,
что проекция вектора на ось и его
составляющая связаны соотношением сост пр пр . .
|
|
Направляющие
косинусы вектора
|
|
Направление
вектора в пространстве определяется
углами  ,
которые вектор образует с осями
координат (рис. 12). Косинусы этих
углов называются направляющими
косинусами вектора: ,
которые вектор образует с осями
координат (рис. 12). Косинусы этих
углов называются направляющими
косинусами вектора:  , ,  , , 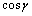 . .

Рис.
12
Из
свойств проекций: , ,  , ,  .
Следовательно, .
Следовательно,
 , ,  , ,  . (2.5) . (2.5)
Легко
показать, что
1)  ; ;
2) координаты
любого единичного вектора совпадают
с его направляющими косинусами:  . .
|
|


 Рис.
3
Рис.
3 Рис.
5
Рис.
5 Рис.
11
Рис.
11
