|
Билет
6.
Векторное
произведение, его свойства. Выражение
через кординаты сомножителей.
|
Векторное
произведение векторов
|
|
Упорядоченная
тройка некомпланарных векторов
называется правой,
если из конца третьего вектора
кратчайший поворот от первого ко
второму виден против часовой стрелки.
В противном случае тройка
называется левой (начала
векторов тройки предполагаются
совмещенными).
Так,
на рис. 16 тройка  , ,  , ,  –
правая, а тройка –
правая, а тройка  , , , ,
 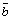 –
левая (из конца вектора –
левая (из конца вектора 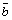 кратчайший
поворот от кратчайший
поворот от  к к  виден
по часовой стрелке). виден
по часовой стрелке). Рис.
16 Рис.
16
Векторным
произведением двух
векторов называется вектор, который
обозначается  или или  и
определяется следующим образом: и
определяется следующим образом: 
1)  где где  –
длина этого вектора равна произведению
длин перемножаемых векторов на синус
угла между ними; –
длина этого вектора равна произведению
длин перемножаемых векторов на синус
угла между ними;
2)  , , –
этот вектор перпендикулярен каждому
из перемножаемых векторов; –
этот вектор перпендикулярен каждому
из перемножаемых векторов;
3) векторы  , , 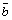 , ,  образуют
правую тройку. образуют
правую тройку.
Из
условия (1) следует, что модуль
вектора численно
равен площади параллелограмма,
построенного на векторах численно
равен площади параллелограмма,
построенного на векторах  и и  как
на сторонах (рис 17): как
на сторонах (рис 17):  , ,  . .
 Рис.
17 Рис.
17
Из
физики известно: если  –
сила, приложенная к точке М,
то момент –
сила, приложенная к точке М,
то момент  этой
силы относительно точки А равен
векторному произведению
векторов этой
силы относительно точки А равен
векторному произведению
векторов  и и  : :  . .
Свойства
векторного произведения:
1)  ; ;
2)  ; ;
3)  ; ;
4)  ,
или ,
или  ,
или ,
или  ; ;
4a)  . .
Заметим,
что из определения и свойств следует: 
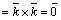 ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  . .
Пусть
известны координаты векторов  и и  : :  , ,  .
Тогда .
Тогда 
=[по
свойствам 2, 3]
 [на
основании замечания] [на
основании замечания]
 . .
Таким
образом,
 . .
|
Билет
9.
Прямая
на плоскости. Различные формы уравнения
прямой. Простейшие задачи.
|
Прямая
на плоскости
|
|
Пусть  –
заданная точка на прямой –
заданная точка на прямой  , ,  –
вектор, перпендикулярный прямой –
вектор, перпендикулярный прямой  ,
его называют нормальным
вектором прямой,
и пусть ,
его называют нормальным
вектором прямой,
и пусть  –
произвольная точка прямой –
произвольная точка прямой  (рис.
20). Тогда (рис.
20). Тогда  , ,  ,
то есть ,
то есть
 . (2.12) . (2.12)
(2.12)
– уравнение прямой, проходящей через
данную точку перпендикулярно данному
вектору.
 Рис.
20 Рис.
20
Раскрыв
скобки и сгруппировав слагаемые в
(2.12), получим  .
Обозначим .
Обозначим  ,
уравнение примет вид ,
уравнение примет вид
 . (2.13) . (2.13)
(2.13)
– общее уравнение прямой на плоскости.
Если
в уравнении (2.13) , ,  , ,  ,
то, перенеся слагаемое С в
правую часть и разделив на него обе
части уравнения, получим ,
то, перенеся слагаемое С в
правую часть и разделив на него обе
части уравнения, получим
 ,
или ,
или  .
Обозначим .
Обозначим  , ,  ,
тогда уравнение примет вид ,
тогда уравнение примет вид
 (2.14) (2.14)
(2.14)
– уравнение прямой в отрезках,
здесь a и b –
отрезки, отсекаемые прямой на осях
координат (рис. 21): из уравнения (2.13)
при  получим получим  ,
а при ,
а при   . .
 Рис.
21 Рис.
21
Пусть  –
заданная точка на прямой –
заданная точка на прямой 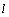 , ,  –
вектор, параллельный прямой, его
называют направляющим
вектором прямой,
и пусть –
вектор, параллельный прямой, его
называют направляющим
вектором прямой,
и пусть  –
произвольная точка прямой –
произвольная точка прямой  (рис.
22). Тогда (рис.
22). Тогда
 , ,  
. (2.15)
(2.15)
– каноническое
уравнение прямой,
или уравнение прямой, проходящей
через данную точку параллельно
данному вектору.
 Рис.
22 Рис.
22
В
частности, если прямая  параллельна
оси параллельна
оси  ,
то ее направляющий вектор ,
то ее направляющий вектор  ,
и каноническое уравнение имеет
вид ,
и каноническое уравнение имеет
вид  ,
или ,
или .
Если .
Если  ,
то ,
то  ,
и каноническое уравнение прямой ,
и каноническое уравнение прямой  ,
или ,
или  . .
Если
в уравнении (2.15) величину отношения
положить равной  (
( –
параметр, переменная величина, –
параметр, переменная величина,  ): ):
 , ,  ,
то, выразив ,
то, выразив  и и  из
уравнений, получим из
уравнений, получим
 , ,  . (2.16) . (2.16)
(2.16) –
параметрические
уравнения прямой.
Пусть
на прямой  заданы
две точки заданы
две точки  и и  .
Тогда вектор .
Тогда вектор  является
направляющим вектором прямой и,
используя уравнение (2.15), можно
записать является
направляющим вектором прямой и,
используя уравнение (2.15), можно
записать
 . (2.17) . (2.17)
(2.17)
– уравнение прямой, проходящей через
две данные точки.
Пусть  –
заданная точка на прямой –
заданная точка на прямой  , ,  –
угол наклона прямой к оси –
угол наклона прямой к оси  , ,  (рис.
23). В качестве направляющего вектора
прямой (рис.
23). В качестве направляющего вектора
прямой  возьмем
единичный вектор возьмем
единичный вектор  .
Координаты единичного вектора
совпадают с его направляющими
косинусами, поэтому .
Координаты единичного вектора
совпадают с его направляющими
косинусами, поэтому  , но , но 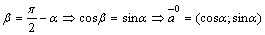 .
Используя уравнение (2.15), получим .
Используя уравнение (2.15), получим  ,
или ,
или  .
Обозначив .
Обозначив  ( ( –
угловой коэффициент прямой), получим
уравнение –
угловой коэффициент прямой), получим
уравнение
 . (2.18) . (2.18)
 Рис.
23 Рис.
23
Выразив
из (2.18)  : :  и
обозначив и
обозначив  ,
получим ,
получим
 . (2.19) . (2.19)
(2.18),
(2.19) – уравнения прямой с угловым
коэффициентом.
В уравнении (2.19)  –
ордината точки пересечения прямой
с осью –
ордината точки пересечения прямой
с осью  . .
Угол
между двумя прямыми. Пусть
прямые  и и  заданы
соответственно уравнениями заданы
соответственно уравнениями  , ,  ,
где ,
где  , ,  .
Обозначим .
Обозначим  угол
между прямыми: угол
между прямыми:  (рис.
24). Тогда (рис.
24). Тогда  , ,  . .
 Рис.
24 Рис.
24
Таким
образом,
 . (2.20) . (2.20)
Если  ,
то ,
то  ,
а следовательно, ,
а следовательно,  ,
то есть k1= k2. ,
то есть k1= k2.
Если  ,
то ,
то  , ,  не
определен, не
определен,  ,
следовательно, ,
следовательно,  ,
или ,
или  . .
Если
прямые  и и  заданы
соответственно уравнениями заданы
соответственно уравнениями
 , ,  ,
где ,
где  , , 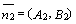 –
нормальные векторы прямых, то –
нормальные векторы прямых, то ,
или ,
или  . .
Если  ,
то ,
то  ,
следовательно, ,
следовательно,  . .
Если  , , 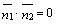 ,
то есть ,
то есть  . .
Расстояние
от точки до прямой. Пусть
прямая  на
плоскости задана уравнением на
плоскости задана уравнением  и
точка и
точка  имеет
координаты имеет
координаты  (рис.
25). (рис.
25).
Обозначим  –
основание перпендикуляра, опущенного
из точки –
основание перпендикуляра, опущенного
из точки  на
прямую на
прямую  , ,  , ,  – расстояние
от точки – расстояние
от точки  до
прямой до
прямой  .
Тогда .
Тогда  ,
а ,
а  – нормальный
вектор прямой. Рассмотрим скалярное
произведение – нормальный
вектор прямой. Рассмотрим скалярное
произведение  . С
одной стороны, . С
одной стороны,  ,
так как ,
так как  ,
следовательно, угол между ними ,
следовательно, угол между ними  или или .
С другой стороны, .
С другой стороны,  ,
но точка ,
но точка  ,
поэтому ее координаты удовлетворяют
уравнению ,
поэтому ее координаты удовлетворяют
уравнению  ,
откуда ,
откуда  ,
поэтому ,
поэтому  .
Приравнивая выражения, получим .
Приравнивая выражения, получим
 .
Тогда .
Тогда  или или
 . (2.21) . (2.21)

Рис.
25
|
|
Билет7.
Смешанное
произведение, его свойства. Выражение
через кординаты сомножителей.
|
|
|
Смешанным,или векторно-скалярным произведением трех_векторов
(обозначается  )
называется произведение вида )
называется произведение вида  . .
Пусть
известны координаты векторов:  , ,  , , .
Векторное произведение векторов .
Векторное произведение векторов и и  –
это вектор с координатами –
это вектор с координатами 
 . .
Скалярное
произведение вектора  на
вектор на
вектор  : : 
Таким
образом,
 . (2.11) . (2.11)
Нетрудно
показать, что  . .
Отложим
данные некомпланарные векторы 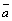 , ,  , ,  от
общего начала и построим на них как
на ребрах параллелепипед (рис. 18). от
общего начала и построим на них как
на ребрах параллелепипед (рис. 18).
 Рис.
18 Рис.
18
По
определению скалярного произведения   ,
где ,
где 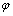 –
угол между векторами –
угол между векторами  и и 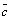 .
Но .
Но  –
площадь параллелограмма, построенного
на векторах –
площадь параллелограмма, построенного
на векторах  и и  ,
а ,
а 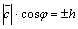 ,
где ,
где 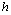 –
высота параллелепипеда. Таким
образом, –
высота параллелепипеда. Таким
образом,  . .
Смешанное
произведение трех векторов с точностью
до знака равно объему параллелепипеда,
построенного на этих векторах как
на ребрах. Можно записать:  . .
Объем
тетраэдра, построенного на
векторах  , ,  , ,  (рис.
19) равен (рис.
19) равен  . .
 Рис.
19 Рис.
19
Заметим,
что если векторы , , 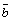 , , 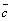 образуют
правую тройку, то образуют
правую тройку, то  и и ,
а если левую, то ,
а если левую, то  и и  . .
Теорема. Для
того чтобы три вектора были компланарны,
необходимо и достаточно, чтобы их
смешанное произведение равнялось
нулю.
Доказательство.
Необходимость. Пусть
векторы  , , 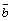 , ,  компланарны.
Можно считать, что они лежат в одной
плоскости. Тогда вектор компланарны.
Можно считать, что они лежат в одной
плоскости. Тогда вектор  перпендикулярен
этой плоскости, следовательно, перпендикулярен
этой плоскости, следовательно,  , ,
а
значит, их скалярное произведение
равно нулю, то есть  . .
Достаточность. Пусть  .
Предположим, что векторы
некомпланарны.
Но тогда существует параллелепипед,
построенный на этих векторах, объем
которого .
Предположим, что векторы
некомпланарны.
Но тогда существует параллелепипед,
построенный на этих векторах, объем
которого  ,
а это противоречит условию ,
а это противоречит условию .
Следовательно, предположение неверно,
и векторы
компланарны. .
Следовательно, предположение неверно,
и векторы
компланарны.
Билет
10.
Плоскость
в пространстве. Различные формы
уравнения плоскости. Простейшие
задачи.
|
Плоскость
в пространстве
|
|
Пусть
Мо(хо,
уо, zо)
– заданная точка в плоскости ,  =
(А; В; С) – вектор, перпендикулярный
плоскости ,
его называют нормальным
вектором плоскости,
и пусть М(х, у, z)
– произвольная точка плоскости
(рис. 43). Тогда =
(А; В; С) – вектор, перпендикулярный
плоскости ,
его называют нормальным
вектором плоскости,
и пусть М(х, у, z)
– произвольная точка плоскости
(рис. 43). Тогда   то
есть то
есть
|

|
(2.28)
|
(2.28)
– уравнение плоскости, проходящей
через данную точку перпендикулярно
данному вектору.
 Рис.
43 Рис.
43
Раскрыв
скобки и сгруппировав слагаемые,
получим  Обозначим Обозначим   уравнение
примет вид уравнение
примет вид

(2.29)
– общее уравнение плоскости.
Если
в этом уравнении А, В, С, Д 0,
то его можно привести к виду
|

|
(2.30)
|
(2.30)
– уравнение плоскости в отрезках
(аналогично (2.14)). Здесь а, в, с –
отрезки, отсекаемые плоскостью на
осях координат.
Пусть
заданы три точки в плоскости: М1(х1,
у1, z1),
М2(х2,
у2, z2),
М3(х3,
у3, z3),
и пусть М(х,
у, z)–произвольная_точка_плоскости_(рис.44).
Тогда    Эти
векторы компланарны (лежат в одной
плоскости), следовательно, их
смешанное произведение равно
нулю: Эти
векторы компланарны (лежат в одной
плоскости), следовательно, их
смешанное произведение равно
нулю:  или
через координаты или
через координаты
(2.31)
– уравнение плоскости, проходящей
через три данные точки.
 Рис.
44 Рис.
44
|
|
Неполные
уравнения плоскостей
|
|
Если
в уравнении плоскости  какие-либо
из коэффициентов равны нулю, то
получится неполное уравнение
плоскости. какие-либо
из коэффициентов равны нулю, то
получится неполное уравнение
плоскости.
Пусть,
например,  Уравнение
имеет вид Уравнение
имеет вид  и
определяет плоскость, проходящую
через начало координат (координаты
точки О(0; 0; 0) удовлетворяют
уравнению). и
определяет плоскость, проходящую
через начало координат (координаты
точки О(0; 0; 0) удовлетворяют
уравнению).
Пусть  Уравнение
имеет вид Уравнение
имеет вид  и
определяет плоскость, параллельную
оси Оz или проходящую через ось
Оz при и
определяет плоскость, параллельную
оси Оz или проходящую через ось
Оz при  Действительно,
тогда Действительно,
тогда  то
есть то
есть  а
плоскость а
плоскость
Пусть  Уравнение
имеет вид Уравнение
имеет вид  и
определяет плоскость, параллельную
плоскости Оуz или совпадающую
с ней при и
определяет плоскость, параллельную
плоскости Оуz или совпадающую
с ней при  Действительно, Действительно,  то
есть то
есть  а
плоскость а
плоскость  или или 
Аналогично
можно рассмотреть другие случаи.
|
|
Угол
между двумя плоскостями
|
|
Пусть
плоскости a1 и a2 заданы
соответственно уравнениями :

 где где   и и  –
нормальные векторы этих плоскостей
(рис. 45). Очевидно, –
нормальные векторы этих плоскостей
(рис. 45). Очевидно,  тогда
косинус угла между плоскостями тогда
косинус угла между плоскостями

 Рис.
45 Рис.
45
Если  то то  –
условие параллельности плоскостей. –
условие параллельности плоскостей.
Если  то то  то
есть то
есть  –
условие перпендикулярности
плоскостей. –
условие перпендикулярности
плоскостей.
|
|
|
Билет
8.
Декартовая
система координат на плоскости и в
пространстве. Формулы перехода от
одной сисетмы координат к другой.
(сдвиг начала координат, поворот осей)
Декартова
система координат в пространстве.
Декартовы
координаты в пространстве задаются
с
помощью точки начала координат и трёх
взаимно-перпендикулярных направленных
прямых.
Прямые занумерованы, задан единичный
отрезок. Положение любой точки в
пространстве однозначно определено
тремя числами: первое число – величина
проекции точки на первую ось, второе
– величина проекции на вторую ось,
третье – на третью.

Билет
11.
Нормальные
уравнения прямой на плоскости и
плоскости в пространстве. Отклонение
точки от прямой (плоскости). Задачи
решаемые с помощью отклонения.
1. Нормальное
уравнение прямой
      
где p -
длина перпендикуляра (нормали),
опущенного из начала координат на
прямую, а  -
угол наклона этого перпендикуляра к
оси Ox.
Чтобы привести общее уравнение
прямой Ax + By + C =
0 к нормальному виду, нужно все члены
его умножить на нормирующий
множитель -
угол наклона этого перпендикуляра к
оси Ox.
Чтобы привести общее уравнение
прямой Ax + By + C =
0 к нормальному виду, нужно все члены
его умножить на нормирующий
множитель     ,
взятый со знаком, противоположным
знаку свободного члена C. ,
взятый со знаком, противоположным
знаку свободного члена C.
2. Расстояние
точки A(x1, y1)
до прямой Ax + By + C =
0 есть длина перпендикуляра, опущенного
из этой точки на прямую. Она определяется
по формуле
   
Правило. Чтобы
определить расстояние точки A(x1, y1)
до прямой Ax + By + C =
0, нужно привести уравнение прямой к
нормальному виду, взять левую часть
полученного уравнения и подставить
в нее вместо текущих координат
координаты данной точки. Абсолютная
величина полученного числа и даст
искомое расстояние:
      
Расстояние
от точки до прямой
есть всегда величина положительная.
Кроме расстояния от точки до прямой,
рассматривается еще так называемое
отклонение точки от прямой.
Отклонение  данной
точки от данной прямой
есть расстояние от этой точки до
прямой, которому приписывается знак
плюс, если точка и начало координат
находятся по разные стороны от прямой,
и знак минус, если точка и начало
координат находятся по одну сторону
от прямой. данной
точки от данной прямой
есть расстояние от этой точки до
прямой, которому приписывается знак
плюс, если точка и начало координат
находятся по разные стороны от прямой,
и знак минус, если точка и начало
координат находятся по одну сторону
от прямой.
Расстояние
от точки до прямой есть абсолютная
величина отклонения этой точки от
прямой.
Найти
расстояние от начала координат до
прямой x + y -
2 = 0.
Решение.
Приведем
уравнение прямой к нормальному виду.
Нормирующий множитель
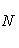  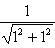    
В
нормальном виде уравнение прямой
запишется так:
      
Свободный
член в нормальном уравнении прямой,
взятый по абсолютной величине, дает
искомое расстояние   единицы. единицы.
|


 Рис.
17
Рис.
17 Рис.
23
Рис.
23 Рис.
24
Рис.
24
 Рис.
18
Рис.
18 Рис.
19
Рис.
19 Рис.
43
Рис.
43 Рис.
45
Рис.
45