Ризик портфеля в цьому разі є середньозваженою величиною ризику окремих проектів, а ваговими коефіцієнтами є частки цих проектів у портфелі.
Розглянемо приклад. Нехай проекти 1 і 2 мають такі характеристики «ризик-прибутковість» (таблиця 8.1).
Таблиця 8.1 – Характеристики проектів
|
1 |
2 |
E(Rj) |
15% |
20% |
j |
12% |
16% |
Визначити значення сподіваної прибутковості портфеля проектів E(Rp) і ризик портфеля p, якщо 12=+1.0. Побудувати графік залежності «ризик-прибутковість».
Підставимо значення сподіваної прибутковості проектів і ризиків проектів до формул (8.1) і (8.7):
,
.
Складемо таблицю для обчислення E(Rp) і p, маючи на увазі, що X2=1-X1.
Таблиця 8.2 – Розрахунок параметрів моделі
Х1 |
1.00 |
0.75 |
0.50 |
0.25 |
0 |
Х2 |
0 |
0.25 |
0.50 |
0.75 |
1.00 |
р |
12% |
13% |
14% |
15% |
16% |
E(Rp) |
15% |
16.25% |
17.50% |
18.75% |
20% |
За даними таблиці побудуємо графік E(RP) = F(P).
Рисунок 8.6 – Залежність параметрів «ризик-прибутковість»
Точка A відповідає портфелю, до якого входить лише проект 1, а точка B – портфелю, що складається тільки з проекту 2. Точки на відрізку AB відповідають портфелям, що складаються з різних часток проектів 1 і 2.
У цьому разі досягти ефекту зменшення ризику не вдається, тому що зі зниженням ризику знижується сподівана прибутковість портфеля.
Випадок 2. 12=-1.0.
Цей випадок відображає абсолютно від’ємну кореляцію між проектами 1 і 2. Підставляючи значення коефіцієнта кореляції 12=-1.0 у формулу (8.5), отримаємо:
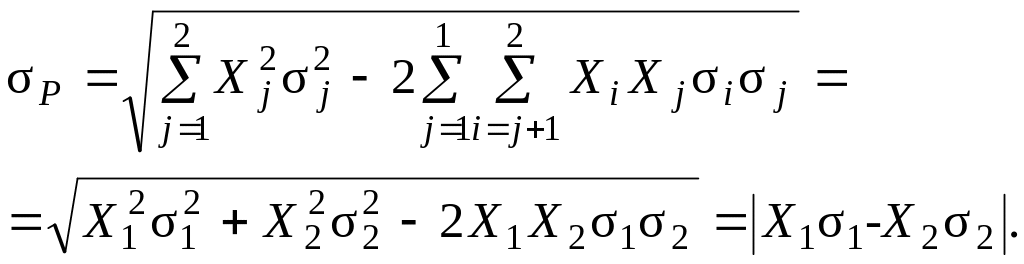(8.8)
У даному разі ризик портфеля проектів можна зробити нульовим, тобто:
,
,
,
.
(8.9)
Випадок 3. 12=0.
Цей випадок описує відсутність будь-якого взаємозв’язку між сподіваними нормами прибутковості проектів, тобто формування прибутковості одного проекту не пов’язано з формуванням прибутковості другого проекту. Підставивши значення 12=0 в формулу (8.5) обчислення стандартного відхилення портфеля проектів, отримаємо:
.
(8.10)
Ця функція досягає свого мінімуму, якщо:
;
.
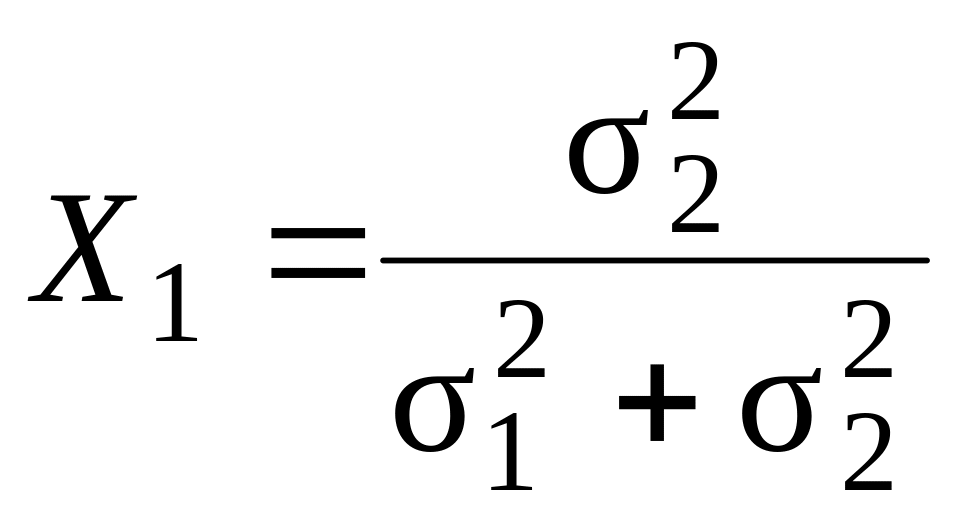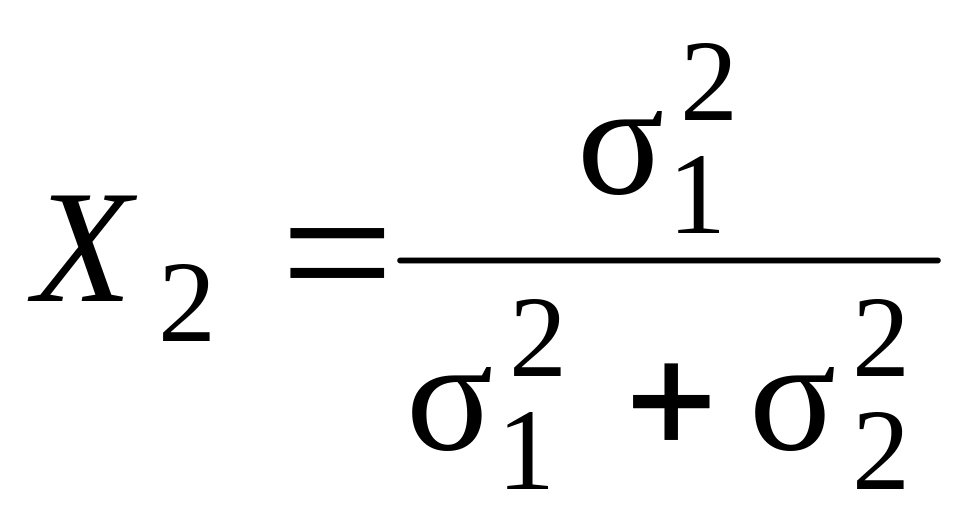(8.11)
Мінімальне значення ризику портфеля можна обчислити також з формули:
.
(8.12)
Контрольні запитання
1. Дайте визначення портфеля інвестицій.
2. Наведіть та поясніть формулу розрахунку сподіваних доходів портфеля інвестицій.
3. Що вимірює коваріація між двома проектами?
4. Від знака якого коефіцієнта залежить знак коваріації?
5. Що означають позитивна, негативна та нульова коваріації?
6. Як обчислити сподівану вартість та стандартне відхилення портфеля інвестицій? Які дані для цього потрібно мати ?
7. Як обчислити сподівану вартість та стандартне відхилення портфеля інвестицій з мінімальним ризиком? Які дані для цього слід мати?
8. Визначте поняття ефективного портфеля проектів (цінних паперів). Яка комбінація проектів (паперів) у портфелі може вважатися неефективною ?
9. Наведіть алгоритм визначення ефективного кордону (множини) портфеля з двох інвестиційних проектів.
10. Як визначити оптимальний портфель активів (проектів)?