Звідси випливає перша важлива властивість кривих байдужості: Всі портфелі, що лежать на одній заданій кривій байдужості, є рівноцінними для інвестора.

Наслідком цієї властивості є те, що криві байдужості не можуть перетинатися.

Другою важливою властивістю кривих байдужості є ось що:

Інвестор вважатиме будь-який портфель, що лежить на кривій байдужості, розташованій вище і лівіше, привабливішим, ніж будь-який портфель, що лежить на кривій байдужості, розташованій нижче і правіше.

Кожен інвестор має теоретично нескінченну кількість кривих байдужості. Це означає, що як би не були розташовані дві криві байдужості на графіку, завжди є можливість побудови третьої кривої, що лежатиме чи між ними, чи вище, чи нижче.

Інвестор, який робить вибір між двома ідентичними у всьому портфелями, вибирає портфель з більшою очікуваною прибутковістю.

У портфельній теорії Марковіца робиться два припущення – про ненасичуваність інвестора і про запобігання інвестором ризику.

Припущення про ненасичуваність означає, що інвестор завжди віддає перевагу більш високому рівню добробуту. Наприклад, коли є два портфелі А і Е з однаковими стандартними відхиленнями, то інвестор вибере портфель Е з більшою сподіваною прибутковістю (рисунок 8.1).

Припущення про запобігання інвестором ризику означає, що він вибирає менш ризикований портфель. Якщо інвестору треба вибирати між портфелями, що мають однаковий рівень очікуваної прибутковості (на рисунку 8.1 портфелі D і F), та водночас мають різні стандартні відхилення як міри ризикованості портфелів, то він вибирає портфель з нижчим стандартним відхиленням – портфель F.

Що означає, що інвестор уникає ризику? Те, що інвестор, не захоче вибрати «чесну гру», за якою, за визначенням, сподівана винагорода дорівнює 0. Інвестор, який уникає ризику, інстинктивно уникатиме цієї гри. Це пояснюється тим, що «кількість розчарування» при потенційному програші в нього виявляється вищою, ніж «кількість задоволення» при потенційному виграші.

Ці два припущення про ненасичуваність і уникнення ризику є причиною опуклості кривої байдужості.

Незважаючи на припущення, що всі інвестори уникають ризику, міра уникнення в них неоднакова. Наприклад, інвестори, які уникають ризику високою мірою, матимуть більш крутіший нахил кривих байдужості, ніж ті, які уникають нижчою мірою.

Припущення, що інвестор уникає ризику, є цілком резонним, але не є необхідним. Замість цього можна зробити припущення про азартність і нейтральність щодо ризику.

Якщо інвестор азартний і зіткнеться з «чесною грою», то він вважатиме за краще взяти в ній участь, оскільки він отримує більше задоволення від виграшу, ніж розчарування від програшу. При виборі двох інвестиційних портфелів азартний інвестор за однакової очікуваної прибутковості вибере той, що має більше стандартне відхилення.

Є підстави передбачити, що крива байдужості азартного інвестора (рисунок 8.2) матиме негативний нахил, тобто він віддасть перевагу портфелю, який знаходиться вище і правіше від інших (точка В), що пояснюється бажанням отримати максимальний прибуток при максимальному ризику.

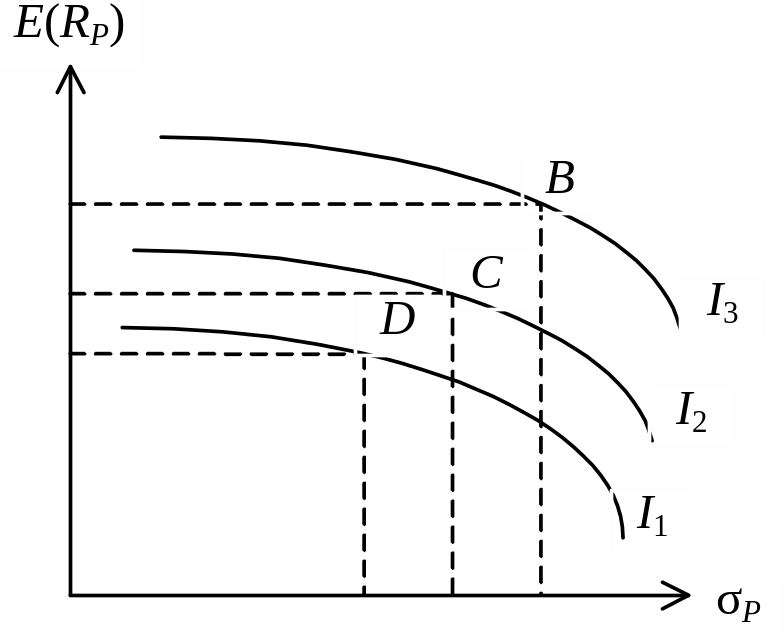
Рисунок 8.2 – Графік кривих байдужості «азартного» інвестора

Випадок нейтральності до ризику знаходиться між випадками уникнення ризику та азартності. Нейтральному до ризику інвестору все одно, брати участь у «чесній грі» чи ні. Це означає, що ризик, чи радше стандартне відхилення не є важливим для інвестора при оцінці портфеля. Крива байдужості такого інвестора буде горизонтальною лінією (рисунок 8.3). Такий інвестор вважає за ліпше вибирати портфелі, розташовані на кривих байдужості більш високо, тобто мають максимальну сподівану прибутковість (точка В).

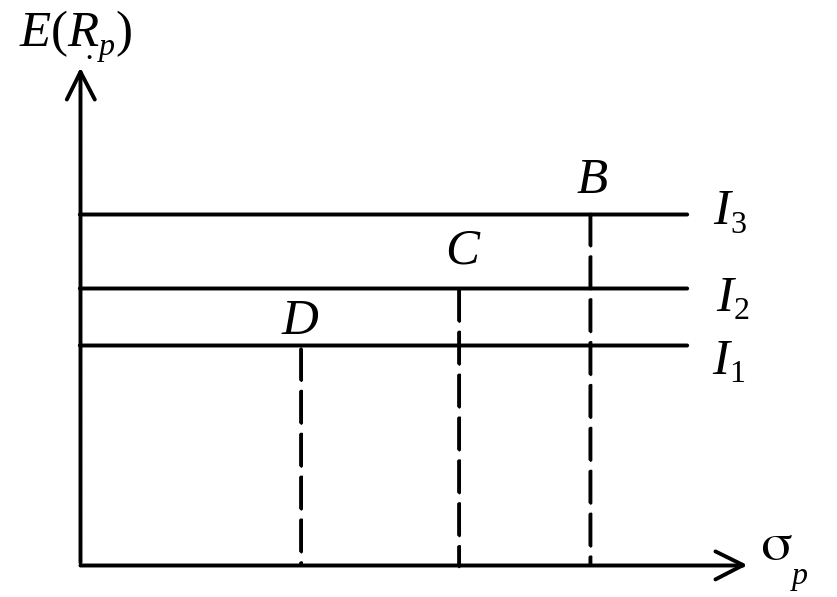
Рисунок 8.3 – Графік кривих байдужості інвестора, нейтрального до ризику

Припустимо, що розглядаються певні комбінації можливих інвестиційних проектів (ЦП) як портфелі. Кожен інвестиційний проект (ЦП) має сподівану прибутковість і ризик, що вимірюється стандартним відхиленням.

Для того, щоб оцінити ці комбінації, необхідно визначити сподівану прибутковість і стандартне відхилення кожного портфеля інвестицій.

Сподівана прибутковість портфеля інвестицій (Е(R_P)) обчислюється за рівнянням (8.1):

, (8.1)

де X_j – частка первинної вартості інвестицій, вкладена в проект j;

E(R_j) – сподівана прибутковість j-го проекту;

n – кількість проектів.

Для визначення стандартного відхилення портфеля інвестицій _p вводиться поняття коваріації між парою інвестиційних проектів.

Коваріація між парою інвестиційних проектів (ЦП) вимірює вплив на дисперсію портфеля через ефект їхньої взаємодії, тобто кореляцію і їх відповідні стандартні відхилення.

Коваріація між двома проектами (ЦП) дорівнює добутку парного коефіцієнта кореляції і стандартних відхилень кожного проекту (8.2):

. (8.2)

Коефіцієнт кореляції _ij вимірює існування і силу взаємозв’язку між двома проектами (ЦП). Коефіцієнт кореляції приймає значення -1.0_ij+1.0.