
Билеты по ан. геометрии / 7
.docДекартова система координат.
Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.
Вектор
![]() назовем радиус- вектором точки М. Если
в пространстве задать некоторый базис,
то точке М можно сопоставить некоторую
тройку чисел – компоненты ее радиус-
вектора.
назовем радиус- вектором точки М. Если
в пространстве задать некоторый базис,
то точке М можно сопоставить некоторую
тройку чисел – компоненты ее радиус-
вектора.
Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки
А(x1,
y1,
z1),
B(x2,
y2,
z2),
то
![]() =
(x2
– x1,
y2
– y1,
z2
– z1).
=
(x2
– x1,
y2
– y1,
z2
– z1).
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Пример.
Даны векторы![]() (1;
2; 3),
(1;
2; 3),
![]() (-1;
0; 3),
(-1;
0; 3),
![]() (2;
1; -1) и
(2;
1; -1) и
![]() (3;
2; 2) в некотором базисе. Показать, что
векторы
(3;
2; 2) в некотором базисе. Показать, что
векторы
![]() ,
,
![]() и
и
![]() образуют
базис и найти координаты вектора
образуют
базис и найти координаты вектора
![]() в этом базисе.
в этом базисе.
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
 линейно
независимы.
линейно
независимы.
Тогда
![]() .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.


![]()
 Для решения этой
системы воспользуемся методом Крамера.
Для решения этой
системы воспользуемся методом Крамера.
1
=

![]() ;
;
2
=

![]()
3
=

![]()
Итого, координаты
вектора
![]() в
базисе
в
базисе
![]() ,
,
![]() ,
,
![]() :
:
![]() { -1/4, 7/4, 5/2}.
{ -1/4, 7/4, 5/2}.
В открывшемся окне программы введите координаты векторов и нажмите Enter.
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple ( Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Длина
вектора в координатах
определяется как расстояние между
точками начала и конца вектора. Если
заданы две точки в пространстве А(х1,
y1,
z1),
B(x2,
y2,
z2),
то
![]() .
.
Если точка М(х, у, z) делит отрезок АВ в соотношении /, то координаты этой точки определяются как:
![]()
В частном случае координаты середины отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Скалярное произведение векторов.
Определение.
Скалярным произведением векторов
![]() и
и
![]() называется число, равное произведению
длин этих сторон на косинус угла между
ними.
называется число, равное произведению
длин этих сторон на косинус угла между
ними.

![]()
![]() =
= ![]()
![]() cos
cos
Свойства скалярного произведения:
-

 =
=  2;
2; -

 = 0, если
= 0, если

 или
или
 =
0 или
=
0 или
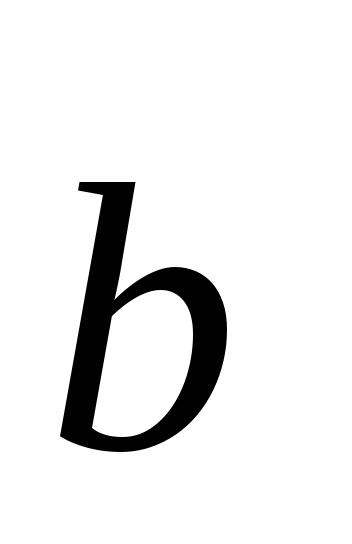 = 0.
= 0. -

 =
=
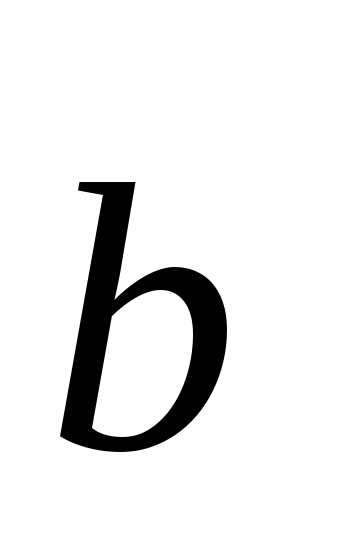
 ;
; -
 (
( +
+ )
=
)
=

 +
+

 ;
; -
(m
 )
) =
=
 (m
(m )
= m(
)
= m(
 );
);
Если рассматривать
векторы
![]() в
декартовой прямоугольной системе
координат, то
в
декартовой прямоугольной системе
координат, то

![]()
![]() = xa
xb
+ ya
yb
+ za
zb;
= xa
xb
+ ya
yb
+ za
zb;
 Используя
полученные равенства, получаем формулу
для вычисления угла между векторами:
Используя
полученные равенства, получаем формулу
для вычисления угла между векторами:
![]() ;
;
Пример.
Найти (5![]() + 3
+ 3![]() )(2
)(2![]() -
-
![]() ),
если
),
если
![]()
10![]()
![]() -
5
-
5![]()
![]() +
6
+
6![]()
![]() -
3
-
3![]()
![]() = 10
= 10![]() ,
,
т.к.
![]() .
.
Пример.
Найти угол между векторами
![]() и
и
![]() ,
если
,
если
![]()
![]() .
.
Т.е.
![]() = (1, 2, 3),
= (1, 2, 3),
![]() =
(6, 4, -2)
=
(6, 4, -2)
![]()
![]() =
6 + 8 – 6 = 8:
=
6 + 8 – 6 = 8:
![]() .
.
cos
=
![]()
Пример.
Найти скалярное произведение (3![]() - 2
- 2![]() )(5
)(5![]() - 6
- 6![]() ),
если
),
если
![]()
15![]()
![]() -
18
-
18![]()
![]() -
10
-
10![]()
![]() +
12
+
12![]()
![]() = 15
= 15![]()
+ 1236 = 240 – 336 + 432 = 672 – 336 = 336.
Пример.
Найти угол между векторами
![]() и
и
![]() ,
если
,
если
![]()
![]() .
.
Т.е.
![]() = (3, 4, 5),
= (3, 4, 5),
![]() =
(4, 5, -3)
=
(4, 5, -3)
![]()
![]() =
12 + 20 - 15 =17 :
=
12 + 20 - 15 =17 :
![]() .
.
cos
=
![]()
Пример.
При каком m
векторы
![]() и
и
![]() перпендикулярны.
перпендикулярны.
![]() =
(m,
1, 0);
=
(m,
1, 0);
![]() =
(3, -3, -4)
=
(3, -3, -4)
![]() .
.
Пример.
Найти скалярное произведение векторов
![]() и
и
![]() ,
если
,
если
![]()
(![]() )(
)(![]() )
=
)
=
![]()
![]()
![]() =
10 +
=
10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
