2.2.1. Определение параметров газа в переходных точках цикла.

Найдем объем v₁ из уравнения Клапейрона:

(2.76)

Для данной точки объем будет равен:

(2.77)

Где R – газовая постоянная, кДж/кг_*К;

Т₁ – температура в точке 1, К;

р₁ – давление в точке 1, Па.

Найдем внутреннюю энергию u₁.

Величина внутренней энергии газа зависит, как от скорости движения молекул и атомов, так и от расстояния между ними. Скорость движения микрочастиц вещества зависит от температуры тела, а силы взаимодействия между ними - от удельного объема. Поэтому внутреннюю энергию можно представить в виде:

(2.78)

где с_v – изохорная теплоемкость газа, кДж/кгК.

Вычислим энтальпию h₁.

Энтальпия газа так же, как и внутренняя энергия, зависит только от температуры. Следовательно, энтальпия h₁ рассчитывается по формуле:

(2.79)

где с_р – изобарная теплоемкость газа, кДж/кгК.

Найдем энтропию s₁.

В уравнении первого закона термодинамики dq = du + pdv только du является полным дифференциалом внутренней энергии u. Введением множителя 1/Т можно привести это уравнение к уравнению в полных дифференциалах:

(2.80)

где ds – полный дифференциал параметра s, то есть энтропии.

Для идеальных газов pv = RT, du = c_vdT, поэтому

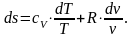(2.81)

После интегрирования (2.78) получаем расчетную формулу для определения энтропии:

(2.82)

Где v₁ – объем точки 1, м³/кг;

v_н – объем при нормальных условиях, м³/кг.

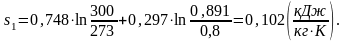
Определим параметры газа в точке 2

По изобаре 2-3 определяем, что Р₂=Р₃, отсюда р₂=0,9 МПа.

Из условия, что процесс 1-2 является адиабатным, имеем:

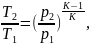(2.83)

Получаем:

(2.84)

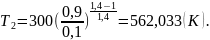
Объём найдём из уравнения Клайперона-Менделеева:

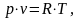(2.85)

Для данной точки объем будет равен:

(2.86)

Где Т₂ – температура в точке 2, К;

р₂ – давление в точке 2, Па.

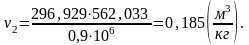
Найдем внутреннюю энергию u₂ аналогично u₁:

(2.87)

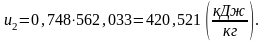
Определим энтальпию h₂ аналогично h₁:

(2.88)

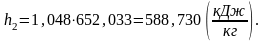
Найдем энтропию s₂ аналогично s₁:

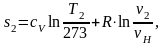(2.89)

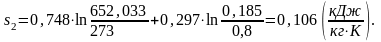
Определим параметры газа в точке 3

Найдем объем v₃ аналогично v₁:

(2.90)

.

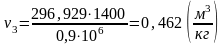Вычислим внутреннюю энергию u₃ аналогично u₁:

(2.91)

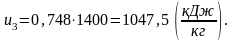
Найдем энтальпию h₃ аналогично h₁:

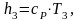(2.92)

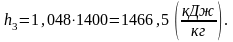
Вычислим энтропию s₃ аналогично s₁:

(2.93)

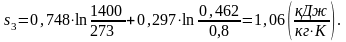
Определим параметры газа в точке 4

Так как процесс 3-4 является адиабатным:

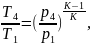(2.94)

Отсюда

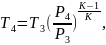(2.95)

.

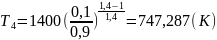Вычислим объем v₄ аналогично v₁:

(2.96)

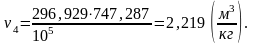
Найдем внутреннюю энергию u₄ аналогично u₁:

(2.97)

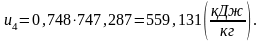
Определим энтальпию h₄ аналогично h₁:

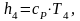(2.98)

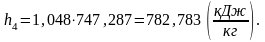
Вычислим энтропию s₄ аналогично s₁:

(2.99)