1.2.3. Определение работы и изменения параметров: внутренней энергии, энтальпии и энтропии.

Вычислим изменение внутренней энергии ∆u_1-2 .

Изменение внутренней энергии можно рассчитать по формуле:

(1.48)

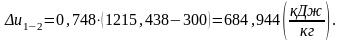
Определим изменение энтальпии ∆h_1-2.

Изменение внутренней энергии ∆u_1-2, можно рассчитать, как и изменение энтальпии ∆h_1-2:

(1.49)

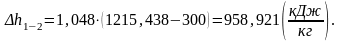
Вычислим изменение энтропии ∆s_1-2.

Аналогично изменению внутренней энергии и изменению энтальпии можно рассчитать изменение энтропии ∆s_1-2.

(1.50)

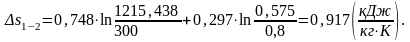
Найдём работу l_1-2 в данном процессе.

Для политропного процесса работа рассчитывается по формуле:

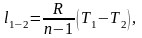(1.51)

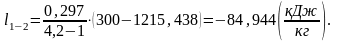
Таблица 1.4 – Результаты начальных и конечных параметров, тепло, работа, изменение параметров.

Неизвестные параметры	Р1, МПа	Т1, К
Полученный результат	0,1	300	0,891	224,464	314,25	0,102

Продолжение таблицы 1.4 – Результаты начальных и конечных параметров, тепло, работа, изменение параметров.

Неизвестные параметры	Р2, МПа	Т2, К
Полученный результат	0,627	1215,438	0,575	909,408	1273,171	1,019

Окончание таблицы 1.4 – Результаты начальных и конечных параметров, тепло, работа, изменение параметров.

Неизвестные параметры
Полученный результат	600	-84,944	958,921	684,944	0,917

Таблица 1.5 - Промежуточные точки для p,v – диаграммы.

Точки	Давление р, Па	Удельный объём
A	164832	0,791
B	290787	0,691
C	375964	0,650
D	526195	0,600
E	585232	0,585

Таблица 1.6– Промежуточные точки для Т, S- диаграммы.

Точки	Температура Т, К	Энтропия
A	439	0,352
B	677	0,636
C	823	0,764
D	1063	0,932
E	1153	0,985

Вывод: политропный процесс является обобщающим для всех процессов. При расчётах политропного процесса требуется знание политропы.

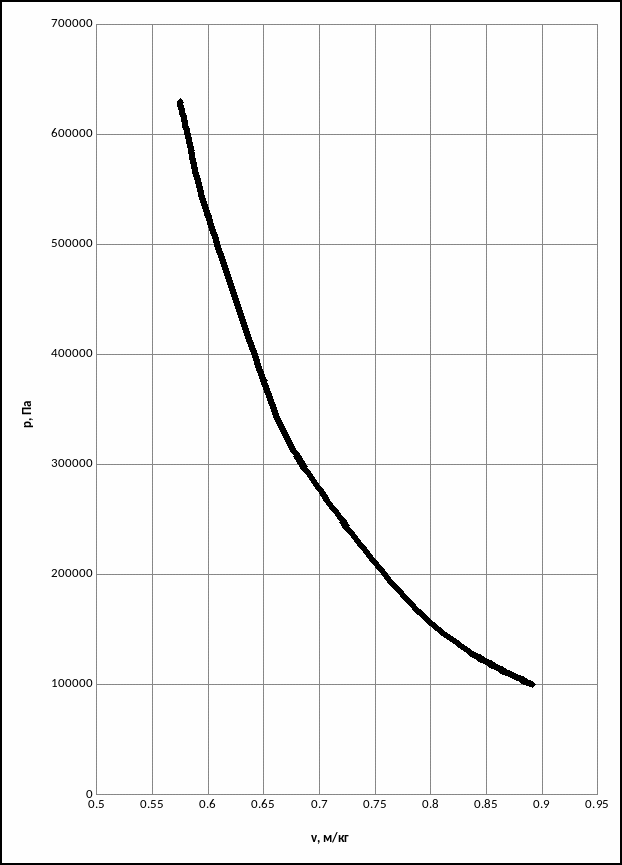
Рисунок 1.3. – диаграмма в p,v- координатах.

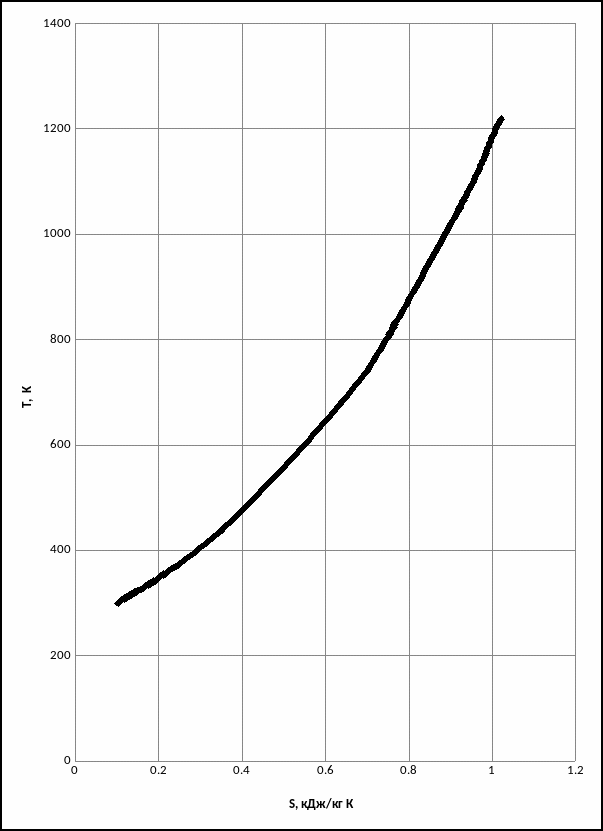
Рисунок 1.4 – диаграмма в T,S – координатах.

2. Газовые циклы.

Рассчитать теоретические циклы ДВС и ГТУ в соответствии с исходными данными.

2.1. Задача 1. Определить:

- параметры газа в переходных точках цикла ДВС (результаты расчёта свести в табл.);

- тепло, работу и изменение параметров ∆u, ∆h, ∆s, в каждом процессе;

- полезную работу, подведённое и отведенное тепло в цикле ДВС, его КПД (двумя способами);

- построить цикл в масштабе в диаграммах p,v и T,s.

Дано: "СИ"

Рабочее тело – N₂

подвод тепла – смешанный

р₁ = 0.1 МПа

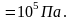
Т₁ = 300 К

 = 21,0

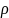=1,28

λ=2.05

Найти:

v₁, u₁, h₁, s₁, p₂, T₂, v₂, u₂, h₂,

s₂, p_z, T_z, v_z, u_z, h_z, s_z, p_3, T₃, v₃,

u₃, h₃, s₃, p₄, T₄, v₄, u₄, h₄, s₄,

q_1-2, l_1-2, ∆u_1-2, ∆h_1-2, ∆s_1-2, q_2-z,

l_2-z, ∆u_2-z, ∆h_2-z, ∆s_2-z, q_z-3, l_z-3,

∆u_z-3, ∆h_z-3, ∆s_z-3, q_3-4, l_3-4,

∆u_3-4, ∆h_3-4, ∆s_3-4, q_4-1, l_4-1,

∆u_4-1, ∆h_4-1, ∆s_4-1, l, q₁, q₂, _t.

Решение:

Для расчетов неизвестных параметров необходимо рассчитать газовую постоянную. Газовая постоянная является индивидуальной для каждого газа, то есть зависит от молекулярной массы газа и рассчитывается по формуле:

(2.1)

где _см - это кажущаяся молекулярная масса, она зависит от пропорции компонентов, из которых состоит смесь газа.

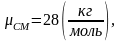
Для воздуха газовая постоянная будет равна:

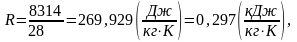
Так же понадобится для расчетов изобарная (с_р) и изохорная (с_v) теплоемкости, показатель адиабаты и объем при нормальных условиях. Так как данный газ N₂ – двухатомный, следовательно, изобарная теплоемкость равна:

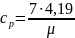, (2.2)

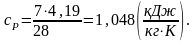
а изохорная теплоемкость равна:

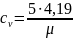, (2.3)

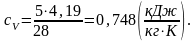
Показатель адиабаты равен:

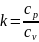, (2.4)

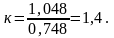
Объем при нормальных условиях будет равен:

, (2.5)