1.2.1. Определение недостающих начальных параметров.

Определим начальный объем v₁

Из уравнения Клапейрона:

pv=RT , (1.31)

можно найти объем, выразив его.

Для данного случая начальный объем будет равен:

(1.32)

где R – газовая постоянная, кДж/кгК;

Т₁ – начальная температура, К;

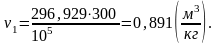р₁ – начальное давление, Па.

Определим начальную внутреннюю энергию u₁

Величина внутренней энергии газа зависит как от скорости движения молекул и атомов, так и от расстояния между ними. Скорость движения микрочастиц вещества зависит от температуры тела, а силы взаимодействия между ними – от удельного объема. Поэтому внутреннюю энергию можно представить в виде:

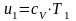, (1.33)

где с_v – изохорная теплоемкость газа, кДж/кгК;

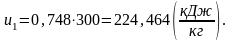
Энтальпия h₁ в начале процесса.

Энтальпия газа так же, как и внутренняя энергия, зависит только от температуры. Следовательно, энтальпия h₁ в начале процесса рассчитывается по формуле:

, (1.34)

где с_р – изобарная теплоемкость газа, кДж/кгК;

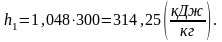
Определим энтропию s₁ в начале процесса.

В уравнении первого закона термодинамики dq = du + pdv только du является полным дифференциалом внутренней энергии u. Введением множителя 1/Т можно привести это уравнение к уравнению в полных дифференциалах:

(1.35)

где ds – полный дифференциал параметра s, то есть энтропии.

Для идеальных газов pv = RT, du = c_vdT, поэтому

, (1.36)

После интегрирования (1.36) получаем расчетную формулу для определения энтропии:

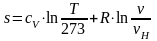, (1.37)

где v – начальный объем, м³/кг.

Согласно формуле (1.37) энтропию s₁ в данном случае рассчитаем по формуле:

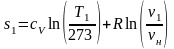, (1.38)

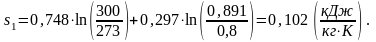
1.2.2. Определение недостающих конечных параметров.

Определим конечную температуру Т₂.

Так как известно количество тепла q и начальная температура Т₁, можно найти конечную температуру Т₂.

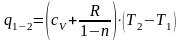, (1.39)

Из формулы (1.39) температура Т₂ будет равна:

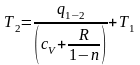, (1.40)

где q_1-2 – подводимое тепло, кДж/кг;

n – показатель политропы.

.

Определим конечное давление р₂.

Давление р₂ в конце процесса найдем из соотношения параметров:

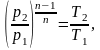(1,41)

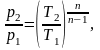(1.42)

Отсюда давление р₂ будет равно:

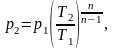(1.43)

где Т₂ – конечная температура, К.

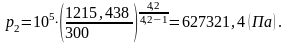
Определим конечный объем v₂.

Из формулы (1.6) для данного случая найдем конечный объем:

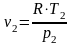, (1.44)

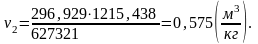
Найдём конечную внутреннюю энергию u₂.

Аналогично u₁ найдем конечную внутреннюю энергию u₂ по формуле:

(1.45)

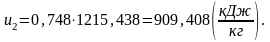
Определим энтальпию h₂ в конце процесса.

Аналогично h₁ найдем энтальпию h₂ в конце процесса по формуле:

(1.46)

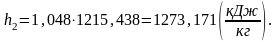
Определим энтропию s₂ в конце процесса.

Аналогично s₁ находим энтропию s₂ в конце процесса по формуле:

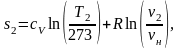(1.47)

где v₂ – конечный объем, м³/кг.