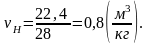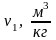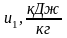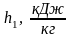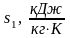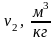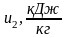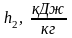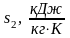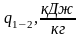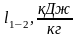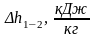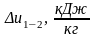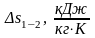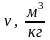1.1.2. Определение недостающих конечных параметров.

Определим конечную температуру Т₂.

Температуру Т₂ найдем из соотношения между параметрами политропного процесса:

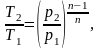(1.13)

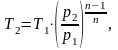(1.14)

где Т₂ – конечная температура, К;

р₂ – конечное давление, Па;

n – показатель политропы.

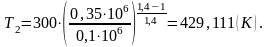
Найдём конечный объем v₂.

Из формулы (1.5) для данного случая найдем конечный объем v₂:

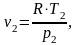(1.15)

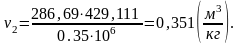
Определим конечную внутреннюю энергию u₂.

Аналогично u₁ найдем конечную внутреннюю энергию u₂ по формуле:

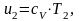(1.16)

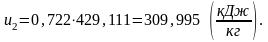
Определим энтальпию h₂ в конце процесса.

Аналогично h₁ найдем энтальпию h₂ в конце процесса по формуле:

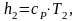(1.17)

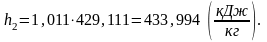
Найдём энтропию s₂ в конце процесса.

Аналогично s₁ находим энтропию s₂ в конце процесса по формуле:

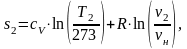(1.18)

где v₂ – конечный объем, м³/кг,

1.1.3. Определение тепла, работы и изменения параметров внутренней энергии, энтальпии и энтропии.

Определим тепло q_1-2 в данном процессе.

Количество тепла в политропном процессе рассчитывается по формуле:

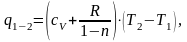(1.19)

Вычислим работу l_1-2 в данном процессе.

Для политропного процесса работа рассчитывается по формуле:

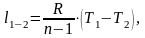(1.20)

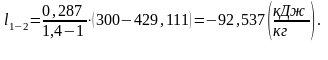
Определим изменение внутренней энергии ∆u_1-2 .

Изменение внутренней энергии можно рассчитать по формулам:

(1.21)

(1.22)

∆u_1-2 находим по формуле (1.22):

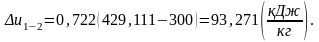
Определим изменение энтальпии ∆h_1-2.

Аналогично изменение внутренней энергии ∆u_1-2 можно рассчитать изменение энтальпии ∆h_1-2 по формулам:

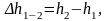(1.23)

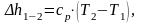(1.24)

∆h_1-2 находим по формуле (1.24):

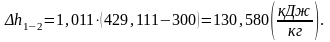
Определим изменение энтропии ∆s_1-2.

Как и изменение внутренней энергии, изменение энтропии ∆s_1-2 можно расчитать:

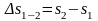, (1.25)

или

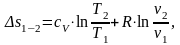(1.26)

∆s_1-2 находим по формуле (1.26):

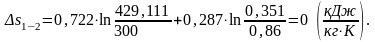
Все ответы приведены в таблице 1.1

Таблица 1.1 – Результаты начальных и конечных параметров, тепло, работа, изменение параметров.

Неизвестные параметры	Р1, МПа	Т1, К
Полученный результат	0,1	300	0,86	216,724	303,414	0,099

Продолжение таблицы 1.1 – Результаты начальных и конечных параметров, тепло работа, изменение параметров.

Неизвестные параметры	Р2, МПа	Т2, К
Полученный результат	0,35	429,111	0,351	309,995	433,994	0,101

Окончание таблицы 1.1 – Результаты начальных и конечных параметров, тепло, работа, изменение параметров.

Неизвестные параметры
Полученный результат	0	-92,537	130,580	93,271	0

Таблица 1.2 - Промежуточные точки для p,v – диаграммы.

Точки	Давление р,МПа	Удельный объём
A	0,119	0,76
B	0,145	0,66
C	0,182	0,56
D	0,24	0,46
E	0,292	0,4

Т,s – диаграмму строим по двум точкам: 1и 2.

Вывод: Адиабатный процесс носит частный характер, так как здесь накладывается ограничение: изменение количества тепла в процессе равно нулю.

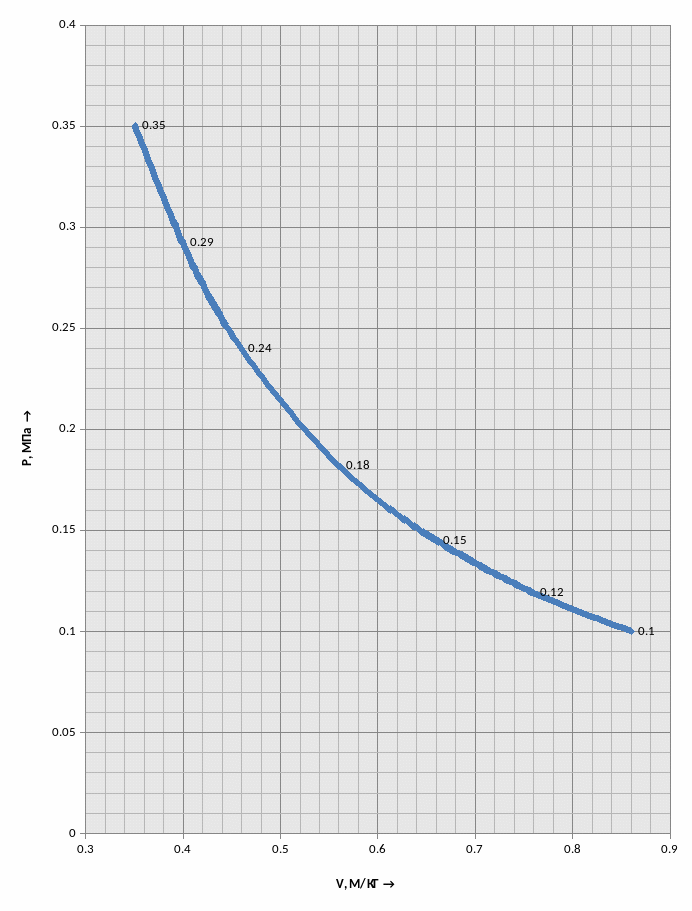
Рисунок 1.1.- Диаграмма в p,v – координатах.

Рисунок 1.2. – Диаграмма в T,S – координатах.

1 .2. Задача 2. В процессе 1-2 с показателем политропы n к 1 кг газа с начальными параметрами р₁ = 0,1МПа, Т₁ = 300 К подводится тепло q. Определить недостающие начальные параметры v_1, u_1, h_1, s_1, конечные параметры р₂, Т₂, v₂, u₂, h₂, s₂, изменение параметров в процессе ∆u_1-2, ∆h_1-2, ∆s_1-2 и работу l_1-2. Построить процесс в p, v – и T, s – диаграммах.

Дано: "СИ"

газ СО

процесс

политропный

Т₁ = 300 К

р₁ = 0.1 МПа .

q = 600 кДж/кг

n = 4,2

m =1 кг

Найти:

v₁, u₁, h₁, s₁, р₂,

T₂, v₂, u₂, h₂, s₂,

l_1-2, ∆u_1-2, ∆h_1-2,

∆s_1-2.

Решение:

Для расчетов неизвестных параметров необходимо рассчитать газовую постоянную. Газовая постоянная является индивидуальной для каждого газа, то есть зависит от молекулярной массы газа и рассчитывается по формуле:

(1.27)

где _см – это кажущаяся молекулярная масса, она зависит от пропорции компонентов, из которых состоит смесь газа. В данном случае имеется газ СО, и для него газовая постоянная будет равна:

.

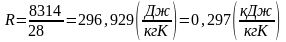Так же понадобится для расчетов изобарная (с_р) и изохорная (с_v) теплоемкости. Так как данный газ - двухатомный, следовательно изобарная теплоемкость равна:

(1.28)

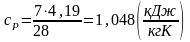
а изохорная теплоемкость равна:

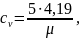(1.29)

.

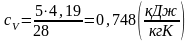Объем при нормальных условиях будет равен:

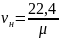, (1.30)