4. Циклы трансформаторного тепла

4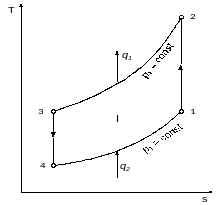 .1. Задача 1. В газовой холодильной установке в качестве рабочего тела используется воздух с давлением перед компрессором р₁ = 0.1 МПа. Определить затрачиваемую в теоретическом цикле работу l, удельную холодопроизводительность q₂, и холодильный коэффициент .

Дано: "СИ"

р₁ = 0,1 МПа

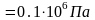
р₂ = 0,45 МПа

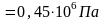
t₁ = -9,5 ^оС

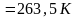
t₃ = 15 ^оС

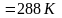
q₂, l,  – ?

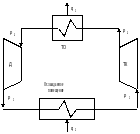
График зависимости S(T)

Решение:

Для того, чтобы найти затрачиваемую в теоретическом цикле работу, удельную холодопроизводительность и холодильный коэффициент нам необходимо рассчитать молекулярную массу вещества, изохорную и изобарную теплоемкости и показатель адиабаты.

Итак, молекулярная масса воздуха будет равна:

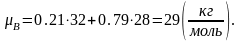
Так как воздух – двухатомный газ, тогда изобарная теплоемкость будет находиться следующим образом:

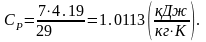
Изохорная теплоемкость будет равна:

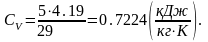
Показатель адиабаты будет равен отношению изобарной теплоемкости к изохорной:

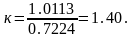
4.1.1. Расчет удельной холодопроизводительности в цикле.

Удельную холодопроизводительность рассчитаем по формуле:

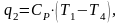(4.1)

где С_Р – изобарная теплоемкость, кДж/кгК;

Т₁ – температура в точке 1, К;

Т₄ – температура в точке 4, К.

Так как процессы 2 – 3 и 4 – 1 — p = const, тогда следует, что 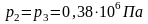и .

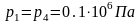Тогда можно найти температуры Т₂ и Т₄.

Температуру Т₂ можно рассчитать по формуле:

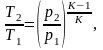(4.2)

отсюда Т₂ будет равна:

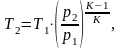(4.3)

Где р₂ – давление в точке 2, Па;

р₁ – давление в точке 1, Па;

к – показатель адиабаты.

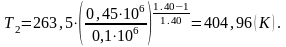
Температуру Т₄ можно рассчитать по формуле:

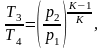(4.4)

откуда Т₄ будет равна:

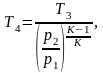(4.5)

где Т₃ – температура в точке 3, К.

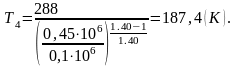
Теперь рассчитаем удельную холодопроизводительность:

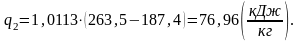
4.1.2. Расчет затраченной работы в цикле.

Затраченная работа рассчитывается по формуле:

(4.6)

где 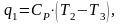кДж/кг;

кДж/кг.

Подставив q₁ и q₂ получим следующую формулу:

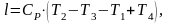(4.7)

где Т₂ – температура в точке 2, К;

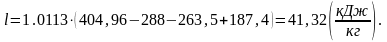
4.1.3. Расчет холодильного коэффициента в цикле.

Холодильный коэффициент можно рассчитать по формуле:

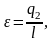(4.8)

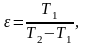(4.9)

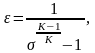(4.10)

где 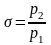– степень повышения давления в компрессоре.

Итак, рассчитаем холодильный коэффициент по формуле (4.8):

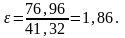
Рассчитаем холодильный коэффициент по формуле (4.9):

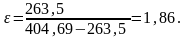
Теперь рассчитаем холодильный коэффициент по формуле (4.10):

Результаты сведены в таблице4.1.

Таблица 4.1

q2, кДж/кг	l, кДж/кг	ε
76,96	41,32	1,86

Вывод: более низкий холодильный коэффициент цикла газовой холодильной установки объясняется необратимостью теплообмена в изобарных процессах отвода (2 - 3) и подвода (4 - 1) теплоты к рабочему телу, так как эти процессы протекают при конечной разности температур.

4.2. Задача 2. Парокомпрессорная холодильная установка работает на хладоагенте R12 при температуре испарения t_И, ^оС и температуре конденсации t_К, ^оС. После сжатия в компрессоре пар сухой насыщенный. Расширение сконденсированного фреона осуществляется в дросселе. Определить холодильный коэффициент установки, построить циклы в диаграммах T, s и ln p, h.

Дано: "СИ"

Х₂=1 (сух. пар) График зависимости S(T)

t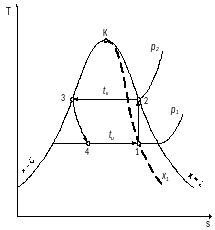 _И = -14,5 ^оС

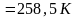
t_К = 26 ^оС

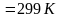
ε – ?

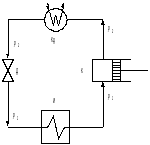
Решение:

Холодильный коэффициент рассчитывается по формуле:

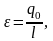(4.11)

где q ₀ – удельная холодопроизводительность, кДж/кг;

l – затраченная работа, кДж/кг.

Удельная холодопроизводительность будет равна:

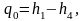(4.12)

Где h₁ – энтальпия в точке 1, кДж/кг;

h₄ – энтальпия в точке 4, кДж/кг.

Затраченная работа будет равна:

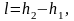(4.13)

Где h₂ – энтальпия в точке 2, кДж/кг.

Подставим выражения (4.12) и (4.13) в формулу (4.11) и получим:

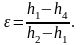(4.14)

По ln р, h – диаграмме находим нужные энтальпии:

h₁ = 564 кДж/кг;

h₂ = 585 кДж/кг;

h₃ = h₄ = 444 кДж/кг.

Подставим значения энтальпий в формулу (4.14) и рассчитаем холодильный коэффициент:

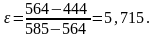
Вывод: холодильный коэффициент паровой компрессорной холодильной установки значительно выше, чем у газовых холодильных машин.

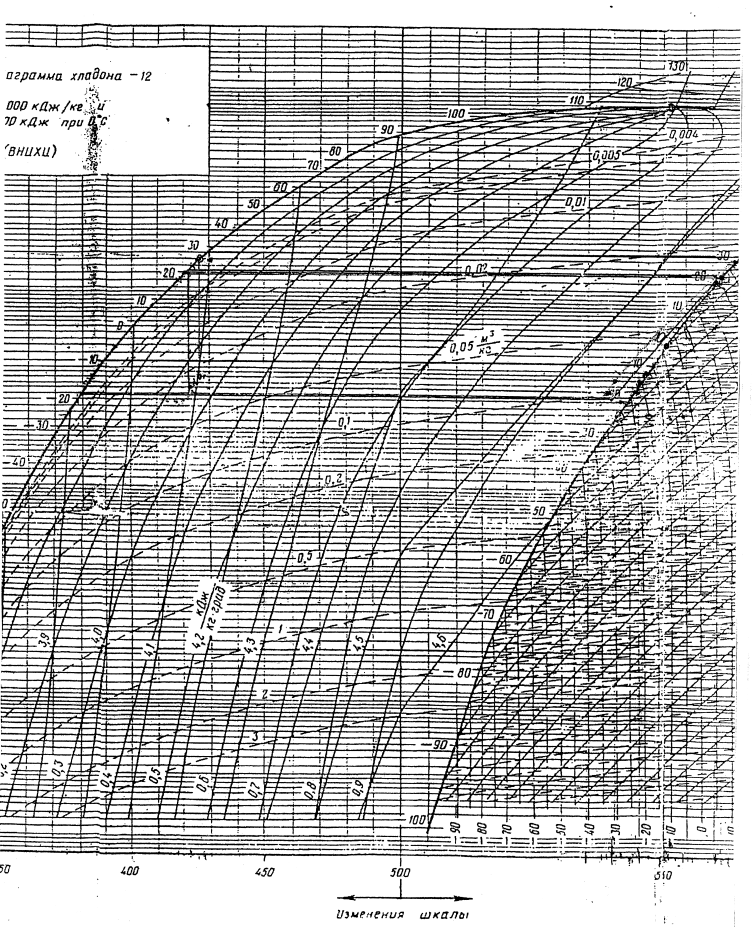
Рисунок 4.1 – диаграмма в ln р, h – координатах

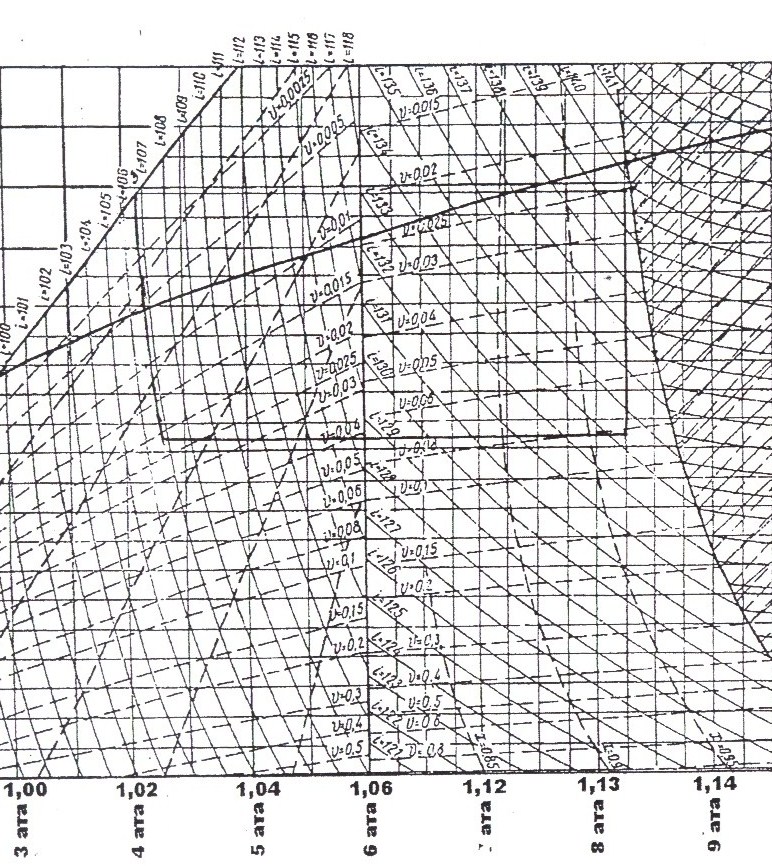
Рисунок 4.2– диаграмма в Т,S – координатах.

Заключение

В ходе этой работы я рассмотрел газовые процессы и циклы, паросиловые установки, а также циклы трансформаторного тепла. И выяснила, что в изотермическом процессе изменение внутренней энергии равно нулю 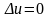и изменение энтальпии равно нулю 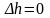; конечная энтропия получилась на много меньше начальной, потому что удельный объём в ходе процесса на много увеличился. Работа получается отрицательной, потому что в ходе процесса температура увеличилась. Энтропия и изменение энтропии в большей степени зависит от температуры, чем от объёма. С увеличением температуры, увеличивается и энтальпия, и внутренняя энергия.

Из анализа работы реального двигателя видно, что рабочий процесс не является замкнутым и в нём присутствуют все признаки необратимых процессов: трение, теплообмен при конечной разности температур, конечной скорости поршня и др.

Паросиловые установки отличаются от газотурбинных двигателей и двигателей внутреннего сгорания тем, что рабочим телом служит пар какой-либо жидкости (обычно водяной пар), а продукты сгорания топлива являются лишь промежуточным теплоносителем.

Библиографический список

1. Кириллин В. А., Сычев В. В., Шейндлинг А. Е. Техническая термодинамика: учебник для студентов вузов. – М.: МЭИ, 2008.

2. Баскаков А. П., Павлюк Е. Ю. Техническая термодинамика: учебное пособие – Екатеринбург: УралЮрИздат, 2010.

3. Захарова А. А. Техническая термодинамика и теплотехника: учебное пособие. – М.: Академия, 2006.

4. В.А. Кудинов. Техническая термодинамика. М.:Высшая школа.,2005.

81