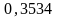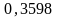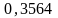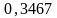- •Техническая термодинамика
- •Газовые процессы
- •1.1.1. Определение недостающих начальных параметров.
- •1.1.2. Определение недостающих конечных параметров.
- •1.1.3. Определение тепла, работы и изменения параметров внутренней энергии, энтальпии и энтропии.
- •1.2.1. Определение недостающих начальных параметров.
- •1.2.2. Определение недостающих конечных параметров.
- •1.2.3. Определение работы и изменения параметров: внутренней энергии, энтальпии и энтропии.
- •Газовые циклы.
- •2.1.1. Определение параметров газа в переходных точках цикла.
- •2.1.2. Определение тепла q, работы l и изменения параметров: внутренней энергии Δu, энтальпии Δh, энтропии Δs, в каждом процессе.
- •2.1.3. Определение полезной работы l, подведённого и отведённого тепла, кпд t (двумя способами).
- •2.2.1. Определение параметров газа в переходных точках цикла.
- •2.2.2. Определение тепла q, работы l и изменения параметров: внутренней энергии Δu, энтальпии Δh, энтропии Δs в каждом процессе.
- •2.2.3 Определение полезной работы l, кпд t (двумя способами).
- •3. Циклы паросиловых установок
- •3.1.6 Расчет термического кпд без промперегрева
- •4. Циклы трансформаторного тепла
- •4.1.1. Расчет удельной холодопроизводительности в цикле.
- •4.1.2. Расчет затраченной работы в цикле.
- •4.1.3. Расчет холодильного коэффициента в цикле.
3. Циклы паросиловых установок
3.1.Задача 1. В цикле паросиловой установки осуществляется одноступенчатый промежуточный перегрев пара до температуры t1. Определить термический КПД цикла при различных значениях давления промперегрева рп (2.0; 1.0; 0.5; 0.2; 0.1 МПа), построить зависимость t = f(рп), сравнить с термическим КПД без промперегрева. Построить цикл в T, s – и h, s – диаграммах.
Дано: "СИ"
р1
= 4,0 МПа
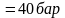
t1 = 420 оС
р2
= 14 кПа
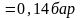
рп
= (2.0; 1.0; 0.5; 0.2; 0.1)МПа
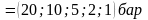
t - ?
График зависимости S(T) График зависимости S(h)
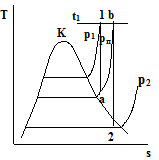
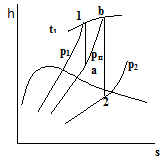
Решение:
Термический КПД цикла с промежуточным перегревом пара определяем по формуле:
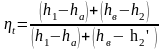 ,
(3.1)
,
(3.1)
где h1 – энтальпия в точке 1, кДж/кг;
hа – энтальпия в точке а, кДж/кг;
hв – энтальпия в точке в, кДж/кг;
h2 – энтальпия в точке 2, кДж/кг;
h2' = h3 = 4.19 t2 – энтальпия в точке 3, кДж/кг.
Рассчитаем термический КПД для каждого случая отдельно.
3.1.1 Расчет термического КПД при давлении промперегрева рп = 20 бар.
По h, s – диаграмме для водяного пара находим энтальпии:
h1 = 3261 кДж/кг,
hа = 3068 кДж/кг,
hв = 3292 кДж/кг,
h2 = 2344 кДж/кг,
h2' = 4.19 t2 = 4.19·55=230,45 кДж/кг.
Энтальпии h1 и h2' в каждом рассмотренном нами случае будут одинаковы.
Подставим значения энтальпий в формулу (3.1.1.):
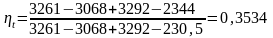
3.1.2 Расчет термического КПД при давлении промперегрева рп =10 бар
Аналогично находим энтальпии:
hа = 2897 кДж/кг,
hв = 3306 кДж/кг,
h2' = 2432 кДж/кг.
Подставим значения энтальпии в формулу (3.1.1.):
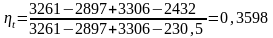
3.1.3 Расчет термического КПД при давлении промперегрева рп = 5 бар
Аналогично находим энтальпии:
hа = 2755 кДж/кг,
hв = 3314 кДж/кг,
h2' = 2540 кДж/кг.
Подставим значения энтальпии в формулу (3.1):
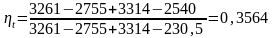
3.1.4 Расчет термического КПД при давлении промперегрева рп = 2 бар
Аналогично находим энтальпии:
hа = 2592 кДж/кг,
hв = 3318 кДж/кг,
h2' = 2684 кДж/кг.
Подставим значения энтальпий в формулу (3.1.1.):
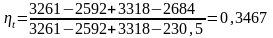
3.1.5 Расчет термического КПД при давлении промперегрева рп = 1 бар
Аналогично найдем энтальпии:
hа = 2484 кДж/кг,
hв = 3320 кДж/кг,
h2' = 2813кДж/кг.
Подставим значения энтальпий в формулу (3.1.1.):
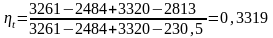
3.1.6 Расчет термического кпд без промперегрева
По h, s – диаграмме определим энтальпии:
h1 = 3261 кДж/кг,
h2 = 2210 кДж/кг,
t2 = 55оС.
Термический КПД без промперегрева рассчитаем по формуле:
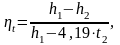 (3.2)
(3.2)
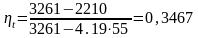 .
.
Найденные значения КПД приведены в табл. (3.1).
Таблица З.1 - Зависимости t = f(рп) и термического КПД без промперегрева
рп, бар |
20 |
10 |
5 |
2 |
1 |
без п. |
ηt |
|
|
|
|
|
|
3.1.7 Построение зависимости t = f(рп) и сравнение с термическим КПД без промперегрева.
График зависимости t = f(рп) показан на рисунке 3.1.
Вывод: из T,s - диаграммы видно, что промежуточный перегрев позволяет значительно увеличить сухость пара на выходе из турбины, это сказывается на благоприятные условия турбины.
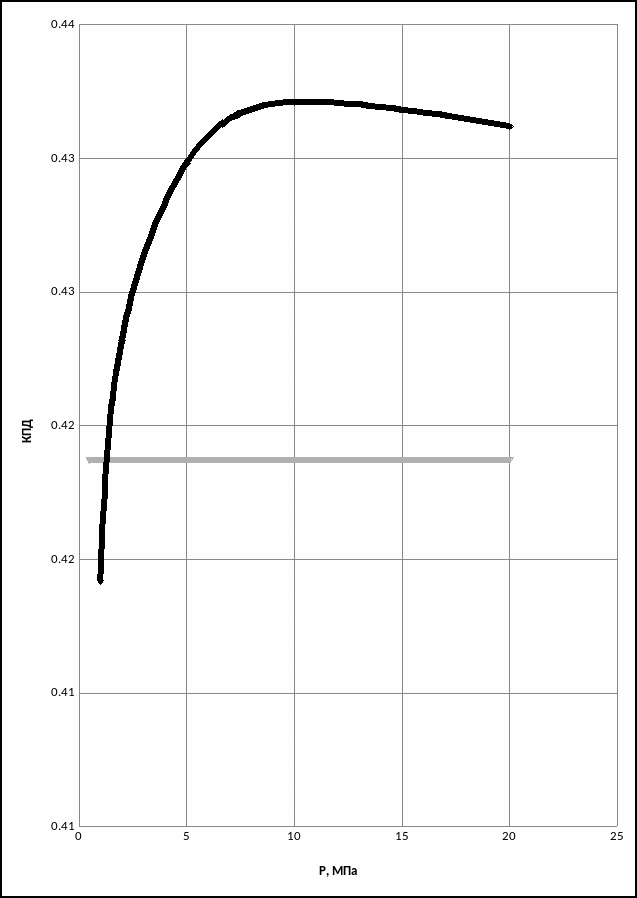
Рисунок 3.1 – график зависимости t = f(рп).
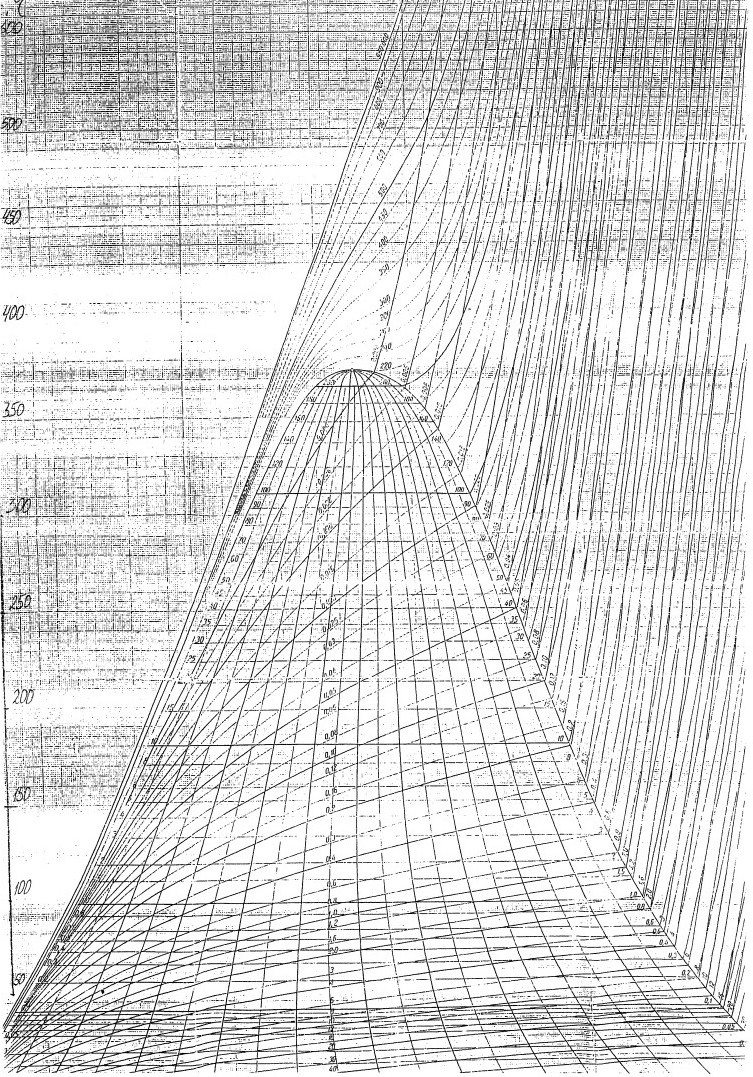
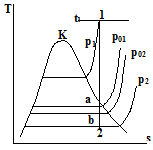
Рисунок 3.2 – диаграмма в Т,S – координатах.
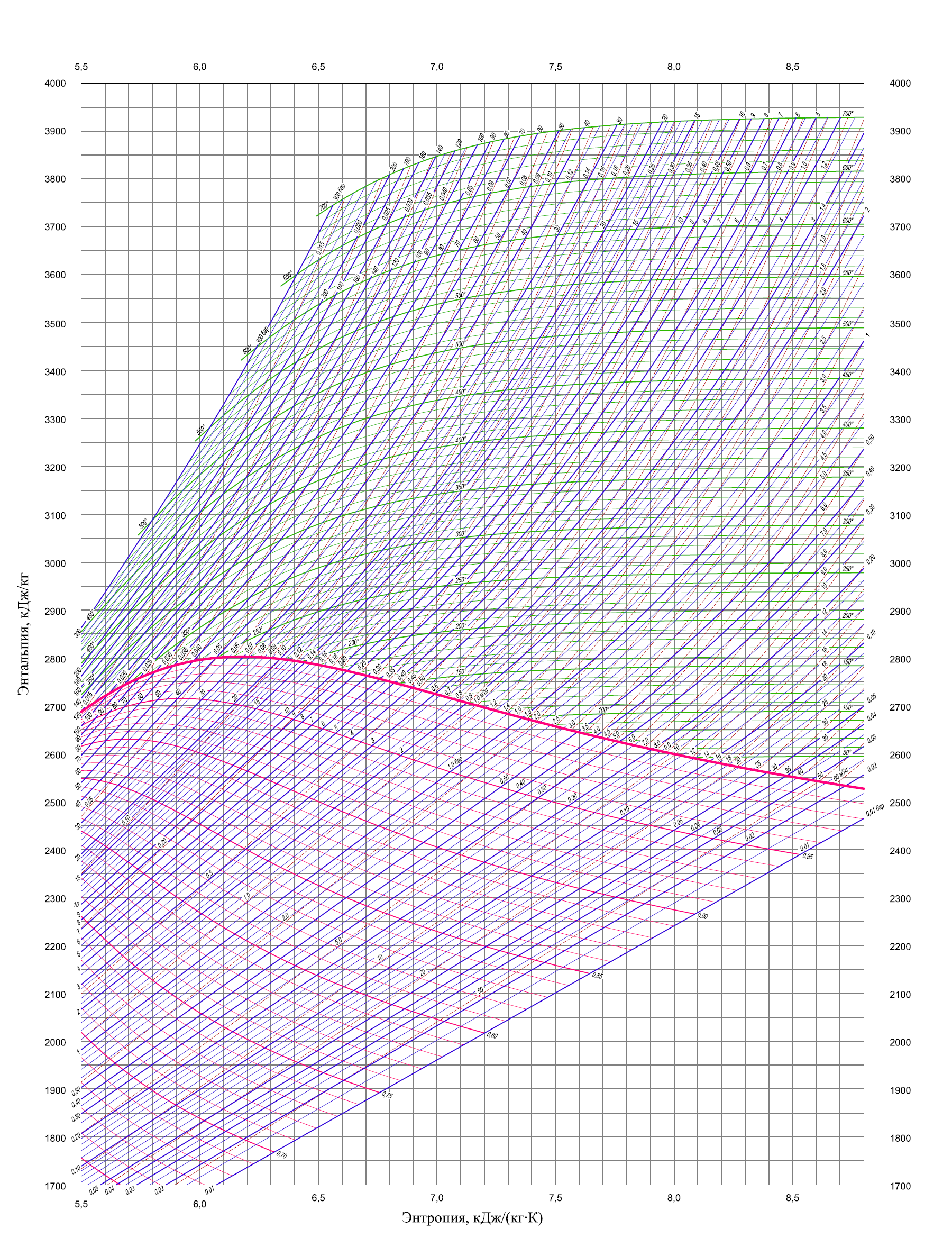
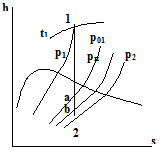
Рисунок 3.3 – диаграмма в h,S – координатах.
3.2. Задача 2. Паросиловая установка работает по циклу с двухступенчатым подогревом питательной воды в смесительных теплообменных аппаратах, давление первого отбора р01 = 0.6 МПа, второго отбора р02 = 0.12 МПа. Определить термический КПД регенеративного цикла, построить цикл в T, s – и h, s – диаграммах, сравнить с КПД обычного цикла Ренкина.
Дано: "СИ"
р01
= 0.3МПа
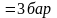
р02
= 0.12 МПа
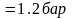
р1
= 8 МПа
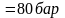
t1 = 470 оС
р2
= 9 кПа
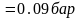
t - ?
График зависимости S(T) График зависимости S(h)
Решение:
Термический КПД регенеративного цикла рассчитаем по формулам:
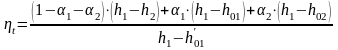 ,
(3.3)
,
(3.3)
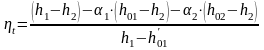 ,
(3.4)
,
(3.4)
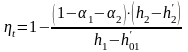 ,
(3.5)
,
(3.5)
где
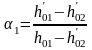 ,
(3.6)
,
(3.6)
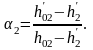 (3.7)
(3.7)
h1 – энтальпия в точке 1, кДж/кг;
h2 – энтальпия в точке 2, кДж/кг;
h01 – энтальпия в точке О1,кДж/кг;
h02 – энтальпия в точке О2, кДж/кг;
h'01 = 4,19 t01,
h'02 = 4,19 t02,
h'2 = 4,19 t2.
По h, s – диаграмме находим нужные для расчета энтальпии и температуры:
h1 = 3350 кДж/кг, t1 = 470 oC,
h2 = 2140 кДж/кг, t2 = 44 оС,
h01 = 2644 кДж/кг, t01 = 133 оС,
h02 = 2494 кДж/кг, t02 = 107 оС.
3.2.1 Рассчитаем энтальпии h'01, h'02, h'2
h'01
=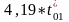 =
557,3кДж/кг,
=
557,3кДж/кг,
h'02
=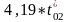 =
448,3 кДж/кг,
=
448,3 кДж/кг,
h'2
=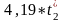 =
184,36 кДж/кг.
=
184,36 кДж/кг.
3.2.2 Рассчитаем 1 и 2
1 рассчитаем по формуле (3.2.4):
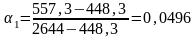 ,
,
2 рассчитаем по формуле (3.6):
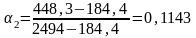 .
.
3.2.3 Расчет термического КПД регенеративного цикла
Рассчитаем термический КПД по формуле (3.2.1):
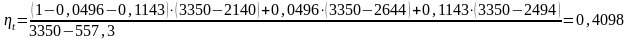 .
.
Теперь рассчитаем термический КПД по формуле (3.7):
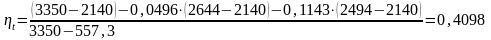 .
.
Рассчитаем термический КПД по формуле (3.2.3):
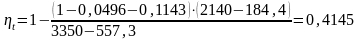 .
.
3.2.4 Расчет термического КПД обычного цикла Ренкина
Термический КПД цикла Ренкина рассчитаем по формуле:
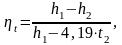 (3.8)
(3.8)
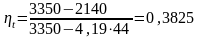 .
.
Вывод: цикл с регенеративным подогревом питательной воды имеет более высокий КПД по сравнению с циклом Ренкина. Введение регенерации может быть выгодным лишь до определенной температуры питательной воды, подогреваемой в регенераторах, превышение которой приводит к необходимости отбирать для этих целей из турбины пар более высоких параметров. В этом случае может возникнуть ситуация, когда уменьшение полезной работы на лопатках турбины окажется большим, чем уменьшение количества теплоты, затрачиваемой на выработку 1 кг пара, а удельный расход теплоты на единицу работы из – за увеличения удельного расхода пара будет возрастать. В связи с чем выгода, получаемая от применения регенерации, будет уменьшаться и при определенных условиях может оказаться равной нулю. Поэтому для каждой тепловой электрической станции существует определенная температура питательной воды, подогреваемой в регенераторах, которая дает максимальную прибавку КПД.
Рисунок 3.4 – диаграмма в Т,S – координатах.
Рисунок 3.5 – диаграмма в h,S – координатах