2.Модель с двумя независимыми переменными

Обобщением линейной регрессионной модели с двумя переменными является многомерная регрессионная модель (или модель множественной регрессии). Уравнение множественной регрессии может быть представлено в виде

где вектор независимых (объясняющих) переменных; вектор параметров (подлежащих определению); случайная ошибка (отклонение); зависимая (объясняемая) переменная.

Рассмотрим самую употребляемую и наиболее простую модель множественной регрессии – модель множественной линейной регрессии.

Теоретическое линейное уравнение регрессии имеет вид:

или для индивидуальных наблюдений

Здесь 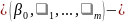вектор размерности неизвестных параметров. называется j-м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии). Он отражает влияние на условное математическое ожидание зависимой переменной объясняющей переменной 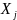при условии, что все другие объясняющие переменные модели остаются постоянными. свободный член, определяющий значение в случае, когда все объясняющие переменные равны нулю.

Если число наблюдений , то существует бесконечно много различных векторов параметров, при которых линейная формула (3) связи между X и Y будет выполняться абсолютно точно. Если число наблюдений , то вектор β рассчитывается единственным образом. При возникает необходимость оптимизации, т.е. оценивания параметров при которых формула (3) дает наилучшее приближение для имеющихся наблюдений.

В данном случае число называется числом степеней свободы.

Наиболее распространенным методом оценки параметров уравнения множественной регрессии является метод наименьших квадратов (МНК).

Требования мнк

1. Математическое ожидание случайного отклонения равно нулю для всех наблюдений:

2. Гомоскедастичность (постоянство дисперсии отклонений):

для любых наблюдений i и j.

3. Отсутствие автокорреляции.

Случайные отклонения и являются независимыми друг от друга для всех и .

4. Случайное отклонение должно быть независимо от объясняющих переменных.

5. Модель является линейной относительно параметров.

Для случая множественной линейной регрессии существенными являются еще два требования.

6. Отсутствие мультиколлинеарности.

Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.

7. Ошибки б имеют нормальное распределение .

Выполнение данного требования важно для проверки статистических гипотез и построения интервальных оценок.

Представим выражение (3) в матричной форме:

Здесь вектор-столбец значений зависимой переменной, Т – символ транспонирования, вектор-столбец (размерности m+1) неизвестных коэффициентов регрессии, вектор-столбец случайных отклонений, матрица размерности :

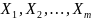В этой матрице -я строка представляет наблюдение вектора значений независимых переменных ; единица соответствует переменной при свободном члене .

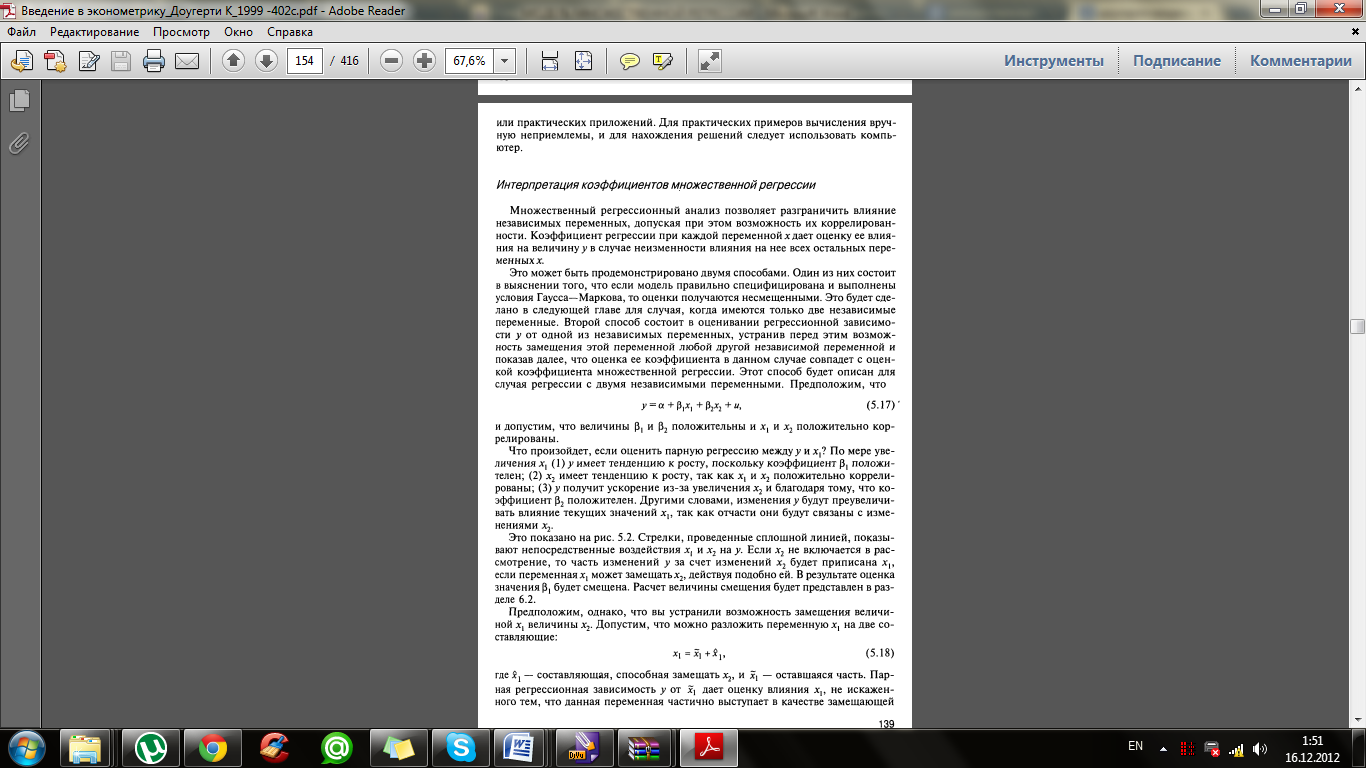
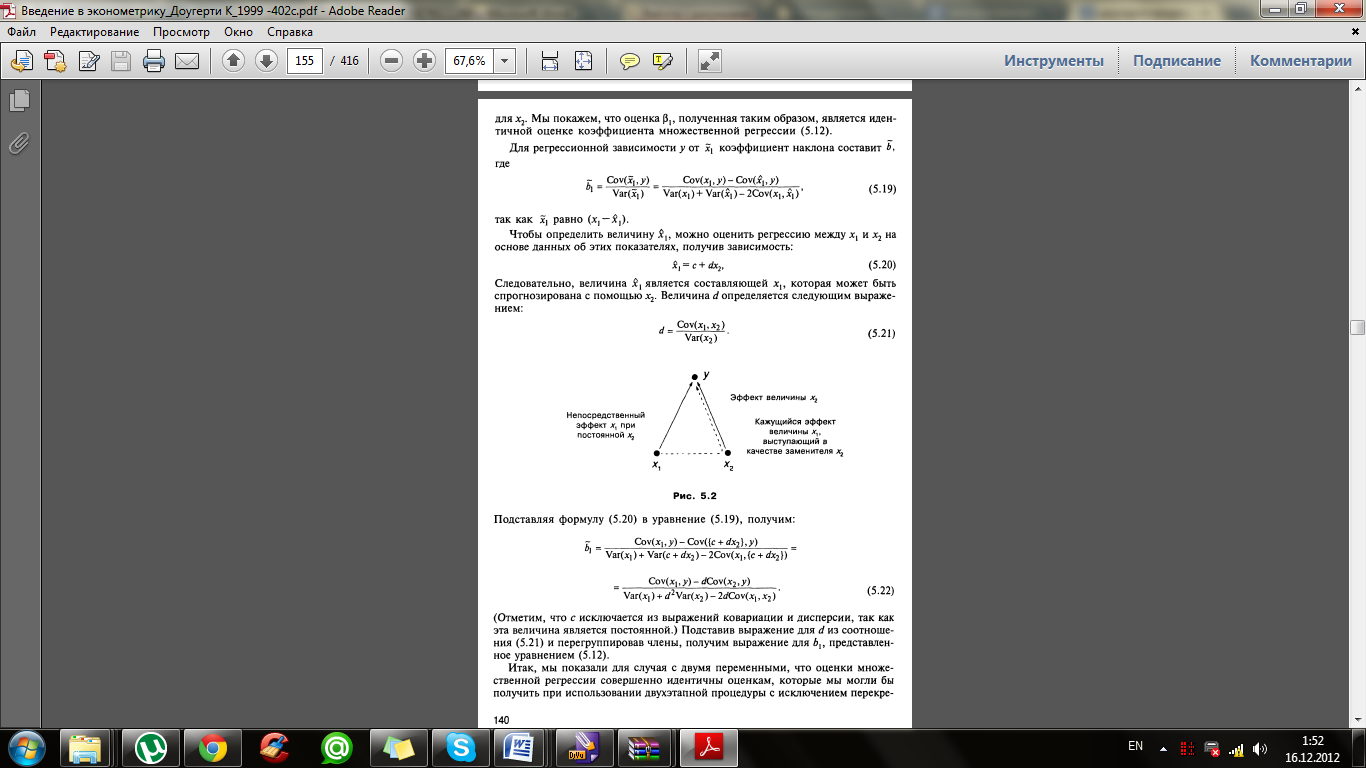
3.Вывод и интерпретация коэффициентов множественной регрессии

4.Множественная регрессия в нелинейных моделях