39.Основні труднощі розв’язання т-задач.

Практичне застосування класичної економіко-математичної моделі транспортної задачі наштовхується на певні труднощі.

1. Насамперед, як правило, необхідно перевозити неоднорідні продукти.

2. Часто господарські зв’язки між постачальниками і споживачами вимагають відповідних обмежень:

; ,

де М1, М2 — відповідні множини індексів i, j, за якими вводяться обмеження на обсяги перевезень і-ї продукції до j-го споживача. Обмеженнями   гарантується, що відповідний j-й споживач отримає і-ї продукції не менше від заданого обсягу. Обмеженнями виду   описують транспортні можливості.

3. У класичній транспортній задачі, як правило, критерієм оптимальності є мінімізація транспортних витрат, тобто розв’язується задача на мінімум. Проте на практиці бувають випадки, коли необхідно знайти максимум цільової функції. Наприклад, необхідно розподілити робітників (верстати) між окремими видами робіт, щоб отримати максимальну сумарну продуктивність праці. Подібна ситуація має місце за оптимізації розміщення сільськогосподарських культур на ділянках землі різної якості. У такому разі критерієм оптимальності є максимізація вартості вирощеної (валової) продукції.

4. У класичній транспортній задачі допускається, що витрати на транспортування лінійно залежать від обсягів перевезень. Але на практиці ця умова порушується, тобто такі зв’язки, як правило, є нелінійними, стохастичними тощо. Особливої уваги заслуговує така постановка транспортної задачі, в якій необхідно мінімізувати тривалість виконання заданих обсягів робіт, наприклад, перевезення сировини та продукції, яка швидко псується. Цей критерій часто використовується для оптимізації військових операцій, виконання сільськогосподарських робіт (наприклад, збору урожаю) тощо.

5. Транспортна задача значно ускладнюється за моделювання виробничо-транспортних економічних систем, які виробляють продукцію в широкому асортименті, а для перевезення її застосовують різні види транспорту.

40Постановка знп. Умовні та безумовні нелінійні задачі

Однак, загальновідомим є факт, що за умов ринкової конкурен­ції питання реалізації продукції є досить складним. Обсяг збуту продукції визначається передусім її ціною, отже, як цільову функ­цію доцільно брати максимізацію не всієї виготовленої, а лише реалізованої продукції. Необхідно визначати також і оптимальний рівень ціни на одиницю продукції, за якої обсяг збуту був би максимальним. Для цього її потрібно ввести в задачу як невідому величину, а обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція в такому разі буде виражена добутком двох невідомих величин: оптимальної ціни одиниці продукції на оптимальний обсяг відповідного виду продукції, тобто буде нелінійною. Отже, маємо задачу нелінійного програмування. Також добре відома транспортна задача стає нелінійною, якщо вартість перевезення одиниці товару залежить від загального обсягу перевезеного за маршрутом товару. Тобто коефіцієнти при невідомих у цільовій функції, що в лінійній моделі були сталими величинами, залежатимуть від значень невідомих (отже, самі стають невідомими), що знову приводить до нелінійності у функціоналі.

І нарешті, будь-яка задача стає нелінійною, якщо в математич­ній моделі необхідно враховувати умови невизначеності та ризик. Як показник ризику часто використовують дисперсію, тому для врахування обмеженості ризику потрібно вводити нелінійну функцію в систему обмежень, а мінімізація ризику певного процесу досягається дослідженням математичної моделі з нелінійною цільовою функцією.

Загальна задача математичного програмування формулюється так: знайти такі значення змінних x_j 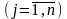, щоб цільова функція набувала екстремального (максимального чи мінімального) значення:

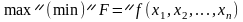за умов:

( ); .

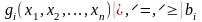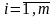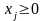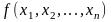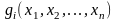Якщо хоча б одна з функцій та , є нелінійною маємо задачу нелінійного програмування.

У теорії дослідження функцій задача на відшукання екстремальних значень не містить ніяких додаткових умов щодо змінних і такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції

Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції.

Розділяють задачі безумовної та умовної оптимізації. Задачами безумовної оптимізації називаються задачі оптимізації функції багатьох змінних без додаткових обмежень. Завданнями умовної оптимізації називаються задачі про оптимізації цільової функції багатьох змінних f (x1, ..., xn) за умови, що ці змінні задовольняють наступним обмеженням: qi (x1, ..., xn) = 0, або dj (x1, ..., xn) 0,