Определение

Пусть   — выборка из распределения вероятности, определённая на некотором вероятностном пространстве  . Тогда её выборочным средним называется случайная величина

.

Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии.

Определения

Пусть   — выборка из распределения вероятности. Тогда

• Выборочная дисперсия — это случайная величина

,

где символ   обозначает выборочное среднее.

• Несмещённая (исправленная) дисперсия — это случайная величина

.

Исправленная дисперсия.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

  

  Для исправления выборочной дисперсии достаточно умножить ее на дробь

получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

11.6

СТАТИСТИЧЕСКАЯ ОЦЕНКА, функция от результатов наблюдений, применяемая для оценки неизвестных параметров распределения вероятностей изучаемых случайных величин.

Статистические оценки — это статистики, которые используются для оценивания неизвестных параметров распределений случайной величины.

Например, если   — это независимые случайные величины, с заданным нормальным распределением  , то   будет средним арифметическим результатов наблюдений.

Задача статистической оценки формулируется так:

Пусть   — выборка из генеральной совокупности с распределением  . Распределение   имеет известную функциональную форму, но зависит от неизвестного параметра  . Этот параметр может быть любой точкой заданного параметрического множества  . Используя статистическую информацию, содержащуюся в выборке  , сделать выводы о настоящем значении параметра  .

1 1.7

11.8

11.9

11.10

11.11

1 1.12

11.13.МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ МЕТОД

- метод оценивания неизвестных параметров для распределения случайной величины c по наблюдению её реализаций при параметрич. анализе данных.M. п. м. был предложен P. Э. Фишером (R. A. Fisher) в 1912 и формулируется след, образом. Пусть плотность вероятности величины х есть   где   - вектор неизвестных параметров. Определим ф-цию правдоподобия выражением 

к-рое в отличие от плотности вероятности   рассматривают как ф-цию вектора а при заданном векторе c реализовавшихся значений  . Оценкой M. п. м. паз. вектор   отвечающий максимуму выражения (1) и принадлежащий допустимой области значений   Часто ищут максимум выражения   что упрощает задачу поиска  для экспоненциальных распределений. Идея M. п. м. заключается в том, что данная реализация вектора   должна отвечать наиболее вероятному значению  , а потому при заданном   выражение   должно принимать макс, значение. Напр., время жизни г нестабильных частиц подчиняется распределению   где  - неизвестный параметр, характерный для каждой частицы. Пусть измерены времена жизни  для N распадов. Если пренебречь ошибками измерений   то ф-ция правдоподобия равна 

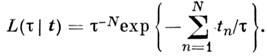
Оценка M. п. м. получается из решения ур-ния правдоподобия 

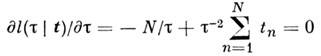
и равна 

С M. п. м. связано неравенство Крамера - Рао: дисперсия D (а )оценки параметра а, полученной любым методом, удовлетворяет неравенству 

где 

наз. смещением оценки 

наз. кол-вом информации в  о параметре а. В случае вектора параметров  неравенство (2) обобщается след, образом. Если ввести ср. значения 

ковариационную матрицу 

матрицу  и информац. матрицу 

то справедливо неравенство 

где I -единичная матрица, т означает транспонирование. Если оценки  являются несмещёнными, то для дисперсий  как это следует из (3), выполняется неравенство 

Неравенство Крамера - Рао полезно тем, что позволяет ещё на стадии планирования эксперимента оценить достижимую точность "измерения" параметров изучаемых распределений.

При нек-рых ограничениях на   можно показать, что оценка M. п. м. состоятельна, т. е. при   один из корней ур-ния правдоподобия,   стремится к точному значению а. Оценка M. п. м. асимптотически распределена по нормальному закону с нулевым ср. значением и дисперсией, равной  .

При конечных N оценка M. п. м., вообще говоря, является смещённой. Оптим. свойством оценки M. п. м. при конечных Nоказывается то, что при нек-рых условиях   достигает нижней границы, задаваемой неравенством Крамера - Рао (2). В общем случае свойства оценки M. п. м. можно изучить при помощи Монте-Карло метода: задавая значение a из области возможных значений, получают выборку   находят оценку  и строят её среднее значение и ковариационную матрицу. Другое оптимальное свойство оценки M. п. м.: оценка  ф-ции /(а) равна  . В этом её преимущества перед оценкой по наименьших квадратов методу.

11.14. Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своейпростоты и эффективности методов оценки параметров линейных эконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно “хорошо” отображать закономерности развития процесса  .

Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2):

y_t = a₀ + a₁ х_1t +...+ a_n х_nt + ε_t .

Исходными данными при оценке параметров a₀ , a₁ ,..., a_n является вектор значений зависимой переменной y = (y₁ , y₂ , ... , y_T )' и матрица значений независимых переменных

в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели  .

Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.

11.15       Интервальные оценки параметров распределения.

  Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок .

Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного пара­метра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d , то чем меньше d , тем оценка точнее.

  Таким образом, положительное число d характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.

  Надежностью (доверительной вероятностью) оценки называют вероятность g , с которой осуществляется неравенство |Q—Q* | <d .

Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что, |Q- Q*| <d равна g:

P(|Q- Q*| <d)= g.

Заменив неравенство равносильным ему двойным неравенством получим:

Р [Q* —d< Q < Q* +d] = g

  Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.

  Интервал (Q* - d Q* +d) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью g.

11.16.Доверительный интервал для математического ожидания нормально распределенной случайной величины с неизвестной дисперсией

В случае неизвестной дисперсии постановка задачи и ход рассуждений при построении доверительного интервала аналогичны случаю известной дисперсии, рассмотренному в предыдущем параграфе. Разница состоит в том, что в выражении (1) неизвестное среднеквадратичное отклонение   заменяется на его выборочную оценку s

Полученная таким путем статистика t, будучи довольно сложной функцией от нормально распределенных случайных величин х₁,х₂,...,x_n, уже не будет нормально распределенной. Можно доказать, что t имеет t -распределение Стьюдента с n-1 степенями свободы. Отсюда следует, что справедливо равенство

аналогичное уравнению (3) и отличающееся от него заменой   на s и квантилей нормального распределения на соответствующие квантили t -распределения с n-1 степенями свободы. Соответственно  -ный доверительный интервал для неизвестного математического ожидания   нормального распределения с неизвестной дисперсией   будет иметь следующий вид

Известно, что этот доверительный интервал и доверительный интервал из предыдущего раздела являются робастными, т.е. они нечувствительны к умеренным отклонениям от предположения о нормальности распределения. Во всяком случае, как отмечается в пособиях по математической статистике, при объеме выборки не менее 15 становится целесообразно использовать приведенные доверительные интервалы для математического ожидания и в случае умеренного отклонения от предположения о нормальности.

Заметим, что при   t-распределение приближается к нормальному распределению, а его квантили - к квантилям нормального распределения. Например, при n-1=60 квантиль   равна 2.00, что не очень сильно отличается от аналогичного значения   для нормального распределения (особенно на фоне выборочных флуктуаций   и s). Поэтому при числе наблюдений порядка нескольких десятков можно пользоваться нормальным приближением для t-распределения. Однако при небольшом числе степеней свободы различие между квантилями t-распределения и нормального распределения довольно значительно. Например, для n-1=1 имеем  , дляn-1=2 -  , для n-1=5 -  . При n-1=9 (выборка из 10 наблюдений) получаем значение  , что уже не очень сильно отличается от 1.96.

Возвращаясь к примеру с длинами лепестков ириса и учитывая, что  , s=0.47,   (при числе степеней свободы n-1=49), а также предполагая, что распределение длин лепестков нормально (в следующем разделе мы рассмотрим процедуру проверки этого предположения), получаем, что 95%-ным доверительным интервалом для математического ожидания длины лепестка будет интервал (4.13, 4.39). Т.е. мы можем утверждать, что с вероятностью 0.95 неизвестное   находится между 4.13 и 4.39 (точнее следует сказать, что найденный доверительный интервал с вероятностью 0.95 накроет неизвестное значение  ).

 

11.17.Доверительный интервал для неизвестной дисперсии нормально распределенной случайной величины (при неизвестном математическом ожидании)

Для нахождения доверительного интервала для неизвестной дисперсии нормально распределенной случайной величины рассмотрим статистику

Можно показать, что эта статистика имеет ²-распределение с п-1 степенями свободы. Следовательно, справедливо равенство

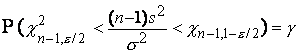
которое можно переписать в виде

Таким образом, 100%-ный доверительный интервал для неизвестной дисперсии   нормального распределения с неизвестным математическим ожиданием   будет иметь следующий вид

где   и   - квантили распределения ² с п -1 степенями свободы. В частности, для длины лепестков ириса, учитывая, что s² =0.22, n-1=49,   и  , получаем, что 95%-ным доверительным интервалом для дисперсии (в предположении нормальности распределения) будет интервал (0.15, 0.34).

Заметим, что полученный доверительный интервал для дисперсии, в отличии от доверительного интервала для математического ожидания, чувствителен к отклонениям от исходного предположения о нормальности распределения.

11.18. Доверительный интервал для среднего квадратичного отклонения

Пусть количественный признак Х генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратичное отклонение   по исправленному среднему квадратичному отклонению  . Для этого найдем доверительный интервал, покрывающий неизвестный параметр   с надежностью  . В сущности, задача повторяет предыдущий раздел, но сейчас мы немного изменим обозначения для упрощения записи результата. Выражение для доверительной вероятности имеет вид  , где   – абсолютная погрешность оценивания. Неравенство   или равносильное ему неравенство   преобразуем к виду  . Обозначим   и, поскольку абсолютную погрешность оценивания мы выбираем достаточно малой, можно считать, что  . Перепишем неравенство в виде  , домножим на  , получим  . Из предыдущего раздела известно, что случайная величина   имеет распределение Пирсона   с   степенями свободы. Поэтому переменную   можно выразить через значения критических точек   и   распределения Пирсона и записать эти значения в таблицу (в приложении значения параметра   приведены в табл. 3). Вычислив по выборке значение   и найдя по таблице  , получим искомый доверительный интервал для среднего квадратичного отклонения, покрывающий параметр   с заданной надежностью  :  .

Замечание. В случаях, когда оценивается математическое ожидание при неизвестной дисперсии или дисперсия при неизвестном математическом ожидании, получающиеся при этом доверительные интервалы оказываются длиннее тех, что получены, когда, соответственно, дисперсия или математическое ожидание были известны. Это обстоятельство объясняется тем, что наличие дополнительной информации позволяет сузить пределы, в которые можно заключить оцениваемый параметр при заданной надежности.

11.19 общие положения по задаче статистической поверки гипотез

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки [3, 5, 11]. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.

Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н₀. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н₁. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.

Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н₀ о равенстве l =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н₀ о неравенстве l >10 состоит из бесконечного множества простых гипотез Н₀ о равенстве l =b_i , где b_i – любое число, большее 10. Гипотеза Н₀ о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x₁, x₂, …, x_n). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S₀ и S₁. Если значение критерия z попадает в область S₀, то гипотеза принимается, а если в область S₁, – гипотеза отклоняется. Множество S₀ называется областью принятия гипотезы или областью допустимых значений, а множество S₁ – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.

Принятие или отклонение гипотезы Н₀ по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью a тогда, когда отвергается верная гипотеза Н₀ и принимается конкурирующая гипотеза Н₁. Ошибка второго рода возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н₀, в то время как справедлива конкурирующая гипотеза Н₁.Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н₀. Вероятность отвергнуть ложную гипотезуН₀ называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре вариант а исходов, табл:

Гипотеза Н0	Решение	Вероятность	Примечание
Верна	Принимается	1–a	Доверительная вероятность
	Отвергается	a	Вероятность ошибки первого рода
Неверна	Принимается	b	Вероятность ошибки второго рода
	Отвергается	1–b	Мощность критерия

Например, рассмотрим случай, когда некоторая несмещенная оценка параметра q вычислена по выборке объема n, и эта оценка имеет плотность распределения f(q ), рис. 3.1.

Рис. 3.1. Области и отклонения гипотезы

Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н₀ о равенстве q =Т, то насколько велико должно быть различие между q и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между q и Т на основе выборочного распределения параметра q .

Целесообразно полагать одинаковыми значения вероятности выхода параметра q за нижний и верхний пределы интервала. Такое допущение во многих случаях позволяет минимизировать доверительный интервал, т.е. повысить мощность критерия проверки. Суммарная вероятность того, что параметр q выйдет за пределы интервала с границами q _1–a /2 и q a _/2, составляет величину a . Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства q =Т можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания отвергнуть гипотезу Н₀. Отсюда следует, что вероятность допустить ошибку первого рода равна a (равна уровню значимости критерия).

Если предположить, например, что истинное значение параметра в действительности равно Т+d, то согласно гипотезе Н₀ о равенстве q =Т – вероятность того, что оценка параметра q попадет в область принятия гипотезы, составит b , рис:

При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a . Однако при этом увеличивается вероятность ошибки второго рода b (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т – d.

Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность a была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения a относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами q _1–a /2 и q a_/2 для типовых значений a и различных способов построения критерия.

При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия.

В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента.

11.20 критерий пирсона в проверке гипотез о законе распределения

Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределениемF_п(x), которая приближенно подчиняется закону распределения c ². Гипотеза Н₀ о согласованности распределений проверяется путем анализа распределения этой статистики. Применение критерия требует построения статистического ряда.

Итак, пусть выборка представлена статистическим рядом с количеством разрядов y . Наблюдаемая частота попаданий в i-й разряд n_i. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет F_i. Разность между наблюдаемой и ожидаемой частотой составит величину (n _i – F_i). Для нахождения общей степени расхождения между F(x) и F_п(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда

.

Величина c ² при неограниченном увеличении n имеет распределение хи-квадрат (асимптотически распределена как хи-квадрат). Это распределение зависит от числа степеней свободы k, т.е. количества независимых значений слагаемых в выражении (3.7). Число степеней свободы равно числу y минус число линейных связей, наложенных на выборку. Одна связь существует в силу того, что любая частота может быть вычислена по совокупности частот в оставшихся y – 1 разрядах. Кроме того, если параметры распределения неизвестны заранее, то имеется еще одно ограничение, обусловленное подгонкой распределения к выборке. Если по выборке определяются f параметров распределения, то число степеней свободы составит k=y – _f –1.

Область принятия гипотезы Н₀ определяется условием c ^2£ c 2(k;a ), где c ²(k;a ) – критическая точка распределения хи-квадрат с уровнем значимости a . Вероятность ошибки первого рода равна a , вероятность ошибки второго рода четко определить нельзя, потому что существует бесконечно большое множество различных способов несовпадения распределений. Мощность критерия зависит от количества разрядов и объема выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).

11.21 критерий колмогорова в проверке в проверке гипотез о законе распределения

Для применения критерия А.Н. Колмогорова ЭД требуется представить в виде вариационного ряда (ЭД недопустимо объединять в разряды). В качестве меры расхождения между теоретической F(x) и эмпирической F_n(x) функциями распределения непрерывной случайной величины Х используется модуль максимальной разности

dn = max|F(x) - F_n(x)|.

А.Н. Колмогоров доказал, что какова бы ни была функция распределения F(x) величины Х при неограниченном увеличении количества наблюдений nфункция распределения случайной величины d_n  асимптотически приближается к функции распределения  . Иначе говоря, критерий А.Н. Колмогорова характеризует вероятность того, что величина d_n  не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия  , в силу предположения, что почти невозможно получить это равенство, когда существует соответствие между функциями F(x) и F_n(x). Критерий А.Н. Колмогорова позволяет проверить согласованность распределений по малым выборкам, он проще критерия хи-квадрат, поэтому его часто применяют на практике. Но требуется учитывать два обстоятельства.

Во-первых, в точном соответствии с условиями его применения необходимо пользоваться следующим соотношением

где  .

Во-вторых, условия применения критерия предусматривают, что теоретическая функция распределения известна полностью (известны вид функции и ее параметры). Но на практике параметры обычно неизвестны и оцениваются по ЭД. Это приводит к завышению значения вероятности соблюдения нулевой гипотезы, т.е. повышается риск принять в качестве правдоподобной гипотезу, которая плохо согласуется с ЭД (повышается вероятность совершить ошибку второго рода). В качестве меры противодействия такому выводу следует увеличить уровень значимости a , приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.