Метод канонических разложений

-- каноническое разложение случайного процесса; --случайный коэффициент с параметрами (некоррелированные); -- система координатных функций.

Корреляционная функция .

Дискретные реализации [n] непосредственно вычисляются по формуле.

В качестве используются выборочные значения некоррелированных случайных величин с параметром . Бесконечный ряд заменяется усеченным конечным.

Как выбрать систему координат функций и найти дисперсии ? Часто в качестве выбирают систему ортонормированных функций .

При этом дисперсии – собственные значения, --собственные функции интегрального уравнения .

Практически, нет простого способа решения таких уравнений. Существует приближенные способы получения канонических разложений.

Способ канонических разложений случайных функций в дискретном ряде.

Пусть задан случайный процесс (t) с корреляционной функцией ; последовательность точек .Аппроксимировать случайный процесс (t) случайным процессом *(t), представленным в виде канонического разложения, таким что, Позволяет получить каноническое разложение с помощью обычных алгебраических операций. Пусть требуется формировать значения (t) только в заданных N точках, вектор с корреляционной матрицей

 Метод разложения в ряд Фурье

Для стационарных случайных процессов наиболее простой частный случай ортогонального разложения на конечном интервале (0,T) – разложение в ряд Фурье. -- случайные амплитуды. При реализации случайного процесса является периодическими функциями с периодом .--нужно выбрать. --дисперсии коэффициентов .

10.11 Особое место среди случайных процессов занимают так называемые марковские случайные процессы, впервые описанные А.А. Марковым в 1907г. Случайный процесс называется марковским, если вероятность любого его состояния в будущем зависит только от состояния в настоящем и не зависит от того, каким образом и когда процесс пришел в текущее состояние. Аналитически сказанное может быть записано в виде:

Pr{g(t_n+1)=E_n+1|g(t₀)=E₀, g(t₁)=E₁, …, g(t_n)=E_n}=

=Pr{g(t_n+1)=E_n+1|g(t_n)=E_n},

где t₁<t₂< … <t_n<t_n+1, а E_n - текущее состояние. Иными словами, в марковских случайных процессах влияние (воздействие) всей предыстории процесса на его будущее полностью сосредоточено в текущем состоянии процесса. Это свойство называется свойством отсутствия последействия или применительно к случайным процессам марковским свойством.

Свойство отсутствия последействия накладывает существенные ограничения на распределение времени пребывания марковского процесса в том или ином состоянии. Так, в случае цепи Маркова с непрерывным временем время пребывания в данном состоянии должно быть распределено по экспоненциальному, а в случае дискретной цепи Маркова - по геометрическому, законам распределения, которые являются единственными, соответственно, непрерывным и дискретным распределениями без последействия. Только при таких ограничениях на времена пребывания процесса в состояниях гарантировано выполнение марковского свойства.

(2)

Рассмотрим марковский случайный процесс g(t) с конечным числом состояний E₀, E₁, …, E_n. Обозначим через P_i(t) вероятность того, что случайный процесс в момент времени t находится в состоянии E_i:

P_i = Pr{g{t} = E_i}, i = 0,n.

Очевидно, что в любой момент времени t процесс находится в одном из n+1 возможных состояний, т.е. события g{t}=E_i, i = 0,n заключающиеся в том, что в момент времени t процесс находится в состояниях E₀, E₁ ,…, E_n, образуют полную группу несовместных событий. Отсюда следует, что в любой момент времени t выполняется условие:

(3)

1, которое называется нормировочным. Совокупность вероятностей P_i(t), i=0,n, может быть представлена вектором, называемым вектором состояний, с числом компонент, равным числу возможных состояний процесса:

P(t)={P₀(t), P₁(t), …, P_n(t)}.

Главная задача изучения марковских случайных процессов заключается в определении вероятностей P_i(t), i = 0,n, нахождения процесса в любой момент времени t в том или ином состоянии, что дает полную информацию о случайном процессе. Для решения данной задачи необходимо:

1) указать в каком состоянии находится процесс в начальный момент времени;

2) описать переходы между состояниями.

Состояние процесса в начальный момент времени t=0 задается вектором начальных вероятностей

P(0)={P₀(0), P₁(0), …, P_n(0)}.

Описание переходов между состояниями зависит от того, каким (с дискретным или с непрерывным временем) является изучаемый марковский случайный процесс. Этот вопрос будет рассматриваться в следующих параграфах.

Очень часто при изучении марковских случайных процессов достаточно определить не вероятности P₀(t), P₁(t), …, P_n(t) в любой момент времени t, а их предельные значения (если они существуют) при .

Если при вероятности P_i(t), i=0,n, стремятся к предельным значениям P_i , i=0,n, не зависящим от распределения начальных вероятностей  P_i(0), i=0,n, то говорят, что случайный процесс обладает эргодическим свойством. Таким образом, для процессов, обладающих эргодическим свойством, существуют пределы

, i=0,n.

Предельные вероятности P_i, i=0,n, часто называют вероятностями состояний равновесия или стационарными вероятностями.

10.12 Це́пь Ма́ркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова (старшего).

Последовательность дискретных случайных величин называется простой цепью Маркова (с дискретным временем), если

.

Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний (в отличие от цепей Маркова высших порядков).

Область значений случайных величин называется простра́нством состоя́ний цепи, а номер  — номером шага.

Переходная матрица и однородные цепи

Матрица , где

называется ма́трицей перехо́дных вероя́тностей на -м шаге, а вектор , где

— нача́льным распределе́нием цепи Маркова.

Очевидно, матрица переходных вероятностей является стохастической, то есть

.

Цепь Маркова называется одноро́дной, если матрица переходных вероятностей не зависит от номера шага, то есть

.

В противном случае цепь Маркова называется неоднородной. В дальнейшем будем предполагать, что имеем дело с однородными цепями Маркова.

10.13 Распределение вероятностей  в произвольной момент времени  можно найти, воспользовавшись формулой полной вероятности

 (7)

Может оказаться, что  не зависит от времени. Назовем стационарным распределением вектор , удовлетворяющий условиям

,

     (8)

где вероятности перехода.

Если в цепи Маркова  то при любом

 

Это утверждение следует по индукции из (7) и (8).

Приведем формулировку теоремы о предельных вероятностях для одного важного класса цепей Маркова.

Теорема 1. Если при некотором >0 все элементы матрица  положительны, то для любых , при

, (9)

 

где  стационарное распределение с      а некоторая постоянная, удовлетворяющая неравенством 0<h<1.

Так как  , то по условию теоремы из любого состояния можно попасть в любое за время  с положительной вероятностью. Условия теоремы исключает цепи, являющиеся в некотором смысле периодическими.

Если выполнить условие теоремы 1, то вероятность того, что система находится в некотором состоянии , в пределе не зависит от начального распределение. Действительно, из (9) и (7) следует, что при любом начальном распределении  ,

 

11.1  Генеральная и выборочная совокупности.

Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений,  проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.

Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки.

 Выборочной совокупностью называют часть отобранных объектов из генеральной совокупности

11.2 Репрезентативная выборка – выборка людей из генеральной совокупности, позволяющая с высокой степенью достоверности ~4-5% переносить данные репрезентативной выборки на генеральную совокупность. Характеризуется таким же как и генеральная совокупность процентным составом основных социологических характеристик

Пусть мы делаем выборку поочередно m элементов (например, шаров) из n элементов. Мы можем возвращать очередной шар (в число n шаров), тогда при каждом очередном выборе мы будем иметь все те же n шаров. Такая выборка называется выборкой с возвращением. А можем и не возвращать шар, тогда при каждом выборе мы будем выбирать из все меньшего числа шаров. Такая выборка называется выборкой без возвращения.

11.4 Эмпирической функцией распределения   называется функция  , вычисляемая по выборке   следующим образом:

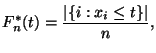
то есть,   есть отношение числа элементов выборки, не превосходящих  , к объему выборки.

Замечание 1  

Слово ``эмпирическая'' в Определении  означает, что функция вычисляется по данным опыта (эмпирическим данным), то есть, по выборке. По этой же причине для этого понятия иногда употребляют термин выборочная функция распределения.

Замечание 2  

Легко видеть, что   есть кусочно постоянная неубывающая непрерывная справа функция. Если все   различны, то в каждой точке   функция имеет скачок величины  . Если какие-либо из   совпадают, то соответствующие скачки суммируются.

Замечание 3  

Как следует из Определения значение функции   в точке   зависит от выборки , так что более полное обозначение для   могло быть следующим: . В этом обозначении переменная   является основной, а   -- фиксированные параметры. С другой стороны,   интерпретируются как реализации независимых одинаково распределенных случайных величин с функцией распределения  . Таким образом,   есть случайная величина.

Оказывается, что в пределе   выборочная функция распределения  равномерно сходится к теоретической:

(28)

Этот факт имеет совершенно общий характер и называется теоремой Гливенко

11.5

Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.