Определение случайных процессов.

Если некоторая физическая величина меняется со временем, то в таком изменении практически всегда есть случайная составляющая. В одних процессах эта составляющая пренебрежимо мала, и такие процессы называют детерминированными. В других эта составляющая заметна и часто представляет всю суть процесса.

Основной смысл случайного процесса   (случайной функции) заключается в том, что в каждый момент  значение функции  является случайной величиной. Однако задание распределений для каждого момента времени недостаточно для полного определения случайного процесса.

Пусть случайный процесс задан (исследуется) на отрезке времен  , и требуется дать такое определение этого процесса, чтобы оно охватывало всевозможные свойства процесса. С этой целью введем понятие дискретной выборки процесса, являющейся набором значений функции   для некоторой последовательности времен:

Сочетание выборок   есть  -мерная случайная величина.

Будем говорить, что процесс определен полностью, если для любой выборки (44) при любых   можно задать распределение   такое, что

есть вероятность того, что случайные величины   лежат в пределах

(предполагается, что   достаточно малы).

Причем эти распределения должны обладать следующими свойствами

Ясно, что не для всякого случайного процесса можно задать (или указать метод нахождения) распределение любой выборки. Редким исключением, в котором это можно сделать, является параметрический случайный процесс, когда   задается детерминированной функцией  , зависящей от случайного параметра  . Достаточно задать распределение   параметра  , и для   любой выборки имеем

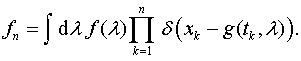
Возникает вопрос: как исследовать процессы, которые нельзя задать в полном объеме? Ответ лежит в практической плоскости. Во-первых, отрезок времени   на практике ограничен, а разности   не могут быть сколь угодно малыми, так как всякое измерение "расплывается" во времени. Т.е. число   не может быть сколь угодно большим. Во-вторых, основной объем информации о статистических свойствах процесса представляют распределения низших порядков. Очень часто достаточно знать   и  .

Если рассматриваются совместно несколько случайных процессов, то задается распределение соответствующего числа выборок. Например, для двух процессов   и   (45) обобщается в виде

причем наборы   и   могут принадлежать разным отрезкам времен.

Условные распределения определяются так же, как в (21, 22). Например,

есть вероятность того, что   при условии, что  . Для непрерывных процессов имеет место предел

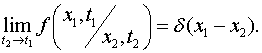
При рассмотрении двух процессов аналогом (48) будет

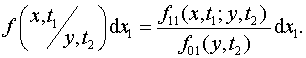
Определение средних значений по вероятностям отличается от (27-30) лишь тем, что индекс " " заменяется непрерывной величиной  ; т.е. результаты являются функциями времен:

Если существует предел

то процесс называют непрерывным в среднеквадратичном смысле. Иногда используют нормированные функции .

При совместном рассмотрении нескольких процессов к характеристикам (51), относящимся к отдельным процессам, добавляются смешанные средние. Для двух процессов   и   определяется взаимная корреляционная функция

При этом функции  , данные в (51), называют автокорреляционными. Далее мы будем говорить только о функции   (и называть ее просто корреляционной), подразумевая, что все операции с ней имеют смысл и для взаимной корреляционной функции.

10.8 Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что принимаемые ею значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x_k(t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 17.1.1. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

10.9 Пусть задан стационарный эргодический процесс s(t) со спектром W_вх ( ) и корреляционной функцией R_s,вх(). Требуется найти аналогичные характеристики для производной и интеграла от функции s(t). При дифференцировани ограничимся требованием: энергетический спектр W_вх ( ) при  должен убывать быстрее, чем    , т.е. 

Это условие выполняется для большинства практических задач (кроме белого шума с неограниченной полосой).

При дифференцировании передаточная функция цепи имеет вид

Следовательно,

Дисперсия случайного процесса на выходе

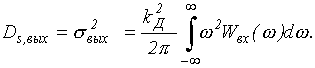
При интегрировании частотная характеристика цепи имеет вид

Тогда

Условием интегрируемости случайного процесса является неравенство

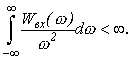
Это условие требует убывания функции W_вх ( ) быстрее чем при .

Идеальное интегрирующее устройство можно рассматривать как фильтр с бесконечно малой полосой пропускания (или бесконечно длинной импульсной характеристикой).Поэтому процесс установления длится бесконечно долго. В связи с этим статистические характеристики выходного сигнала зависят от времени интегрирования.

10.10