Дискретное совместное распределение.

Определение 35. Говорят, что случайные величины  ,   имеют дискретное совместное распределение, если существует конечный или счётный набор чисел   такой, что

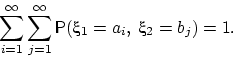
Таблицу, на пересечении  -й строки и  -го столбца которой стоит вероятность  , называют таблицей совместного распределения случайных величин   и  .

Таблицы распределения каждой из случайных величин  ,   в отдельности (таблицы частных, или маргинальных распределений) восстанавливаются по таблице совместного распределения с помощью формул:

Так, первое равенство следует из того, что набор  ,  , ...   есть полная группа событий, и поэтому событие   раскладывается в объединение попарно несовместных событий:

7 .6. Специфические свойства распределения дискретной многомерной случайной величины.

7.7 Основной способ описания непрерывной многомерной случайной величины.

7.8. специфические свойства функции распределения непрерывной многомерной случайной величины.

7.10 Определение независимости случайных величин

Понятие «независимости» случайных величин, которым мы пользуемся в теории вероятностей, несколько отличается от обычного понятия «зависимости» величин, которым мы оперируем в математике. Действительно, обычно под «зависимостью» величин подразумевают только один тип зависимости - полную, жесткую, так называемую - функциональную зависимость. Две величины   и   называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.

Определим понятие независимости для случайных величин.

Определение 2.6   Случайные величины   называются независимыми, если для всех 

Другими словами,   набор   есть набор независимых событий.

Упражнение 2.8   Показать, что события   независимы тогда и только тогда, когда случайные величины   взаимно независимы.

7.11 Понятие о независимых случайных величинах – одно их важных понятий теории вероятностей.

Случайная величина   называется независимой от случайной величины  , если закон распределения величины   не зависит от того, какое значение приняла величина  .

Для непрерывных случайных величин условие независимости   от   может быть записано в виде:

при любом  .

Напротив, в случае, если   зависит от  , то

.

Докажем, что зависимость или независимость случайных величин всегда взаимны: если величина   не зависит от  .

Действительно, пусть   не зависит от  :

.                                                            (8.5.1)

Из формул (8.4.4) и (8.4.5) имеем:

,

откуда, принимая во внимание (8.5.1), получим:

что и требовалось доказать.

Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.

Случайные величины   и   называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины   и   называются зависимыми.

Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:

,                                                              (8.5.2)

т. е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.

Условие (8.5.2) может рассматриваться как необходимое и достаточное условие независимости случайных величин.

Часто по самому виду функции   можно заключить, что случайные величины  ,   являются независимыми, а именно, если плотность распределения   распадается на произведение двух функций, из которых одна зависит только от  , другая - только от  , то случайные величины независимы.

7.15

Н екоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и ее направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.

7.16

.

7.17

7.18.

7.19.

Корреляционная зависимость между случайными величинами Х и У называется линейной корреляцией, если обе функции регрессии f(y) и g(x) являются линейными. В этом случае линии регрессии- прямые и называются прямыми регрессии.

Выведем уравнение прямой регрессии У на Х, т.е. найдем коэффициенты линейной функции g(x) = AX +B.

Введем обозначения М(Х) =а, М(У) =b, D(X) =s12, D(Y) ==s22, М(ХУ) – М(Х)М(У) = m .

Используем свойства математического ожидания:

М(У) =М(g(x))= M(AX +B) = AM(X) +B, тогда B = b – Aa.

M(XY) = M(Xg(x)) = M(AX 2 + BX ) = AM(X2) + BM(X) AM(X2) + (b – Aa)a, откуда

- называется коэффициентом регрессии У на Х. Уравнение прямой регрессии У на Х имеет вид :

7.20

7.21 Теорема о нормальной корреляции

Если двумерная случайная величина (X, Y) распределена по нормальному закону, то случайные величины X и Y связанны линейной корреляционной зависимостью.

8.1 Что значит «функция случайных величин»?

На самом деле функция случайных величин представляет операцию над случайными величинами.

Выявляются закономерности для различных операций над случайными величинами.

Для примера λ=λ (Σ, γ) – случайная величина, определяемая через сл. величины Σ, γ некой операцией (формулой). Тогда для закона распределения Fx (t), когда определяется неравенством Х (Σ, γ)<t в терминах данных Σ и γ.

Эти неравенства могут быть тяжелыми даже при простых операциях λ.

8.2 Определение функции распределения для функции случайных величин, зная законы распределения последних.

Функцией распределения случайных величин Х называется функция F(x), которая для любого числа x € R равна вероятности события {X < x}.

Таким образом по определению,

Функцию F(x) называют также интегральной функцией распределения.

Геометрически равенство можно истолковать так: F(x) есть вероятность того, что случайная величина Х примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е. случайная точка Х попадает в интервал (-∞, х)

8.3 Определение математического ожидания и дисперсии для варианта линейной функции нескольких случайных величин, зная характеристики последних.

Математическим ожиданием (или средним значением) дискретной случайной величины Х, имеющей закон распределения , называется число, равное сумме произведений всех ее значений на соответствующие им вероятности.

Математическое ожидание обозначается через МХ ( или: М[X], М(Х), ЕХ и т.д.)

Таким образом, по определению:

Если число возможных значений случайных величин бесконечно, то

Эти две формулы можно записать в виде:

Свойства математического ожидания:

1. математическое ожидание постоянной равно самой этой постоянной, т.е

Мс=с

2. Постоянный множитель выносится за знак математического ожидания, т.е.

М(сХ)=сМХ

3. Математическое ожидание суммы случайной величины равно сумме их математического ожидания, т.е.

М(Х+Y)=MX+MY

4. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю, т.е.

M(X-MX)=0

5. Математическое ожидание произведения независимых случайных величин равно произведению их математического ожидания, т.е. если Х и Y независимы, то

M(X*Y)=MX*MY

Дисперсией (рассеянием) случайной величины Х называется математическое ожидание квадрата ее отклонения от своего математического ожидания. Обозначается дисперсия через D[X], Dx, D(X)). Таким образом, по определению

На практике дисперсию удобно находить по формуле: DX=MX²-(MX)².

Свойства дисперсии:

1. Дисперсия постоянной равна 0, т.е.

Dc=0.

2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат, т.е.

DcX=c²DX

3. Дисперсия суммы независимых случайных величин равно сумме их дисперсий, т.е. если Х и Y независимы, то

D(X+Y)=DX+DY

4. Дисперсия случайных величин не изменится, если к этой случайной величине прибавить постоянную, т.е.

D(X+c)=DX

5. Если случайные величины X и Y независимы, то

D(XY)=MX²*MY²-(MX⁾²*(MY)²

8.4 Распределения Пирсона и их основные характеристики

Распределением χ²_n с n степенями свободы называется распределение суммы квадратов n независимых стандартных случайных величин, т.е.

Плотность вероятности случайных величин χ² зависит только от числа n, т.е. числа слагаемых. Если n=1, то χ²=Х², где Х ~ N(0,1),

Плотность распределения случайной величины Y = Х² равна

Плотность распределения χ²_n имеет вид

для целых положительных р)

С возрастанием числа степеней свободы n распределение χ² приближается к нормальному закону распределения ( при n>30 распределение χ² практически не отличается от нормального);

На практике, как правило, можно использовать не плотность вероятности, а квантили распределения χ²

Квантилью распределения χ²_n , отвечающей уровню значимости ά, называется такое значение χ²_n = χ²_{n ά}, при котором

С геометрической точки зрения нахождения квантили = χ²_{n ά} заключается в выборе такого значения χ²_n = χ²_{n ά,} чтобы площадь заштрихованной фигуры была равно ά.

Для стандарного нормального распределения квантили уровня ά обозначаются через «плюс-минус»u_ά, причем u_ά является решением уравнения

8.5 Распределения Стьюдента и их основные характеристики

Распределением Стьюдента (или t-распределением) с n степенями свободы называется распределение случайных величин

где Z ~ N(0,1) – стандартная нормальная величина, независимая от χ²_n-распределения.

Плотность вероятности распределения Стьюдента имеет вид

При n→∞ распределение Стьюдента приближается (уже при n>30 почти совпадает) к нормальному

На практике использую квантили t-распределения: такое значение

С геометрической точки зрения нахождение квантилей заключается в выборе такого значения , чтобы площадь заштрихованной фигуры была равна ά.

9.1. Неравенство Чебышева.

Теорема 5.1. Если с.в. Х имеет м.о. МХ=а и дисперсию DХ, то для любого ε>0 справедливо неравенство Чебышева P{|Х-MX|≥ε}≤DX/ε². (5.1.)

9.2. Неравенство Маркова.

МАРКОВА НЕРАВЕНСТВО

для производной от алгебраического многочлена - неравенство, дающее оценку максимального значения этой производной через наибольшее значение самого многочлена. Пусть Р _п (х).- алгебраич. многочлен степени не выше пи 

Тогда для любого хиз отрезка [ а, b]выполняется неравенство 

Неравенство (*) получено А. А. Марковым в 1889 (см. [1]). М. н. является точным. Так, если a= -1, b=1, то 

и в неравенстве (*) достигается знак равенства.

Для производной любого порядка   из М. н. следует соотношение 

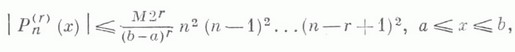
к-рое при   уже не является точным. Точное неравенство для   получено В. А. Марковым [2]:

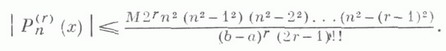
9.3.Теорема Чебышева.

9.4. Теорема Бернули.

9.5. Центральная предельная теорема.

10.1. Понятие случайного процесса.