
Свойства коэффициента эксцесса
 .
.Пусть
 — независимые случайные
величины с равной дисперсией.
Пусть
— независимые случайные
величины с равной дисперсией.
Пусть  .
Тогда
.
Тогда
![]() ,
,
где ![]() —
коэффициенты эксцесса соответствующих
случайных величин.
—
коэффициенты эксцесса соответствующих
случайных величин.

6.1 Биноминальный закон распределения и его базовые характеритики
Биномиа́льное
распределе́ние в теории
вероятностей — распределение количества
«успехов» в последовательности
из ![]() независимых случайных
экспериментов,
таких что вероятность «успеха»
в каждом из них постоянна и равна
независимых случайных
экспериментов,
таких что вероятность «успеха»
в каждом из них постоянна и равна ![]() .
.
Свойства биномиального распределения
Пусть
 и
и  .
Тогда
.
Тогда 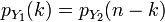 .
.Пусть
 и
и 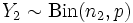 .
Тогда
.
Тогда 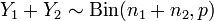 .
.
6.2 Распределение Пуассона и его базовые характеристики
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Свойства распределения Пуассона
Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть
 .
Тогда
.
Тогда
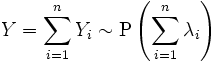 .
.
Пусть
 ,
и
,
и  .
Тогда условное
распределение
.
Тогда условное
распределение  при
условии, что
при
условии, что 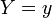 ,
биномиально. Более точно:
,
биномиально. Более точно:
![]() .
.
6.3 Геометрическое распределение и его базовые характеристики
Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».
Свойства геометрического распределения
Из всех дискретных распределений с фиксированным средним
 геометрическое
распределение
геометрическое
распределение  является
одним из распределений с
максимальной информационной
энтропией.
является
одним из распределений с
максимальной информационной
энтропией.Если
 независимы
и
независимы
и 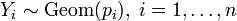 ,
то
,
то
 .
.
Геометрическое распределение бесконечно делимо.
7.3 ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИЫ.
Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию gi из U сопоставим несколько чисел: ξ i1 , ξ i2 , ξ i3 , ... ξ ik или вектор ξi. Потребуем, чтобы для любых хj ( -∞ < хj <+∞ ) , j = 1, 2 ... k , множество А тех g , для которых ξ j < хj ( j = 1, 2, ... k) , принадлежало полю событий, т.е. для него определена вероятность Р{ ξ 1 < x1 , ξ 2 < x2 , ... ξ k < xk } = P(A) = F( x1, x2, ... xk ). Тогда ξ называется многомерной случайной величиной, или случайным вектором, а F( x1, x2, ... xk ) еефункцией распределения.
Примеры: 1 . Координаты молекулы, находящейся в сосуде с газом, (x,y,z) или компоненты ее скорости (Vx,Vy,Vz) - можно рассматривать как трехмерные случайные величины 2 . В задаче "о встрече" время прихода одного участника (х1) и другого (х2), если условия их прихода известны (скажем - любой момент в течение заданного часа), пару чисел х1, х2 можно рассматривать как двумерную случайную величину 3 . Результат эксперимента, состоящего в измерении тока через разрядную трубку при десяти различных напряжениях, поданных на трубку, можно рассматривать как десятимерную случайную величину
Свойства многомерной функции распределения: 1 . F( x1, x2, ... -∞ ... xk ) = 0; 2 . F( x1, x2, ... xk-1, ∞) = F( x1, x2, ... xk-1 ), т.е. если один из аргументов принимает значение ∞, то размерность случайной величины уменьшается на 1; 3 . F( x1, x2, ... xk ) не убывающая функция любого аргумента.


7.5. Основной способ описания дискретной многомерной случайной величины
