3.3

Геометрические вероятности

При геометрическом подходе к определению вероятности в качестве пространства  элементарных событий рассматривается произвольное множество конечной лебеговой меры на прямой, плоскости или пространстве. Событиями называются всевозможные измеримые подмножества множества   .

Вероятность события А определяется формулой

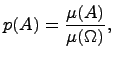
где   обозначает лебегову меру множества А. При таком определении событий и вероятностей все аксиомы А.Н.Колмогорова выполняются.

В конкретных задачах, которые сводятся к указанной выше вероятностной схеме, испытание интерпретируется как случайный выбор точки в некоторой области   , а событие А – как попадание выбранной точки в некоторую подобласть А области   . При этом требуется, чтобы все точки области   имели одинаковую возможность быть выбранными. Это требование обычно выражается словами «наудачу», «случайным образом» и т.д.

3.4

Алгебра событий (в теории вероятностей) — алгебра подмножеств пространства элементарных событий  , элементами которого служат элементарные события.

Как и положено алгебре множеств алгебра событий содержит невозможное событие (пустое множество) и замкнута относительно теоретико-множественных операций, производимых в конечном числе. Достаточно потребовать, чтобы алгебра событий была замкнута относительно двух операций, например, пересечения и дополнения, из чего сразу последует её замкнутость относительно любых других теоретико-множественных операций. Алгебра событий, замкнутая относительно счётного числа теоретико-множественных операций, называется сигма-алгеброй событий.

3.6

Несовместные  (несовместимые) события  - это события, для которых наступления одного из них  исключает наступление других в одном и том же испытании, т.е. они не могут появиться вместе.

События  А и В называются  несовместными ( А   В =   ) , если их одновременное появление невозможно. Например, выпадение и "решки", и "орла" при бросании монеты.

3.7 Что такое «независимая величина»?

Событие A называется независимым от события B, если возможность наступления события A не зависит от того, произошло событие B или нет.

В противном случае события являются зависимыми. Условной вероятностью события B при наличии A называется величина

(при этом полагается, что P(A) не равно 0).

Условную вероятность события P(B/A) можно трактовать как вероятность события B, вычисленная при условии, что событие A произошло.

Заметим, что если имеется несколько событий A1, A2, …, An, то их попарная независимость (т.е. независимость любых двух событий Ai и Aj, i≠j) еще не означает их независимости в совокупности.

3.8 Понятие условной вероятности.

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Пусть А и В- два события, рассматриваемые в данном опыте. Наступление одного события(скажем,А)может влиять на возможность наступления другого (В).Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Условной вероятностью события В при условии, что произошло события В при условии, что произошло событие А, называется отношение вероятности события А, причём Р(А) ≠0,обозначается символом Р(В\А).

Таким образом, по определению

Р(В\А)= Р(ВА) /Р(А), Р(А) ≠0

Вероятность Р(В), в отличие от условной, называется безусловной вероятностью.

Аналогично определяется условная вероятность события А при условии В, т.е Р(А\В)

Р(А\В)= Р(АВ) /Р(В), Р(В) ≠0

3.9 Формула полной вероятности.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Пусть дано вероятностное пространство  , и полная группа попарно несовместных событий  , таких что            . Пусть   — интересующее нас событие. Тогда

.

Формула полной вероятности также имеет следующую интерпретацию. Пусть   — случайная величина, имеющая распределение

.

Тогда

,

т.е. априорная вероятность события равна среднему его апостериорной вероятности.

3.10 Формула Байеса.

Формула Байеса:

,

где

 — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

 — вероятность наступления события B при истинности гипотезы A;

 — полная вероятность наступления события B.

3.13 ФОРМУЛА БЕРНУЛЛИ

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.

Формулировка

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна: , где .

Доказательство

Так как в результате независимых испытаний, проведенных в одинаковых условиях, событие наступает с вероятностью , следовательно, противоположное ему событие с вероятностью .

Обозначим  — наступление события в испытании с номером . Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате опытов событие наступает раз, тогда остальные раз это событие не наступает. Событие может появиться раз в испытаниях в различных комбинациях, число которых равно количеству сочетаний из элементов по . Это количество сочетаний находится по формуле:

.

При этом вероятность каждой комбинации равна произведению вероятностей:

.

Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:

, где .

Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,7. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии в продолжении каждых из 6 суток постоянна и равна р=0,7. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q =1 – p = 1 – 0,7 = 0,3.

Из условия задачи следует, что n = 6; k=4.

Искомая вероятность по формуле Бернулли равна:

.

3.14 Где находится максимум вероятности в формуле Бернулли?

Отметим, что вероятности Pn(k) совпадают с соответствующими членами разложения бинома (p + q)ⁿ по степеням p:

Поэтому распределение вероятностей (по различным значениям k) называют биномиальным законом распределения вероятностей. Из этого соотношения следует, что сумма всех вероятностей равна единице (условие нормировки вероятностей), так как (p + q)ⁿ = 1ⁿ= 1.

Каждое из чисел k (k = 0, 1, 2, …, n) имеет свою вероятность при проведении последовательности независимых испытаний. Число s, которому соответствует наибольшая вероятность P_n(k), называется наивероятнейшим числом появлений события в последовательности n независимых испытаний. По определению, P_n(s) ≥ P_n(s – 1) и P_n(s) ≥ P_n(s + 1).

Раскрывая эти неравенства и упрощая их, получим:

np − q ≤ s ≤ np + p.

Если границы промежутка определяются дробными числами, то в промежутке

имеется одно целое число, которое и является наивероятнейшим числом. Если границы

определяются целыми числами, то существует два наивероятнейших числа: s1 = np – q и

s2 = np + p.

3.15 ТЕОРЕМА ПУАССОНА

Теорема Пуассона

Пусть производится n независимых испытаний, в каждом из которых событие появляется с постоянной вероятностью p, причем p→0 или p→1 (близка к 0 или близка к 1)

Теорема. Если вероятность p_n→0, при n→∞ , то вероятность p_n(k) (в n испытаниях событие наступает ровно k раз): p_n(k)≈ (λ^k / k!)* e^−λ, где λ=n*p 

Доказательство.

p_n(k)=C_n^k*p^k *(1−p)^n−k, 

т.к. p=λ/n, то p_n(k)= (n! /k!(n−k)!)*(λ/n)^k*(1−λ/n)^n−k= (λ^k / k!) * (n(n−1)...(n−k+1))/ n^k*(1−λ/n)ⁿ(1−λ/n)^−k 

Взяв предел от последнего выражения получим искомую формулу:

Lim p_n(k)= (λ^k / k!)*e^−k

n→∞

3.16 Локальная Теорема Муавра — Лапласа

Локальная Теорема Муавра — Лапласа — одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина ограничена равномерно по m и n , то

где , c > 0, c — постоянная.

Приближённую формулу

рекомендуется применять при n > 100 и npq > 20.

Доказательство

Для доказательства Теоремы будем использовать формулу Стирлинга из математического анализа:

(1) где . При больших величина очень мала, и приближённая формула Стирлинга, записанная в простом виде,

(2) даёт малую относительную ошибку, быстро стремящуюся к нулю, когда .

Нас будут интересовать значения , не очень отличающиеся от наивероятнейшего. Тогда при фиксированном условие будет так же означать, что

, (3)

Поэтому использование приближённой формулы Стирлинга для замены факториалов в биномиальном распределении допустимо, и мы получаем

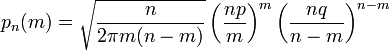(4)

Также понадобится использование отклонения относительной частоты от наивероятнейшего значения

(5)

Переписываем полученное ранее биномиальное распределение с факториалами, заменёнными по приближённой формуле Стирлинга:

(6)

Предположим, что

(7)

Взяв логарифм второго и третьего множителей равенства (6), применим разложение в ряд Тейлора:

(8)

Располагаем члены этого разложения по степеням :

(9)

Предположим, что при

(10)

Это условие, как уже было указанно выше, означает, что рассматриваются значения , не очень далёкие от наивероятнейшего. Очевидно, что (10) обеспечивает выполнение (7) и (3).

Теперь, пренебрегая вторым и последующими членами в разложении (6), получаем, что логарифм произведения второго и третьего членов произведения в правой части (8) равен

(11)

Отбрасывая малые слагаемые в скобках первого множителя (6), получаем:

(12)

Обозначив

(13)

Переписываем (12) в виде:

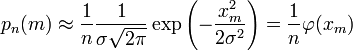(14)

Где  — нормальная функция.

Поскольку в интервале имеется только одно целое число , то можно сказать, что есть вероятность попадания в интервал . Из (5) следует, что изменению на 1 соответствует изменение на

(15)

Поэтому вероятность попадания в интервал равна вероятности попадания в промежуток

(16)

Когда , и равенство (16) показывает, что нормальная функция является плотностью случайной переменной

Таким образом, если то для отклонения относительной частоты от наивероятнейшего значения справедлива асимптотическая формула (16), в которой  — нормальная функция с и .

Таким образом теорема доказана.

3.17 ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА

4.1 Cведение описания статистик к описанию случайных величин

Основные способы математического описания случайных величин

Величина х, принимающая в каждом новом опыте при одинаковых условиях его проведения новое значение, называется случайной величиной (СВ), а конкретное значение x _х, которое она принимает в результате опыта –реализацией случайной величины. Совокупность реализаций СВ x _х(1),…, x _х(N),которая получается в результате проведения N опытов, называется выборкой реализации СВ х объема N [1].

Под вероятностью появления в результате опыта значения Х случайной величиных будем понимать относительную частоту попадания реализаций x _х в бесконечно малый интервал (Х, Х+dХ) для выборки реализаций бесконечно большого объема.

Полной характеристикой скалярной СВ х является плотность распределения вероятности СВ p_x(X), характеризующая относительную вероятность попадания реализации x _х СВ в бесконечно малый интервал (Х, Х+dХ) :

, (1.1)

где Х – фиксированное значение СВ х,

а также функция распределения вероятности СВ F_x(Х)=P(x _х£ Х), связанная сp_x(Х) соотношением

. (1.2)

Свойства плотности распределения вероятности p_x(Х) скалярной СВ х:

- p_x(Х)³ 0;

- p_x(Х) =0 при Х=± ¥ ;

- знание p_x(Х) позволяет вычислить вероятность события Р(a£ x£ b) :

; (1.3)

- p_x(Х) удовлетворяет условию нормировки –  . (1.4)

Для векторных случайных величин х= (x₁,...,x_n), где x₁,...,x_n – скалярные СВ (компоненты векторной СВ), вводятся аналогичные понятия [2].

Полной характеристикой векторной СВ х= (x₁,...,x_n) является n-мернаясовместная плотность распределения вероятности р_x(Х) = р_x(Х₁,...,Х_n), имеющая интерпретацию и свойства аналогичные скалярной СВ:

- р_x(Х₁,...,Х_n) ³ 0 (неотрицательная функция n аргументов);

- р_x(Х₁,...,Х_n) =0 при Х_j=± ¥ , где j изменяется от 1 до n;

- знание р_x(Х₁,...,Х_n) позволяет вычислить вероятность события

, (1.5)

где D – заданная область в n-мерном пространстве переменной Х;

- р_x(Х₁,...,Х_n) удовлетворяет условию нормировки

. (1.6)

В дальнейшем, если это не оговаривается отдельно, для функции плотности распределения вероятности и функции распределения вероятности будут использоваться следующие упрощенные обозначения - р(х) вместо р_х(X), F(x)вместо F_x(X)

Для векторных СВ вводится дополнительная система понятий, отображающая взаимосвязь между отдельными ее компонентами. Если в векторной СВ хразмерности n выделить две векторные СВ меньшей размерности y=(x₁,..,x_k) и z=(x_k+1,...,x_n), то для отображения свойств этих отдельных векторных СВ рассматриваются соответствующие совместные плотности распределения вероятности меньших размерностей :

, (1.7)

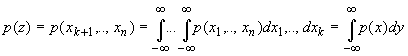. (1.8)

Вводится понятие условной плотности распределения вероятности p(y/Z)СВ y в предположении, что СВ z приняла значение Z, которая связана с совместной плотностью распределения р(х)=p(y,z) соотношением

. (1.9)

Аналогично можно ввести понятие условной плотности распределения вероятности p(z/Y) для СВ z в предположении, что СВ y приняла значение Y:

. (1.10)

На основании соотношений (1.7)–(1.10) можно выразить одну условную плотность распределения вероятности через другую (формулы Байеса) :

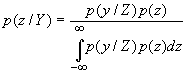,  . (1.11)

Случайные величины y и z называются независимыми, если выполняется условие

р(y/Z)=р(y); р(z/Y)=р(z). (1.12)

Отсюда для независимых СВ y и z совместная плотность распределения вероятности р(х) может быть найдена по соотношению

р(x) = p(y,z)= р(y)р(z), (1.13)

а если все компоненты векторной СВ х= (x₁,...,x_n) являются независимыми скалярными СВ, то можно записать

, (1.14)

где р(х_i) – плотность распределения вероятности соответствующей скалярной СВх_i.

Описания свойств и действия с СВ удобнее производить, используя их моментные характеристики, которые являются детерминированными величинами, вместо плотности распределения вероятности. Однако при этом снижается полнота информации о СВ. Чем выше порядок моментных характеристик, которыми характеризуется СВ, тем больше имеется о ней информации.

Общее выражение для определения моментной характеристики СВ x, которую можно представить в виде функции f(x), имеет вид

. (1.15)

Для скалярных СВ наиболее часто используются следующие моментные характеристики.

Математическое ожидание СВ М_х – определяет наиболее вероятное значение реализации СВ x, т.е. в выражении (1.15) положено f(x)=x :

. (1.16)

Элементарные свойства математических ожиданий СВ:

- если С – константа, то M[C] = C,

- если y = Сx и С – константа, то M_y = СM_x, (1.17)

- если  , то  ,

Дисперсия СВ D_x – характеризует наиболее вероятный разброс реализаций СВ xотносительно её математического ожидания, т.е. в выражении (1.15) положено f(x) = (x – M_x)² :

. (1.18)

Для сохранения размерности исходной СВ удобно рассматривать в качестве меры разброса реализаций среднеквадратическое отклонение СВ :

. (1.18")

Для двух скалярных СВ, например x и y, вводится понятие взаимный ковариационный момент K_xy , отражающий статистическую взаимосвязь между ними :

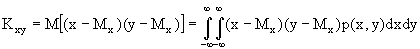. (1.19)

Если K_xy=0 для скалярных СВ x и y, то такие СВ называютсянекоррелированными.

Если скалярные СВ x и y являются независимыми, т.е. p(x, y) = p(x)p(y)), то из (1.19) следует, что K_xy = 0, т.е. они являются также некоррелированными.

Часто вместо K_xy рассматривают нормированный ковариационный момент(или коэффициент корреляции) :

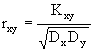,  . (1.20)

Элементарные свойства дисперсий СВ :

- если С – константа, то D[С] = 0,

- если y = Cx и С – константа, то D_y = С²D_x,

- если  , то  (1.21) (если y = x₁ + x₂, то  ),

- если   и x₁, …, x_n – некоррелированные СВ, то  .

Аналогично вводятся моментные характеристики для векторных СВ

х = (x₁, …, x_n).

Математическое ожидание векторной СВ х=(x₁,…,x_n) есть вектор-столбец математических ожиданий ее компонент, т.е.  .

Ковариационная матрица векторной СВ х=(x₁,…, x_n) (аналог дисперсии для скалярной СВ) есть симметричная относительно главной диагонали квадратная матрица размера n´ n вида

. (1.22)

Также часто используется нормированная ковариационная матрица R_x(матрица коэффициентов корреляций) :

, (1.23)

(если векторная СВ x имеет некоррелированные компоненты, то R_x = Е – единичная матрица).

4.2 Функция распределения как универсальный способ описания случайной величины

Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.      Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.      F(x) = P (X <x). Иногда функцию F(x) называют интегральной функцией распределения.

4.3 Основные свойства функции распределения случайной величины

 Функция распределения обладает следующими свойствами:      1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.      2. Функции распределения есть неубывающая функция.      3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:       Р(а < X < b) = F(b) – F(а).                                          (2.1)      4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то       F(x) = 0 при х ≤ а ;F(x) = 1 при х ≥ b.      5. Справедливы следующие предельные отношения:       .

4.4 Основной способ описания дискретной случайной величины

Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.

Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σp_i = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (x_i; p_i)

Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X) = P(ξ < X). Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины.

4.5 Специфические свойства функции распределения дискретной случайной величины

Функция называется функцией распределения случайной величины Х.

Для дискретной случайной величины

,

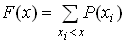
(1.23)

где     x_i - значения, принимаемые случайной величиной Х;

P(x_i) - значения вероятностей при X  = x_i;

х - некоторое фиксированное значение Х.

Свойства функции распределения вытекают из аксиом вероятностей и их следствий и определяются в виде:

1. , .

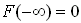2. Если a<b, то 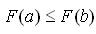для любых значений a и b (функция неубывающая).

При решении практических задач часто возникает необходимость вычислять вероятность того, что случайная величина примет значение в интервале от a до b или . Эта вероятность выражается через F(x) следующим образом.

Пусть событие А состоит в том, что X<b, событие В состоит в том, что X<a, событие С состоит в том, что .

Учитывая, что A = B + C, по теореме сложения вероятностей имеем или , отсюда

.

(1.24)

4.6 Основной способ описания непрерывной случайной величины

Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.

Плотность вероятности непрерывной случайной величины, она же дифференциальная функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией (многоугольник распределения), то плотность вероятностей графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Аналитически задаётся формулой. Если закон распределения дискретной с.в. ставит каждому значению x в соответствие определённую вероятность, то про плотность распределения такого сказать нельзя. Для непрерывных с.в. можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного (одиночного) значения непрерывной с.в. вероятность равна нулю. И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом. Свойства плотности вероятности: 1) Значения функции неотрицательны, т.е. f(x)≥0 2) Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1).

4.7 Специфические свойства функции распределения непрерывной случайной величины

Непрерывной случайной величиной называется случайная величина, которая может принять любое значение из заданного числового отрезка.

Вероятность любого отдельного значения непрерывной случайной величины равна нулю. Этот вывод можно получить из соотношения (1.24), согласно которому для дискретных случайных величин.

Если неограниченно уменьшать отрезок (a, b), полагая , то в пределе получим не вероятность попадания на участок, а вероятность того, что случайная величина X = a, т. е.

.

Если функция F(x) непрерывна в точке а, то этот предел равен нулю.

Непрерывными случайными величинами называют еще величины, функция распределения которых везде непрерывна. Таким образом, обладать нулевой вероятностью могут не только невозможные (как определялось ранее), а и возможные события. Это появляется при рассмотрении экспериментов, не сводящихся к схеме случаев.

Как указывалось ранее, закон распределения для непрерывной случайной величины может быть задан с помощью функции распределения.

Кроме этого, для задания закона распределения непрерывной случайной величины используется функция f(x) = F^/(x), которая называется плотностью вероятности и которая является производной от функции распределения. Поэтому ее еще называют дифференциальной функцией, а функцию распределения называют интегральной функцией.

Кривая, изображающая плотность распределения, называется кривой распределения; пример кривой распределения представлен на рис. 1.7.

Рис. 1.7. График плотности распределения, или кривая распределения

Вероятность попадания непрерывной случайной величины на отрезок от a до b определяется в виде

.

(1.25)

Геометрически вероятность попадания случайной величины X на участок (a, b) равна площади под кривой распределения, опирающейся на этот участок (см. рис. 1.8).

Рис. 1.8. Геометрическая интерпретация вероятности попадания случайной величины на отрезок от a до b

Заметим, что f(c) - величина плотности распределения в точке с - не определяет значение P(X=c), как в случае дискретной случайной величины. Для непрерывных случайных величин вероятность определяется для некоторого интервала и, как уже указывалось, P(X=c) = 0 для любого значения с.

Из этого следует, что не имеет значения, включаются точки a и b в интервал или нет, т. е.

.

Свойства плотности вероятности

Из аксиом вероятности следует, что плотность вероятности f(x) непрерывной случайной величины Х удовлетворяет:

1. для .

2. .

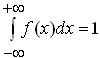Функция распределения непрерывной случайной величины Х с плотностью распределения f(x) определяется в виде

(1.26)

для .

Свойства функции распределения для непрерывной случайной величины такие же, как для дискретной случайной величины, т. е.

5.1 характеристики случайной величины как формальные характеристики соответствующий статистики

5.2 определение математического ожидания для вариантов дискретной и непрерывной случайной величины

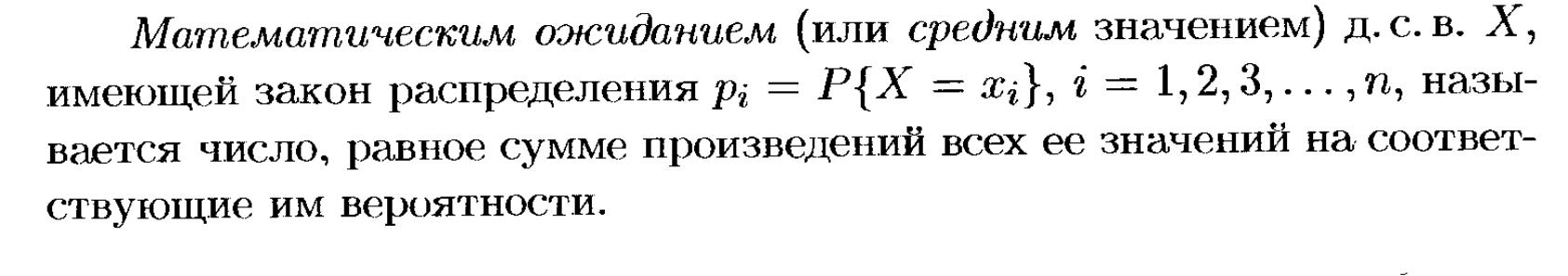
Математическое ожидание дискретного распределения

• Если   — дискретная случайная величина, имеющая распределение

,

то прямо из определения интеграла Лебега следует, что

.

Математическое ожидание абсолютно непрерывного распределения

• Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью  , равно

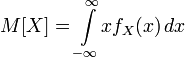
Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.

X			…
P			…

 

 

 

 

Т.е., если сл. величина имеет закон распределения, то

называется её математическим ожиданием. Если сл. величина имеет бесконечное число значений, то математическое ожидание определяется суммой бесконечного ряда  , при условии, что этот ряд абсолютно сходится (в противном случае говорят, что математическое ожидание не существует).

Для непрерывной сл. величины, заданной функцией плотности вероят­ности f(x), математическое ожидание определяется в виде интеграла

при условии, что этот интеграл существует (если интеграл расходится, то говорят, что математическое ожидание не существует).

5 .3 основные свойства математического ожидания на пространстве случайных величин

5.4 определение дисперсии и среднего квадратического отклонения для вариантов дискретной и непрерывной случайной величины

5.5 формула расчета дисперсии через использование второго момента случайной величины

5.6 основные свойства дисперсии на пространстве случайной величины

5.7 понятие центрированной , нормированной, стандартной случайной величины

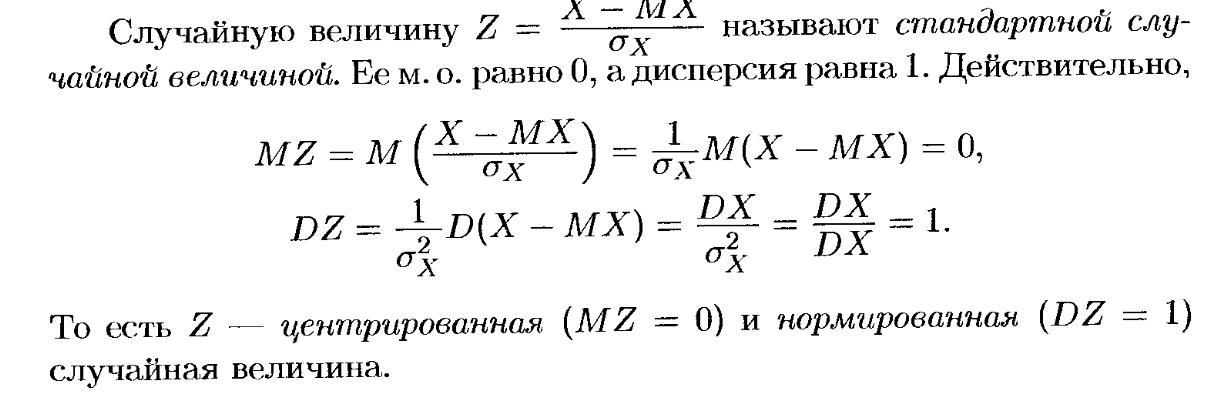
Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания.

Центрированная величина обладает двумя удобными для преобразования свойствами:

Нормированная случайная величина (z) есть центрированная случайная величина, измеренная в масштабе стандартных отклонений  :

4.1.4

Нормированная случайная величина также отличается двумя свойствами:

Математическое ожидание стандартной случайной величины равно нулю, ее среднеквадратичное отклонение равно единице. Стандартная случайная величина иногда трактуется как коэффициент надежности. При этом требуется, чтобы вероятность превышения заданного т данной случайной величиной была меньше допустимой.

5.8 понятие моды и медианы случайной величины

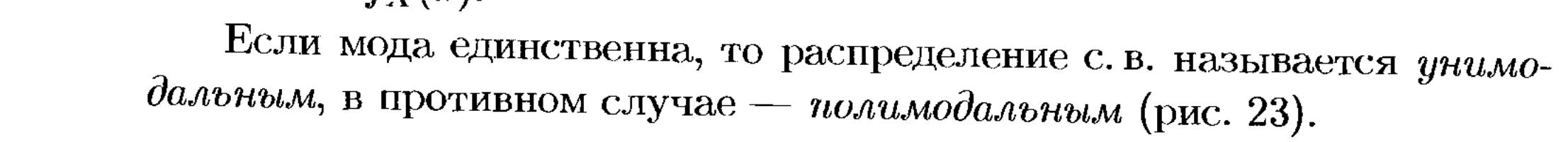
Модой (Мо) случайной величины х называется наиболее вероятное ее значение. Это определение строго относится к дискретным случайным величинам. Для непрерывной величины модой называется такое ее значение для которого функция плотности распределения имеет максимальную величину.

Медианой (Ме) случайной величины называется такое ее значение для которого окажется ли случайная величина меньше этого значения. Для непрерывной случайной величины медиана это абсцисса точки в которой площадь под кривой распределяется пополам. Для дискретной случайной величины значение медианы зависит от того четное или нечетное значение случайной величины n=2k+1, то Ме=х_к+1 (среднее по порядку значение) Если значение случайных величин четное, т.е  n=2k, то Me=(x_k+x_k+1)/2

5.9 понятие коэффициентов асимметрии и и эксцесса случайной величины