16) Коэффициент вариации, медиана, мода.

Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:

,

где - искомый показатель, - среднее квадратичное отклонение, - средняя величина.

 Мода

Под модой в статистике понимается значение признака или вариант, который чаще всего встречается в данной совокупности.

В дискретном ряду распределения модой является вариант, обладающий наибольшей частотой.

Выбирается модальный интервал.

 

Рассчитывается значение моды по формуле

M_O=x_n+[h_(M_O)]*(Fmo-Fmo-1)/((Fmo-fmo-1)+(Fmo-Fmo+1)) Hmo-величина модалшьного интервала xmo – нижняя граница интервала. Fm0 -Это частоты модального, предмодального и послемодального интервала.

Медиана

Под медианой понимается значение признака или вариант, который находится в середине ранжированного, т.е. упорядоченного рядораспределения. Медиана делит ряд на 2 равные части, по количеству единиц совокупности, при этом у одной половины единиц значение признака меньше медианы, а у второй половины единицы больше медианы. Для дискретного рядораспределения с нечётным количеством членов n номер медианного варианта определяется как (n-1)/2. Если n четная, то медианой будет являются среднее значение 2 вариантов n/2 и n/2-1.

Медиана равна 680 000 руб. Расчёт медианы в интервальном ряду распределения осуществляется в 2 этапа. Выделяется медианный интервал и рассчитывается значение медианы по формуле. Ме=Xme+hme ( (∑f)/2-Sme-1)/Fme Hme – ширина медианного интервала. (∑f)/2 – сумма частот ряда. Sme – сумма накопленного ряда предшествующих медиане. Частота медианного интервала.

17) Биноминальное распределение и его свойства.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна .

Определение

Пусть  — конечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину :

.

Тогда , число единиц (успехов) в последовательности , имеет биномиальное распределение с степенями свободы и вероятностью «успеха» . Пишем: . Её функция вероятности задаётся формулой:

где  — биномиальный коэффициент.

Свойства биномиального распределения

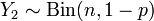• Пусть и . Тогда .

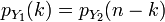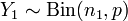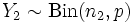• Пусть и . Тогда

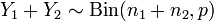
18) Распределение Пуассона и его свойства.

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение

Выберем фиксированное число и определим дискретное распределение, задаваемое следующей функцией вероятности:

,

где

• обозначает факториал числа ,

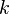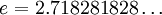•  — основание натурального логарифма.

Тот факт, что случайная величина имеет распределение Пуассона с параметром , записывается: .