13) Плотность распределения и ее свойства.

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.

Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.

Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:

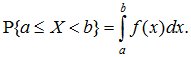(5.7)

В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β) (рис. 5.4).

Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

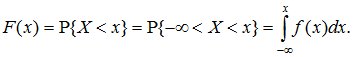(5.8)

В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x (рис. 5.5).

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) ³ 0.

Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.

2. Условие нормировки: 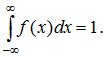Это свойство следует из формулы (5.8), если положить в ней x=∞.

Геометрически основные свойства плотности f(x) интерпретируются так:

1. вся кривая распределения лежит не ниже оси абсцисс;

2. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

 

14) Математическое ожидание, его свойства.

Математическое ожидание, среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений y₁, y₂, ..., y_k, ... с вероятностями, равными соответственно p₁, p₂, ..., p_k, …, М. о. определяется формулой

(в предположении, что ряд  сходится). Так, например, если Х — число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью ¹/₆), то .

Для случайной величины, имеющей плотность вероятности р(у), М. о. определяется формулой

.

Свойства математического ожидания.

1) Математическое ожидание постоянной величины равно самой постоянной.

            2) Постоянный множитель можно выносить за знак математического ожидания.

            3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

            Это свойство справедливо для произвольного числа случайных величин.

            4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.

        Это свойство также справедливо для произвольного числа случайных величин.

15) Дисперсия, ее свойства.

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается в русской литературе и (англ. variance) в зарубежной.

Определение

Пусть  — случайная величина, определённая на некотором вероятностном пространстве. Тогда

где символ обозначает математическое ожидание^[1][2].

• Дисперсия любой случайной величины неотрицательна:

• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

• Если случайная величина равна константе, то её дисперсия равна нулю: 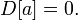Верно и обратное: если 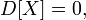то почти всюду;

• Дисперсия суммы двух случайных величин равна:

, где  — их ковариация;

• Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

, где ;

• В частности, 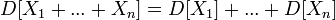для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;

• 

• 

•