Свойства

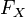• непрерывна справа:^[1]

• не убывает на всей числовой прямой.

• .

• .

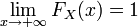• Распределение случайной величины однозначно определяет функцию распределения.

  • Верно и обратное: если функция удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что является её функцией распределения.

• По определению непрерывности справа, функция имеет правый предел в любой точке , и он совпадает со значением функции 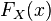в этой точке.

  • В силу неубывания, функция также имеет и левый предел 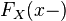в любой точке , который может не совпадать со значением функции. Таким образом, функция либо непрерывна в точке, либо имеет в ней разрыв первого рода.

12) Дискретные и непрерывные случайные велечины. Дискретные случайные величины

     Определение1: Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Задание дискретной случайной величины по определению равносильно заданию закона распределения случайной величины в следующем виде:

    

где

Следующее утверждение отражает связь между функцией распределения дискретной случайной величины и законом распределения случайной величины.

     Утверждение 1: Закон распределения и функция распределения дискретной случайной величины взаимно однозначно определяют друг друга.

Примеры дискретных случайных величин:

1) дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1

Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1.

Непрерывные случайные величины

 

     Определение 2: Распределение случайной величины называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого

,

где - интегрируемая по Лебегу функция. Функция называется плотностью распределения случайной величины .

     Теорема 1: Для того чтобы случайная величина была непрерывной случайной величиной, необходимо и достаточно, чтобы для любого

         (1)

     Замечание 1: Из представления (1) видно, что функция распределения непрерывной случайной величины является непрерывной функцией.

   

    Свойства плотности распределения:

1)

2) почти всюду.

3) для любых х, являющихся точками непрерывности плотности.

 

     Теорема 2: Для того, чтобы функция p = p(x) была плотностью распределения некоторой случайной величины , необходимо и достаточно, чтобы она удовлетворяла свойствам 1) и 2) плотности.

1) нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение). Непрерывная случайная величина имеет нормальное (гауссовское) распределение, если её плотность распределения имеет вид

     Если , то распределение называется стандартным нормальным распределением.

     Важная роль этого распределения объясняется тем, что оно обычно возникает в явлениях, подверженных действию большого числа малых случайных величин. Так, математическая теория выборочного метода в статистике для расчета некоторых показателей широко использует нормальное распределение.