Тема 3.2. Решение задач дискретного программирования
Теоретические сведения
Общая постановка задачи дискретного программирования (на примере задачи максимизации):
Найти
при условиях
(10.12)
где D - некоторое множество R(n)
Если множество D является конечным или счетным, то условие (10.12) - это условие дискретности, и данная задача является задачей дискретного программирования (ЗДП). Чаще всего условие дискретности разделено по отдельным переменным следующим образом:
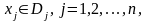
где D - конечное (или счетное) множество.
Если вводится ограничение х; - целые числа (j=l,2,..., n), то приходят к задачам целочисленного программирования (ЦП), которое является частным случаем дискретного программирования.
Для решения задач дискретного программирования нужно применить метод ветвей и границ [1-3].
Задача 2. Решите следующие задачи дискретного программирования
Постройте дерево подзадач, получаемое при использовании метода ветвей и границ, для каждой из приведенных ниже задач.
Максимизировать f(x)=3x1+2x2
при ограничениях
2x1+5x2≤9,
4x1+2x2≤9,
x1, x2 - 0 и целые.
2) Максимизировать f(x)=2x1+3x2
при ограничениях
5x1+7x2≤35,
4x1+9x2≤36,
x1, x2 - 0 и целые.
3) Максимизировать f(x)= x1+x2
при ограничениях
2x1+5x2≤16,
6x1+5x2≤27,
x1, x2 - 0 и целые.
4) Минимизировать f(x)=5x1+4x2
при ограничениях
3x1+2x2≥9,
2x1+3x2≥7,
x1, x2 - 0 и целые.
5) Максимизировать f(x)= 5x1+7x2
при ограничениях
2x1+x2≤13,
6x1+9x2≤41,
x1, x2 - 0 и целые.
6) Максимизировать f(x)= 5x1+4x2
при ограничениях
x1+x2≤5,
10x1+6x2≤45,
x1, x2 - 0 и целые.
7) Максимизировать f(x)= 5x1+6x2
при ограничениях
10x1+7x2≤35,
5x1+14x2≤35,
x1, x2 - и целые.
8) Максимизировать 3x1+3x2 +13x3
При ограничениях -3 x1+6 x2+7 x3≤8;
6 x1-3 x2 +7 x3≤8;
где каждая переменная xj должна быть неотрицательным целым.
Контрольные вопросы
Сформулируйте постановку задачи дискретного линейного программирования.
Опишите особенности задач дискретного линейного программирования.
Сформулируйте постановку задачи дискретного нелинейного программирования с неделимостями.
Что такое метод ветвей и границ?
Опишите решение задач дискретного линейного программирования методом ветвей и границ.
Сформулируйте постановку задачи о назначениях.
Опишите алгоритм поиска оптимального решения задачи о назначениях.
Практическое занятие 4 Тема. Решение задач динамического программирования
Теоретические сведения
Рекуррентное уравнение для вычисления кратчайшего расстояния до узла xi на этапе i ,d(xi-1,xi) – кратчайшее расстояние от узла xi-1 до узла xi:
для алгоритма прямой прогонки
(4.1)
для алгоритма обратной прогонки
(4.2)
При i=1 полагаем f0(x0)=0.
Задача 1. Определите кратчайший маршрут между вершинами графа 1 и 10, представленного на рис. 4.1, с помощью метода динамического программирования. Для этого определите этапы и состояния системы с помощью прямой и обратной прогонки, представив данные в форме таблиц.
Рис. 4.1 – граф сети дорог к задаче 1
Рекуррентное уравнение для вычисления кратчайшего расстояния до узла xi на этапе i ,d(xi-1,xi) – кратчайшее расстояние от узла xi-1 до узла xi:
для алгоритма прямой прогонки
для алгоритма обратной прогонки
При i=1 полагаем f0(x0)=0.
Пример 2. Определите кратчайший маршрут между городами 1 и 7 на сети дорог, представленной на рис. 2 определите этапы и состояния системы с помощью обратной прогонки и решите задачу.
Рис. 4.2. - граф сети дорог к задаче 2
Пример 3. Определите кратчайший маршрут между вершинами графа 1 и 10, представленного на рис. 3. определите этапы и состояния системы с помощью обратной прогонки и решите задачу.
Рис.4.3 - граф сети дорог к задаче 3
Контрольные вопросы
Сформулируйте постановку задачи динамического программирования
Напишите рекуррентные уравнения для вычисления кратчайшего расстояния до узла xi на этапе i ,d(xi-1,xi) – кратчайшее расстояние от узла xi-1 до узла xi: