Контрольные вопросы

1. Сформулируйте постановку транспортной задачи линейного программирования.

2. Каковы отличия формулировки транспортной задачи от задачи линейного программирования в общей постановке.

3. Какие методы нахождения начального опорного плана транспортной задачи вы знаете?

4. Расскажите о методе потенциалов.

5. Дайте определение цикла пересчета.

6. Опишите решение транспортной задачи с помощью задачи, двойственной исходной.

7. Опишите алгоритм решения транспортной задачи с применением программной системы MATLAB.

8. Как проверить допустимость решения транспортной задачи?

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3

Темы: 3.1. Решение задач о назначениях

3.2. Решение задач дискретного программирования

Тема 3.1. Решение задач о назначениях

Теоретические сведения

Постановка задачи о назначениях: найти такую перестановку (р₁,р₂,..., р_n) из чисел 1,2,3,...,n, при которой обеспечен по всем перестановкам (р₁,р₂,..., р_n). Каждая такая перестановка может быть представлена точкой в п²- мерном евклидовом пространстве или в виде матрицы Х^п

Вводим переменные:

Х_ij = 1, если i-и механизм предназначен для j-й работы; х_ij = 0 — в противном случае.

Очевидно, что должно выполняться условие

(3.1)

Данные ограничения означают, что один механизм может быть предназначен для выполнения только одной работы. Тогда задача будет состоять в определении таких чисел {х_ij}, при которых достигается минимум функционала min при ограничениях (3.1).

Задачу о назначениях можно эффективно решить так же, как и транспортную задачу. Вместе с тем тот факт, что все величины спроса и предложения равны 1, привел к разработке упрощенного алгоритма решения, названного венгерским методом. Этот метод также основан на симплекс-методе.

Венгерский метод

.

Оптимальное решение данной задачи ЛП останется неизменным, если ко всем элементам какой-либо строки или столбца матрицы стоимостей ||c_ij|| прибавить константу или вычесть ее из этих элементов. Таким образом, стоимость c_ij изменится и будет равна

c_ij’ = c_ij-p_i-q_j (3.2)

Покажем, что при коэффициентах целевой функции c_ij’ получим те же оптимальные значения переменных x_ij , что и при коэффициентах c_ij.

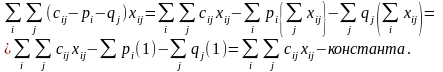(3.3)

Поскольку новая целевая функция отличается от исходной только на константу, оптимальные значения переменных x_ij должны быть одинаковы в обоих случаях. Таким образом показано, что этапы 1 и 2 венгерского метода, где p_i вычитаются из элементов строки I, а q_j – из элементов столбца j матрицы стоимостей, приводят к эквивалентной задаче о назначениях.

Основная идея венгерского метода заключается в переходе от исходной квадратной матрицы стоимости С к эквивалентной ей матрице Сэ с неотрицательными элементами и системой n независимых нулей, из которых никакие два не принадлежат одной и той же строке или одному и тому же столбцу. Для заданного n существует n! допустимых решений. Если в матрице назначения X расположить n единиц так, что в каждой строке и столбце находится только по одной единице, расставленных в соответствии с расположенными n независимыми нулями эквивалентной матрицы стоимости Сэ, то получим допустимые решения задачи о назначениях.

Следует иметь в виду, что для любого недопустимого назначения соответствующая ему стоимость условно полагается равной достаточно большому числу М в задачах на минимум. Если исходная матрица не является квадратной, то следует ввести дополнительно необходимое количество строк или столбцов, а их элементам присвоить значения, определяемые условиями задачи, возможно после редукции, а доминирующие альтернативы дорогие или дешевые исключить.

Задача 1. Решите задачи о назначениях, представленные в табл. 3.1.

а)

3	8	2	10	3
8	7	2	9	7
6	4	2	7	5
8	4	2	3	5
9	10	6	9	10

б)

3	9	2	3	7
6	1	5	6	6
9	4	7	10	3
2	5	4	2	1
9	6	2	4	5

в)

Дана следующая задача распределения четырех рабочих по четырем видам работ. Различная квалификация рабочих обусловливает различную стоимость выполнения работ. Стоимость работ приведена в табл. в). Отметим, что первый рабочий не может выполнять работу 3, а третий – работу 4. Найдите оптимальное решение.

50	50	-	20
70	40	20	30
90	30	50	-
70	20	60	70

г) Пусть в задаче из предыдущего упражнения можно ввести нового (пятого) рабочего, способного выполнять любой вид работ со стоимостью соответственно 60, 45, 30 и 80 у.е. Будет ли экономически выгодно заменить одного из работающих рабочих новым?

д) Пусть в задаче из предыдущего упражнения можно ввести новый вид работы, который может выполнить любой из четырех рабочих, со стоимостью соответственно 20, 10, 20 и 80 у.е. Будет ли новая работа более выгодной по сравнению с имеющимися?