Контрольные вопросы

1. Сформулируйте постановку задачи линейного программирования.

2. Каков геометрический смысл задачи линейного программирования.

3. Опишите решение задач линейного программирования графическим методом.

4. Что такое симплекс-метод?

5. Что такое симплекс-матрица?

6. Опишите решение задач линейного программирования симплекс-методом.

7. Что такое двойственные задачи линейного программирования?

8. Как проверить допустимость решения задачи линейного программирования.

Практическое занятие 2 Тема: Решение транспортных задач линейного программирования

Теоретические сведения

Под термином "транспортные задачи" понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов. В качестве критериев в транспортных задачах используют: критерий стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию), критерий времени (план оптимален, если на его реализацию затрачивается минимум времени) и другие.

Наиболее часто встречаются следующие задачи, относящиеся к транспортным:

• прикрепление потребителей ресурса к производителям;

• привязка пунктов отправления к пунктам назначения;

• взаимная привязка грузопотоков прямого и обратного направлений;

• отдельные задачи оптимальной загрузки промышленного оборудования;

• оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.

Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения. Имеются m пунктов отправления груза и объемы отправления по каждому пункту a₁, a₂ ,...,a_m . Известна потребность в грузах b₁, b₂ ,...,b_n по каждому из n пунктов назначения. Задана матрица стоимостей доставки по каждому варианту c_ij , . Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го пункта отправления (от поставщика) в каждый j-ый пункт назначения (до потребителя) x_ij с минимальными транспортными издержками.

В общем виде исходные данные представлены в табл. 2.1. Строки транспортной таблицы соответствуют пунктам отправления (в последней клетке каждой строки указан объем запаса продукта a_i ), а столбцы - пунктам назначения (последняя клетка каждого столбца содержит значение потребности b_j). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i-го пункта в j-й: в правом верхнем углу находится цена перевозки единицы продукта, а в левом нижнем - значение объема перевозимого груза для данных пунктов.

Таблица 2.1. Исходные данные

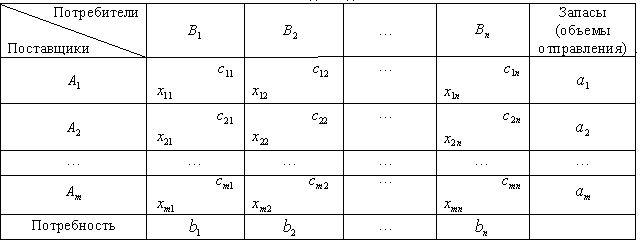
Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения

(2.1)

Если такого равенства нет (потребности выше запасов или наоборот), запасу называют открытой, т.е.:

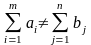
Для написания модели необходимо все условия (ограничения) и целевую функцию представить в виде математических уравнении.

Все грузы из i-х пунктов должны быть отправлены, т.е.:

(2.3)

Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:

(2.4)

Суммарные объемы отправления должны равняться суммарным объемам назначения (3.1). Должно выполняться условие неотрицательности переменных:

(2.5)

Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):

(2.6)

Вместо матрицы стоимостей перевозок (c_ij ) могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы. Как видно из выражения (7.1), уравнение баланса является обязательным условием решения транспортной задачи. Поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае, если

• потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления с объемом запасов. равным;

(2.7)

• запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления, равным:

(2.8)

Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.

Задача 1.

Производственные предприятия некоторой автомобильной фирмы расположены в городах A1, A2, A3. Основные центры продаж готовой продукции расположены в городах B1, B2. Объемы производства указанных предприятий равняются 1000, 1300 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах продаж составляют 2300 и 1400 автомобилей соответственно. Тарифы перевозки автомобилей по каждому из возможных маршрутов приведены в матрице C:

Найти оптимальный план переводок продукции, минимизирующий транспортные издержки.

Задача 2.

Фирма имеет производственные подразделения в местностях A1, A2, A3 , а также центры продаж готовой продукции в пунктах B1, B2, B3. производственные мощности подразделений равны 20, 20 и 30 единиц соответственно, а прогнозы спроса в центрах продаж – 10, 15 и 45 единиц соответственно. Транспортные издержки приведены в матрице С:

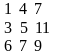
Найти оптимальный план переводок продукции, минимизирующий транспортные издержки.

Задача 3.

Производственное предприятие располагает тремя поставщиками сырьевых ресурсов для производства продукции: условно A1, A2, A3. Поставки из этих предприятий распределяются по пяти различным видам работ: условно B1, B2, B3, B4 и B5. От того, как будут распределены по этим видам работ объемы исходных материалов, зависит качество продукции. В качестве стоимостей в данном случае выступают стоимости бракованной продукции, получаемой при данном распределении сырьевых ресурсов по видам работ. Исходные количественные данные к задаче :

A₁=200, A₂=450, A₃=250; B₁=100, B₂=125, B₃=325, B₄=250, B₅=100.

Тарифы перевозки приведены в матрице С:

Найти оптимальный план переводок продукции, минимизирующий транспортные издержки.