Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Уфимский государственный авиационный технический университет»
Кафедра технической кибернетики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
ПО ДИСЦИПЛИНЕ
“Системный анализ, оптимизация и принятие решений”
для бакалавров по направлению
(код) 220100 «Системный анализ и управление»
(название)
(очной формы обучения)
Уфа 2012
СОДЕРЖАНИЕ
Введение 3
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1 4
Тема: решение задач линейного программирования симплекс-методом 4
Контрольные вопросы 6
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2 7
Тема: Решение транспортных задач линейного программирования 7
Контрольные вопросы 10
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3 11
Темы: 3.1. Решение задач о назначениях 11
3.2. Решение задач дискретного программирования 11
Тема 3.1. Решение задач о назначениях 11
Теоретические сведения 11
Контрольные вопросы 14
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4 15
Тема. Решение задач динамического программирования 15
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 5 17
Тема 1. Решение матричных игр 17
Теоретические сведения 17
Постановка задачи 17
Контрольные вопросы 20
Тема 2. Принятие решений в условиях неопределенности с применением математических игровых моделей 21
Контрольные вопросы 23
СПИСОК ЛИТЕРАТУРЫ 23
Введение
Целью практических занятий является закрепление лекционного материала, преподаваемого в 5 и 6 семестрах студентам, обучающимся по направлению 220100 «Системный анализ и управление» в рамках основного теоретического раздела курса “Системный анализ, оптимизация и принятие решений”.
В результате изучения данного курса обучающийся должен
знать:
- методы системного анализа и принятия решений в технических, экономических и социальных системах;
- методы системного анализа и принятия решений в технических, экономических и социальных системах;
уметь:
- принимать оптимальные или рациональные решения из множества альтернатив;
владеть:
- приемами разработки функционального программного обеспечения для проектируемых систем управления и принятия решений;
обладать следующими профессиональными компетенциями:
- применять аналитические, вычислительные и системно-аналитические методы для решения прикладных задач в области управления объектами техники, технологии, организационными системами, работать с традиционными носителями информации, распределенными базами знаний (ПК-1);
способность принимать научно-обоснованные решения на основе математики, физики, химии, информатики, экологии, методов системного анализа и теории управления, осуществлять постановку и выполнять эксперименты по проверке их корректности и эффективности (ПК-8);
способность применять методы системного анализа, технологии синтеза и управления для решения прикладных проектно-конструкторских задач (ПК-11.
В ходе практических занятий студенты должны самостоятельно решить ряд взаимосвязанных задач по оптимизации и принятию решений, используя теоретические знания, полученные при прослушивании лекций и изучении учебной литературы.
Каждое занятие рассчитано на 2 академических часа аудиторной работы студентов.
Практическое занятие 1 Тема: решение задач линейного программирования симплекс-методом
Теоретические сведения
Постановка данной задачи выглядит следующим образом.
Имеется множество переменных X = (x1, х2,..., хn). Целевая функция линейно зависит от управляемых параметров:
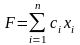(1.1)
Имеются ограничения, которые представляют собой линейные формы
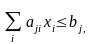где
.
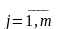(1.2)
Задача линейного программирования формулируется так:
Определить максимум линейной формы
F(x1,…,xn )=max(c1x1+…+cnxn) (1.3)
при условии, что точка (х1, х2,..., хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств
(1.4)
Любое множество значений (х1*, х2*,..., хn*), которое удовлетворяет системе неравенств (1.4) задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство
c1х1o+ c2 х2o+..+ cn хno ≥ c1х1+ c2 х2+..+ cn хn
для всего множества значений x1, х2,..., хn, то значение х1o..хno является оптимальным решением задачи линейного программирования.
В основе симплекс-метода лежит идея поиска базисного решения с последующим переходом от одного базиса к другому таким образом, чтобы целевая функция при этом все время увеличивалась, если речь идет о задаче максимизации. Для решения задачи линейного программирования нужно сформулировать постановку задачи в каноническом виде.
Переобозначим свободные коэффициенты ограничений aj0=bj. Приведем матрицу ограничений к каноническому виду:
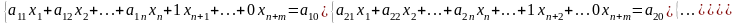(10.1)
Используя метод Жордана-Гаусса, приведем записанную систему к виду, где выделены базисные переменные. Введем условные обозначения:
x1, x2 , ... , xr - базисные переменные;
xr+1, xr+2 , ... , xn - свободные переменные.
Будем применять метод полного исключения к расширенной матрице ограничений. Выбираем направляющий элемент aij на данной итерации. В результате преобразования Гаусса получим новые значения коэффициентов:
(10.2)
Если l≠I, l=1,2,…,m.
Выясним условия,
при которых новое базисное решение
будет допустимым, т.е.
для всех l.
По предположению, al0≥0,
тогда
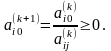
Если
то очевидно,
,
так как
,
Если
то
будет больше нуля при всех значениях
l=1,2,…,m
тогда и
только тогда, когда
при условии
Преобразование Гаусса называется симплексным преобразованием, когда направляющий элемент определяют по следующим правилам:
направляющий столбец выбирают из условия, что в нем имеется хотя бы один отрицательный элемент;
направляющую строку выбирают так, чтобы отношения
были минимальными при условии, что
aij>0.
Решение задачи линейного программирования с помощью симплекс-метода основано на представлении данных задачи в симплекс-таблице. Последовательность этапов решения задачи линейного программирования с применением симплекс-таблицы приведена в литературных источниках [1-3] и в конспекте лекций по данному курсу.
Задача 1.
Решить задачу линейного программирования симплекс-методом.
f(x) = 5x1 - 2x3 min
- 5x1 – x2 + 2x3 ≤ 2
- x1 + x3 + x4 ≤5
- 3x1 + 5x4 ≤7
xj ≥ 0, j = 1,2,3,4
Задача 2.
Найти максимум линейной формы 5х1 + 4х2 при ограничениях
6x1 + 4 х2≤24,
х1+2 х2≤6,
-х1+ х2≤1,
х2≤2,
х1≥0, х2≥0.
Сформулировать задачу, двойственную основной, решить задачу с применением MATLAB.
Задача 3.
Банк в течение нескольких месяцев планирует вложить до 200 000 долл. в кредитование частных лиц (клиентов) и покупок автомобилей. Банковские комиссионные составляют 14% при кредитовании частных лиц и 12% при кредитовании покупок автомобилей. Оба типа кредитов возвращаются в конце годичного периода кредитования. Известно, что около 3% клиентских и 2% автомобильных кредитов никогда не возвращаются. В этом банке объемы кредитов на покупку автомобилей обычно более чем в два раза превышают объемы других кредитов для частных лиц. Найдите оптимальное размещение средств по двум описанным видам кредитования и определите коэффициент возврата по всем кредитам.
Сформулировать задачу, решить с применением MATLAB.
Задача 4.
Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3 и S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, определены следующим образом:
f(x)=2x1 +3x2;
x1+3x2≤18;
2x1+x2≤16;
x2≤5;
3x1≤21;
Решить задачу симплекс-методом. Сформулировать задачу, двойственную основной, решить задачу с применением MATLAB.