2 Этап. Расчёт конического прямозубого редуктора
По (табл. 3.3 ; стр.34), принимаем: для шестерни сталь с твёрдостью НВ ; для колеса сталь с твёрдостью НВ
Допускаемые контактные напряжения [по формуле (3, 9)
= МПа
Здесь принято по (табл. 3.2) для колеса
σнlim b = 2НВ + 70 = МПА
При длительной эксплуатации коэффициент долговечности KHL =
Коэффициент безопасности примем [SH] =
Выбираем коэффициенты:
Коэффициент КНβ = (по табл. 3.1)
Коэффициент ширины венца ( по рекомендации ГОСТ 12289-76) принимаем равным ΨbRe=
Внешний делительный диаметр колеса
Для прямозубых Кd = 99, передаточное число u = up = ;
мм
Принимаем поГОСТ12289-76(стр. 49.) ближайшее стандартное значение de2 = мм
Примем число зубьев шестерни Z1 =
Число зубьев колеса Z2=Z1*Up=
Тогда Up=Z2/Z1=
Отклонения от заданного равно , что меньше установленного
Гост 12289-76 3%.
Внешний окружной модуль
me = de2/Z2 =
Углы делительных конусов
Ctgδ1 = u = ; δ1 =
δ2 = 90˚ - δ1 =
Внешнее конусное расстояние Re и длина зуба и
Re = 0, 5 me√z12 + z22 = мм
b = ΨBRE * Re = мм
Принимаем b =
de1 = me * Z1 = мм,
По ГОСТ 12289-76, округляем до мм,
d1 =2(Re – 0, 5b) sin δ1 = мм
Внешние диаметры шестерни и колеса (по вершинам зубьев)
dae1 = de1 + 2meCos δ1 = мм
dae2 = de2 + 2meCosδ1 = мм
Средний окружной модуль
m=d1/Z1 = мм
Коэффициент ширины шестерни по среднему диаметру
Ψbd = b/d1 =
Средняя окружная скорость колёс
v = ω2 * d1/2 = м/сек
Для конических передач обычно применяют 7-ю степень точности.
Для проверки контактных напряжений определяем коэффициент нагрузки.:
Кн = Кнβ*Кнα*Кнν
По (табл. 3.5) при Ψbd = , консольном расположением колёс и твёрдости НВ < 350 коэффициент учитывающий нагрузки по длине зуба,
Кнβ =
Коэффициент учитывающий распределение между прямыми зубьями
Кнα = (табл.3. 4)
Коэффициент учитывающий динамическую нагрузку в зацепление для прямозубых колёс при ,м/с Кнν = (табл. 3.6)
Кн =
П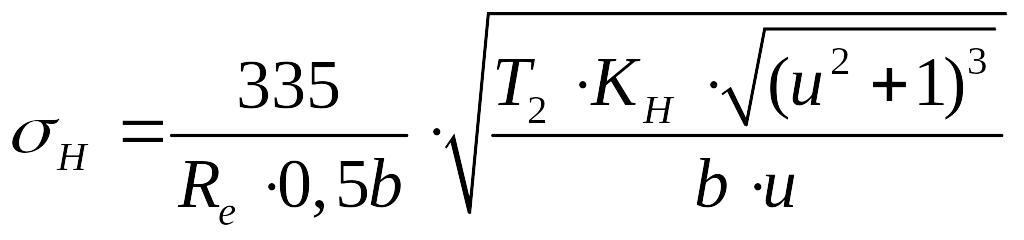
роверяем
контактное напряжение по формуле (3,27
)
Мпа
Силы в зацеплении :
окружная
Ft = 2T2/d1 = Н
радиальная для шестерни, равная осевой для колеса
Fr1 = Fa2 = Ft*tgα*cosδ = H
осевая для шестерни
Fa1 = Fr2 = Ft*tgα*sinδ1 = H
Проверка зубьев на выносливость по напряжениям изгиба [формула (3.3
σF = FtKFYF/эFbm=
Коэффициент нагрузки KF = KFβ * KFν
По (табл.3.7) при Ψbd = , несимметричном расположении колёс, валах на роликовых подшипниках и твердости , значения KFβ =
По (табл. 3.8) при твердости , скорости м/с и -й степени точности KFV =
Итак, KF = (стр. 43)
YF = коэффициент формы зуба выбираем от эквивалентных чисел зубьев, при Z= , YF= (стр.42)
для шестерни zV1 = z1/cos δ1 =
для колеса zV2 = z2/cosδ2 =
При этом YF1 = и YF2 =
Допускаемое напряжение при проверки зубьев на выносливость по напряжениям изгиба
[σF] = σ0Flim b/[SF]=
По (табл. 3.9) для стали 45 улучшенной при твёрдости НВ σ0Flim b = НВ.
Для шестерни σ0Flim b1 = МПА
Для колеса σ0Flim b2 = МПА
Коэффициент запаса прочности [SF] =[SF]’ * [SF]”. По (табл. 3.9) [SF]’ = , дл поковок и штамповок [SF]”=
[SF]’=
Допускаемые напряжения при расчёте зубьев на выносливость:
для шестерни [σF1] = МПА
для колеса [σF2] = МПА
для шестерни отношение [σF1]/YF1 = МПА
для колеса отношение [σF2]/YF2 = МПА
Дальнейший расчёт ведём для зубьев колеса, так как полученное отношение для него меньше
Проверяем зуб колеса:
σF2 = σF = FTKFYF/эFbm= =
= МПА<[σF]= МПа