25. Задача о тепловом импульс
,
,
.
,
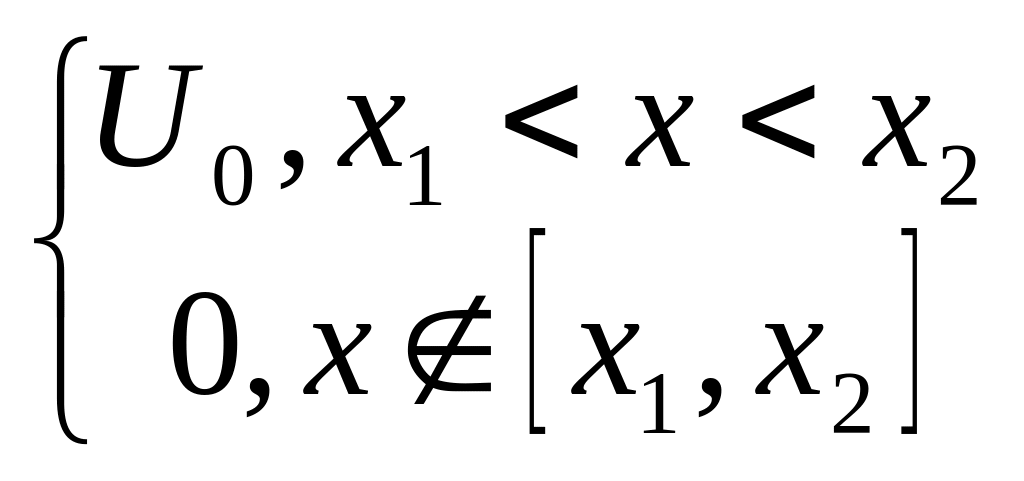или
,
Количество тепла
.
Решение задачи №2 легко можно получить
из решения задачи №1. Согласно (5) решение
задачи о тепловом импульсе имеет вид:
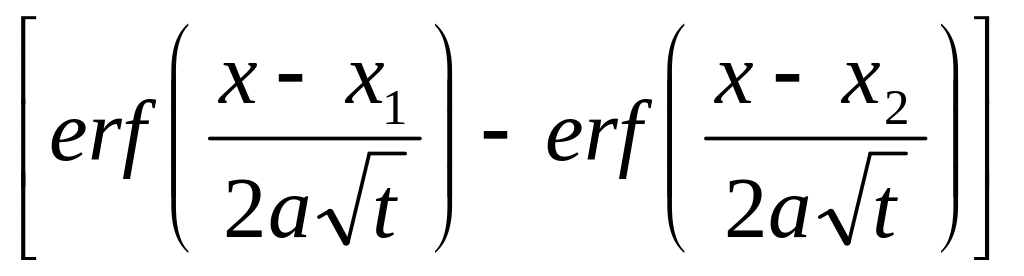(6).
26. Решение задачи Коши на бесконечной прямой
(1),
-
произвольная кусочно-непрерывная
прямая.
Для решение задачи (1), дается интеграл следующего вида:
(2), интеграл Пуассона
для теплопроводности. Дадим физическую
интерпретацию формулы (2) в физической
плоскости.
задает начальное распределение
температуры. Возьмем
(произвольную) выделим ей элементарный
участок
.
Предположим, что этому элементарному
участку соответствует мгновенный
точечный источник тепла
.
Тепло
,
а распределение температуры определяется
функцией Грина.
,
очевидно, что действие всех элементарных
источников распределенных по оси
определяется интегралом. Докажем
справедливость (2): Покажем, что функция
определяемая выражением (2) действительно
является решением задачи 1. кроме этого
необходимо показать сходимость интеграла
в (2), а т.же интегралов вида:
,
,
.
Решение определен-ном (2) подставим в
задачу 1:
/по
определению функции Грина это
функция/
/по
свойству
функции/
,
подставим в само уравнение:
,
функция Грина является решением уравнения
теплопроводности
.
Доказательство сходимости интегралов
рассмотрим в предположение, что
ограничена не которым значением
в формуле (2).
.
жно
получить из решения зния теплопроводности
(1)
/
/
.
Докажем, что
и это интеграл
сходиться.
/
/
,
оба интеграла сходятся. Сходимость
,
доказывается аналогично сходимости
производной от интеграла по
.
отсюда следует сходимость интеграла
Пуассона (2) обладает 3-мя следствиями:
Следствие 1. Скорость распространения тепла бесконечна (это свойство решения всех уравнений параболического типа).
Следствие 2. Если
функция
четная
,
тогда
.
Следствие 3. Если функция не четная .
27. Решение неоднородного уравнения теплопроводности
на бесконечной прямой.
(1) , где функция
- функция плотности тепловых источников,
она непрерывна, ограничена.
Решение задачи
(1) найдем в виде:
(2), где функция
является решением задачи:
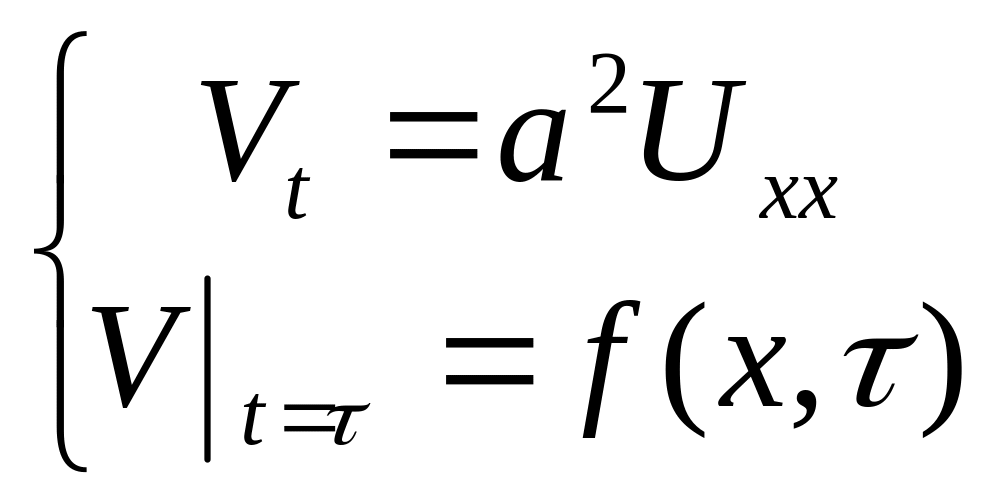(3), где
- параметр.
Решение задачи (3) дается в виде интеграла Пуассона:
,
решение задачи (1) имеет вид:
(4). Докажем (4):
.
,
т.к
,
т.к
- решение однородности.
28. Функция Грина для однородных гу 1 и 2 рода
Граничные условия первого рода (однородные)
(1).
Для решения (1) воспользуемся следствием 3 из интеграла Пуассона. Для этого функцию продолжим нечетным образом по отрицательной части, прямой. - можно записать интеграл Пуассона:
-
/
/
(
)
,
в (…)
,
- функция Грина 1-ой краевой задачи.
(
-
);
-
.
Решение задачи
(1):
(2). Рассмотрим задачу: имеется стержень,
температура стержня =
,
боковая поверхность теплоизолирована.
Температура на левой границе =0. Подставим
значение
.
-
)
/
/
(
)
.
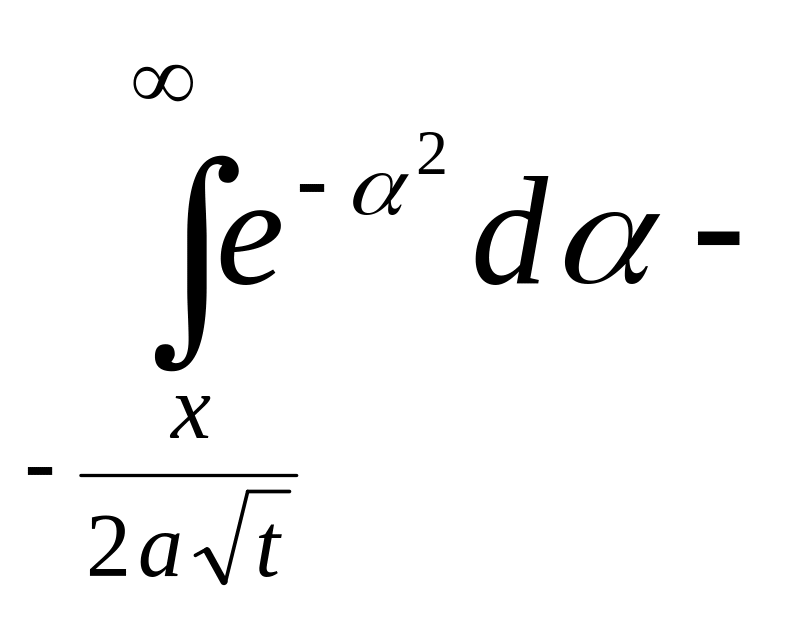
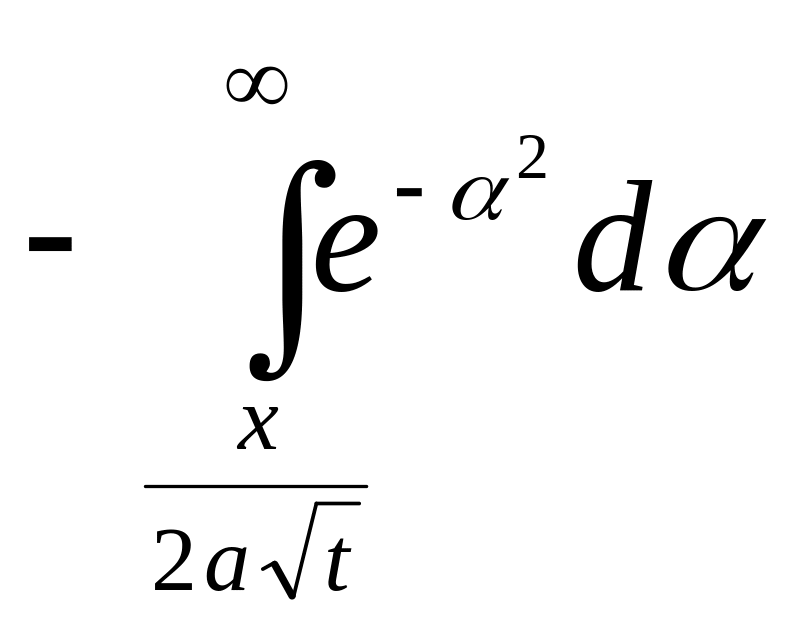Граничные условия второго рода (однородные)
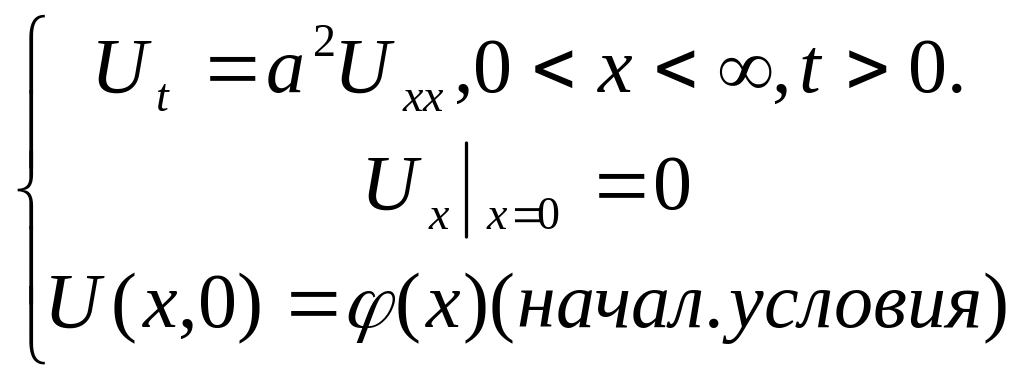(1)
- поток тепла =0, т.е тепло не переходит,
адиабатическое. Для решения задачи (1)
функцию
продолжим четным образом.
по следствию 2 производная
на
границе =0. воспользуемся интегралом
Пуассона на
прямой:
(
)
,
т.к
.
В (…)
(
+
)
+
.
Рассмотрим физическую задачу: имеется полуограниченный стержень, боковая поверхность полуизолированная.
.