1.5. Оптимизационные задачи в экономическом моделировании
Анализ деятельности финансового учреждения, промышленного предприятия или коммерческой фирмы, который проводит студент в дипломной работе, связан с поиском управленческих решений относительно оптимального размещения производственных заказов, рационального использования ресурсов, формирования портфеля ценных бумаг и т.п. Поиск наиболее приемлемого варианта управленческого решения - это задача оптимизации. Сущность ее состоит в определении таких параметров функционирования объекта управления Хj , которые при наличии определенных ограничений обеспечивали бы достижение заданного значения целевой функции Z(х). Целевая функция чаще всего экстремальна: это максимальная прибыль, минимальные расходы и т.п.
Например, математические модели некоторых задач оптимизации имеют вид:
- задача на максимум прибыли:
(3)
- задача на минимум расходов:
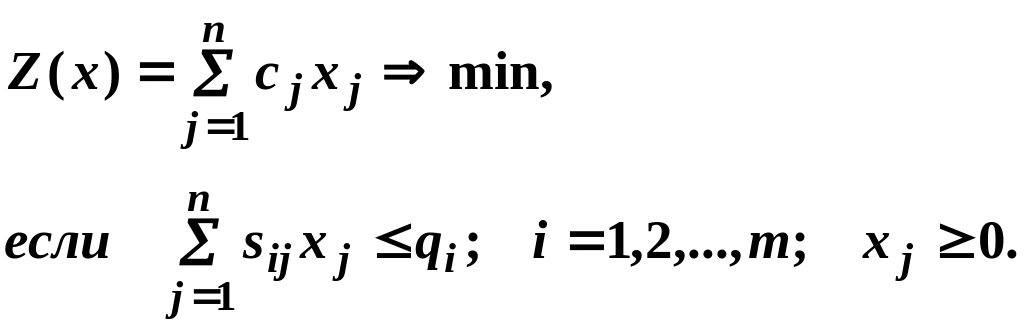(4)
В
приведенных формулах приняты следующие
обозначения:
-
объем
производства
-го
вида
продукции,
- прибыль
от реализации единицы
-
го
вида
продукции,
- себестоимость производства единицы
-
го
вида
продукции,
- ресурсоемкость
( материалоемкость,
энергоемкость)
единицы
-
го
вида
продукции;
- запасы ресурсов.
Для решения такого типа оптимизационных задач в среде Ехсеl используют инструменты надстройки Поиск решения (Сервис => Поиск решения. См.рис 15).
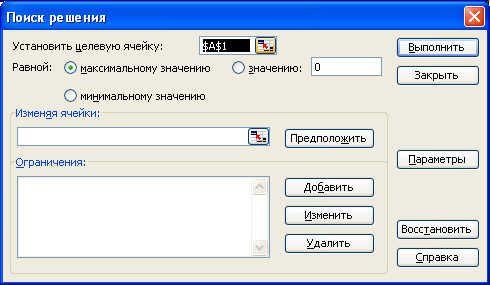
Рис. 15. Окно Поиск решения
Это мощное аналитическое средство, которое позволяет работать с большим количеством ограничений, определяет оптимальное (для указанных условий – ограничений) решение.
Поиск решений является частью блока задач, который иногда называют Анализ «что-если». Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках при заданных в модели ограничениях. Эти ограничения могут ссылаться на другие влияющие ячейки.
Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму целевой ячейки — например, можно изменить объем планируемого бюджета рекламы и увидеть, как это повлияет на проектируемую сумму расходов.
В составе Microsoft Excel в папке Office\Samples находится книга с примерами (Solvsamp.xls) использования процедуры поиска решения (Solver.xls).
Примеры, содержащиеся в книге Solvsamp.xls, могут быть трансформированы в задачи, поставленные в аналитической части дипломной работы. Чтобы применить любой из шести примеров: «Структура производства», «Транспортная задача», «График занятости», «Управление капиталом», «Портфель ценных бумаг» и «Проектирование цепи», — откройте книгу, перейдите к нужному листу и выберите команду Поиск решения в меню Сервис.
Ниже приведен пример транспортной задачи:
-
Пример 2: Задача перевозки грузов.
Требуется минимизировать затраты на перевозку товаров от предприятий-производителей
на торговые склады. При этом необходимо учесть возможности поставок каждого из произ-
водителей при максимальном удовлетворении запросов потребителей.
Число перевозок от завода x к складу y:
Заводы:
Всего
Казань
Рига
Воронеж
Курск
Москва
Беларусь
5
1
1
1
1
1
Урал
5
1
1
1
1
1
Украина
5
1
1
1
1
1
---
---
---
---
---
Итого:
3
3
3
3
3
Потребности складов -->
180
80
200
160
220
Заводы:
Поставки
Затраты на перевозку от завода x к складу y:
Беларусь
310
10
8
6
5
4
Урал
260
6
5
4
3
6
Украина
280
3
4
5
5
9
Перевозка:
83р.
19р.
17р.
15р.
13р.
19р.
В этой модели представлена задача доставки товаров с трех заводов на пять региональных складов
Товары могут доставляться с любого завода на любой склад, однако, очевидно, что стоимость
доставки на большее расстояние будет большей. Требуется определить объемы перевозок между
каждым заводом и складом, в соответствии с потребностями складов и производственными
заводов, при которых транспортные расходы минимальны.
В примерах уже подобраны целевая и влияющие ячейки, а также ограничения.
Предлагаемые примеры могут быть отредактированы под конкретную оптимизационную задачу.