Двухвыборочный f-тест для дисперсий.

F-тест в однофакторном дисперсионном анализе устанавливает, значимо ли различаются средние нескольких независимых выборок. Он заменяет t-тест для независимых выборок при наличии более двух выборок и дает тот же результат в случае двух выборок. F-тест является односторонним, т.е. гипотеза о неравенстве средних принимается, если расчетное значение критерия меньше критического, найденного по распределению Фишера.

Корреляционный анализ.

До сих пор речь шла главным образом о таких статистических характеристиках, как среднее значение и отклонение, которых обычно достаточно при работе с одномерными данными (например, только с заработной платой служащих). Однако на практике существует достаточно большое количество явных и неявных взаимосвязей, например, между той же заработной платой служащего и его образованием, объемом выпускаемой продукции и затратами на производство, между объемом сбыта и уровнем дохода, между производительностью работников и их отношением к труду и т.д. Иначе говоря, на практике речь часто может идти о двумерных данных и зависимостях между ними.

Существует два базовых инструмента, с помощью которых анализируются двумерные данные (например, зарплата и образование): корреляционный анализ, позволяющий оценить степень взаимосвязи между двумя факторами (если такая взаимосвязь вообще существует), и регрессионный анализ, который показывает, как можно предсказать поведение одной из двух переменных или управлять ею с помощью другой.

Microsoft Excel располагает двумя функциями КОРРЕЛ (или ПИРСОН), которые предназначены для расчета генерального и выборочного коэффициента корреляции между двумя переменными. В результате выдается таблица (корреляционная матрица), показывающая значение функции КОРРЕЛ (или ПИРСОН) для каждой возможной пары переменных измерений.

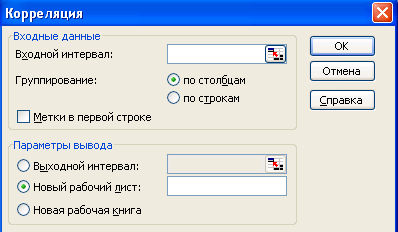
Рис. 11. Окно Корреляция

В отличие от ковариационного анализа коэффициент корреляции масштабируется таким образом, что его значение не зависит от единиц, в которых выражены переменные двух измерений (например, если вес и высота являются двумя измерениями, значение коэффициента корреляции не изменится после перевода веса из фунтов в килограммы). Любое значение коэффициента корреляции должно находится в диапазоне от -1 до +1 включительно.

Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть, большим значениям одной переменной соответствуют большие значения другой переменной (положительная корреляция), или, наоборот, меньшим значениям одной переменной соответствуют большие значения другой (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).

Пример: имеются данные о росте брака в производстве изделия А и количестве аттестованной продукции (таблица 3). Следует установить, существует ли взаимосвязь между ростом брака и количеством аттестованной продукции.

Таблица1.3

Данные выборки по браку изделий

Рост брака (%)	К-во изделий
1	25
2	20
3	15
4	10
5	5

Введем данные в лист Microsoft Excel:

Вызовем функцию Корреляция. На листе результатов получим:

	Столбец 1	Столбец 2
Столбец 1	1
Столбец 2	-1	1

Результаты говорят о наличии отрицательной корреляции между показателями (с коэффициентом –1, что позволяет сделать вывод о функциональной (линейной) связи между показателями).

Заметим, что для проверки взаимосвязи между данными есть функция ковариация, но следует учитывать, что ее значения зависят от размерности данных.

Двухмерная статистическая зависимость может быть наглядно представлена диаграммой рассеивания, используя Мастер диаграмм. На этой диаграмме представлена информация как о каждой отдельной переменной, так и о существующей между ними связи.