Дисперсионный анализ.

Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на изучаемый признак. В зависимости от количества факторов, включенных в анализ, различают однофакторный, двухфакторный и многофакторный анализ. Требуемый вариант выбирается в зависимости от поставленной задачи.

Однофакторный дисперсионный анализ. Используется в тех случаях, когда есть несколько независимых выборок, полученных из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений (например, этот фактор - тип упаковки). Для полученных выборок предполагается, что они имеют различные выборочные средние и одинаковые выборочные дисперсии. Поэтому необходимо ответить на вопрос, оказал ли изменяемый независимый фактор существенное влияние на разброс выборочных средних результативного признака или же разброс является следствием случайностей, вызванных небольшими объемами выборок. Другими словами, если выборки принадлежат одной генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп). При требованиях:

а) наблюдения независимы и проводятся в одинаковых условиях;

б) все совокупности нормально распределены;

в) дисперсии всех совокупностей равны;

проверяется гипотеза о равенстве средних значений выборок при заданном уровне значимости Alpha (как правило, равном 0,05) по критерию Фишера. Если расчетное значение критерия Фишера будет меньше критического (табличного), то гипотеза о равенстве средних выборочных принимается, т.е. нет оснований считать, что независимый фактор оказывает существенное влияние на разброс средних значений. В противном случае независимый фактор оказывает существенное влияние на разброс средних значений и гипотеза отвергается.

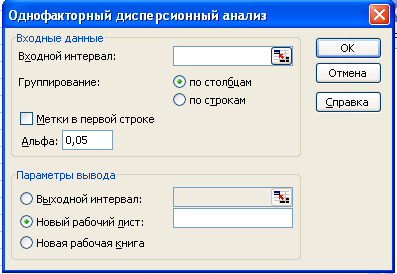
Рис. 10. Окно однофакторного дисперсионного анализа

Двухфакторный дисперсионный анализ с повторениями. Этот вид анализа применяется, если на результативный признак одновременно влияет два фактора, причем для каждого фактора может быть несколько выборок его уровней. Например, в опыте по измерению роста (результативный признак) растения обрабатывали удобрениями различных производителей (например, А, В, С) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура} имеется набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:

1. извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности независимо от температуры (шаг 1);

2. извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности независимо от марки удобрения (шаг 2);

3. извлечены ли 6 выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений и уровней температуры, из одной генеральной совокупности (шаг 3). Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.

Двухфакторный дисперсионный анализ без повторения. Этот вид анализа полезен при классификации данных по двум измерениям, как и двухфакторный дисперсионный анализ с повторением. Однако при этом анализе предполагается только по одной выборке уровней факторов (например, для каждой пары {удобрение, температура} в примере выше). При этом анализе можно добавлять проверки в шаги 1 и 2 двухфакторного дисперсионного анализа с повторениями, но недостаточно данных для добавления проверок в шаг 3.