3. Задача 18.2.

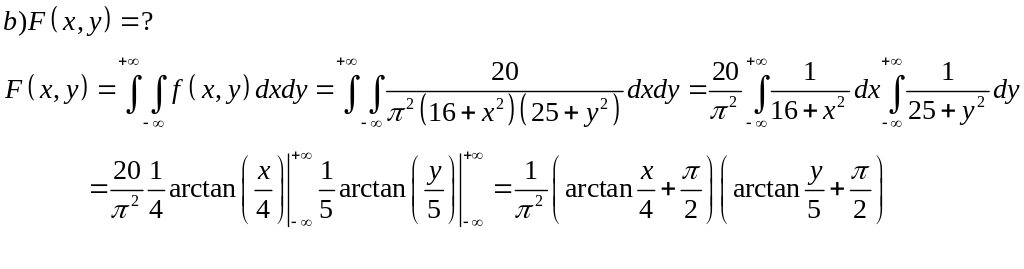
Экзаменационный Билет №20

1.Правило 3-х сигм.

Пусть имеется нормально распределённая случайная величина  с математическим ожиданием, равным а и дисперсией ².

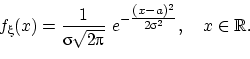
Определим вероятность попадания  в интервал (а – 3; а + 3), то есть вероятность того, что  принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.

_{P(а – 3<  < а + 3)=Ф(3) – Ф(–3)=2Ф(3)}

По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практически равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3.

2. Числовые характеристики системы 2-х случайных величин.

Начальным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения Х^k на Y^s:

α_{k, s}=M[X^kY^s]

Центральным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин:

µ_{k, s}=

где,

Для прерывных случайных величин:

,

где p_ij = P((X=x_i)(Y=y_j)) - вероятность того, что система (X, Y) примет значения (x_i, y_j), а суммирование распространяется по всем возможным значениям случайных величин X, Y.

Для непрерывных случайных величин:

Mатематические ожидания величин X и У, входящих в систему:

m_x= α_1,0 = M[X¹Y⁰] = M[X]

m_x= α_0,1 = M[X⁰Y¹] = M[Y]

Дисперсии величин X и У: D_x = µ_{2, 0}= =

D_y = µ_{0, 2}= =

Характеристика К_xy называется корреляционным моментом:

Для прерывных случайных величин:

Для непрерывных случайных величин:

Для независимых случайных величин корреляционный момент равен нулю.

Характеристика называется коэффициентом корреляции величин X и Y:

, где - средние квадратические отклонения величин X, Y.

Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать по линейному закону. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами.

Если случайные величины X а У связаны точной линейной функциональной зависимостью: Y=aX+b, то | | = 1.

3.Задача 6.7.

Экзаменационный Билет №21

1. Системы случайных величин. Закон распределения, функция распределения.

Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами.

Результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами.

Закон распределения:

F(x,y)=P((X<x)(Y<y))= .

F(x,+∞)=F₁(x) , F(+∞, y)=F₂(y)

Функция распределения системы двух случайных величин:

Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х<х и У<у: F(x,y)=P((X<x)(Y<y)).

Функцией распределения системы n случайных величин (X₁,Х₂, ..., Х_n) называется вероятность совместного выполнения n неравенств вида X_i < x_i:

F(x₁,x₂,…,x_n)=P((X₁<x₁) (X₂<x₂)… (X_n<x_n))

Свойства функции распределения системы случайных величин:

• Функция распределения F(x, у) есть неубывающая функция обоих своих аргументов, т.е. при и

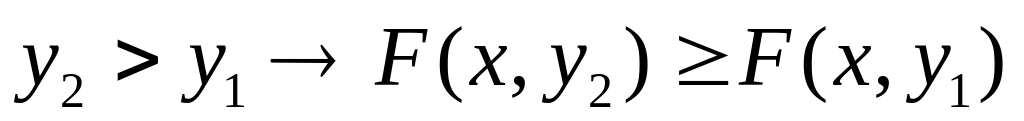
• Повсюду на -∞ функция распределения равна нулю: F(-∞,y)=F(x,-∞)=0.

• При одном из аргументов, равном +∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:

• F(x,+∞)=F₁(x) , F(+∞, y)=F₂(y), где F₁(x), F₂(y) — соответственно функции распределения случайных величин X и Y.

• Если оба аргумента равны +∞, функция распределения системы равна единице: F(+∞,+∞)=1.

2 .Зависимые и независимые случайные величины .

Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины X и Y называются зависимыми.

Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.

Задача 5.10.

Для не совместных событий

Экзаменационный Билет №22

1.Плотность распределения системы 2-х случайных величин, плотность распределения отдельных величин, входящих в систему.

Функция называется плотностью распределения системы.

Выражение для плотности распределения величины X:

F₁(x) = F(x,∞)

Аналогично: F₂(y) = F(∞,y)

2.Неравенство Чебышева.

a. Первая формула.

Если х – случайная неотрицательная велична, то

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

2. Для непрерывных величин

b. Вторая формула.

Пусть имеется случайная величина X с математическим ожиданием m_x и дисперсией D_x. Неравенство Чебышева утверждает, что каково бы ни было положительное число а, вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на , ограничена сверху величиной : .

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

2. Для непрерывных величин

Примечание.

Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина X выйдет за пределы участка значительно меньше ¹/₉