3.Задача 7.3.

Экзаменационный Билет №18

1. Нормальное распределение случайных величин, его характеристики.

Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, σ. Плотность распределения величины X равна:

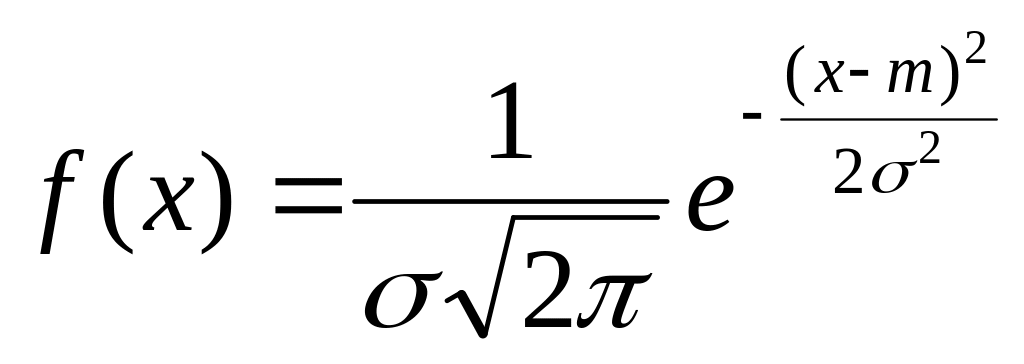
Математическое ожидание: m_x=m, а дисперсия D_x=σ².

Отсюда находим функцию распределения:

Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению σ:

Пользуясь мерой точности h, можно записать нормальный закон в виде:

2.Теоремы о числовых характеристиках:

1- Математическое ожидание неслучайной величины

Если с — неслучайная величина, то

2- Если с — неслучайная величина, то

3- Если с — неслучайная величина, а X — случайная, то

т. е. неслучайную величину можно выносить за знак мате матического ожидания.

Доказательство.

а) Для прерывных величин

б) Для непрерывных величин

4- Если с — неслучайная величина, а X — случайная, то

т. е. неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат.

Доказательство.

По определению дисперсии

Следствие т. е. неслучайную величину можно выносить за знак среднего квадратического отклонения ее абсолютным значением.

5- математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

Доказательство.

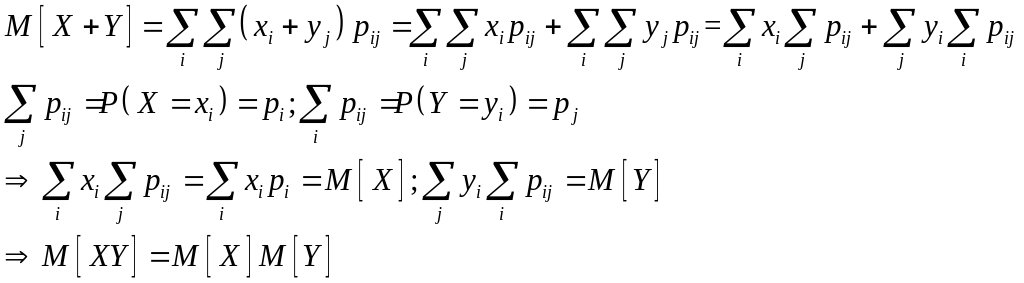
Задача 7.8.

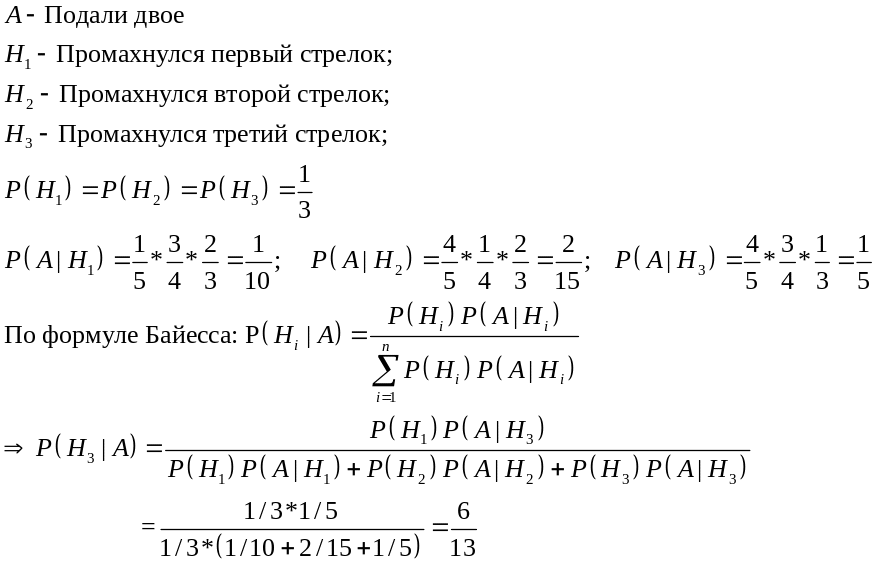
Экзаменационный Билет №19

1.Интеграл вероятности, его применение для вычисления вероятности попадания на заданный интервал.

Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, σ. Плотность распределения величины X равна:

Математическое ожидание: m_x=m, а дисперсия D_x=σ².

Отсюда находим функцию распределения: F(x) =

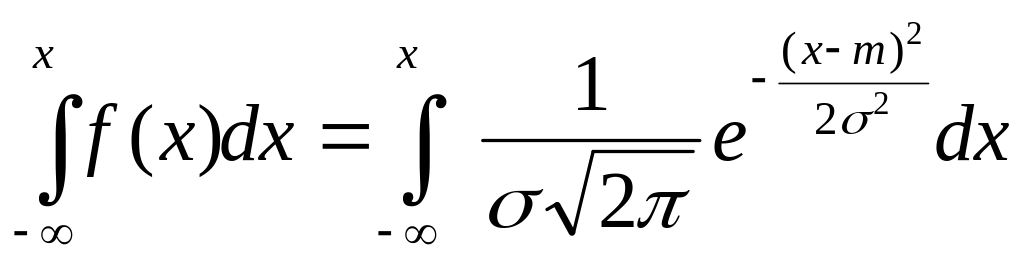
Сделаем замену переменной: и приведем его к виду: F(x) =

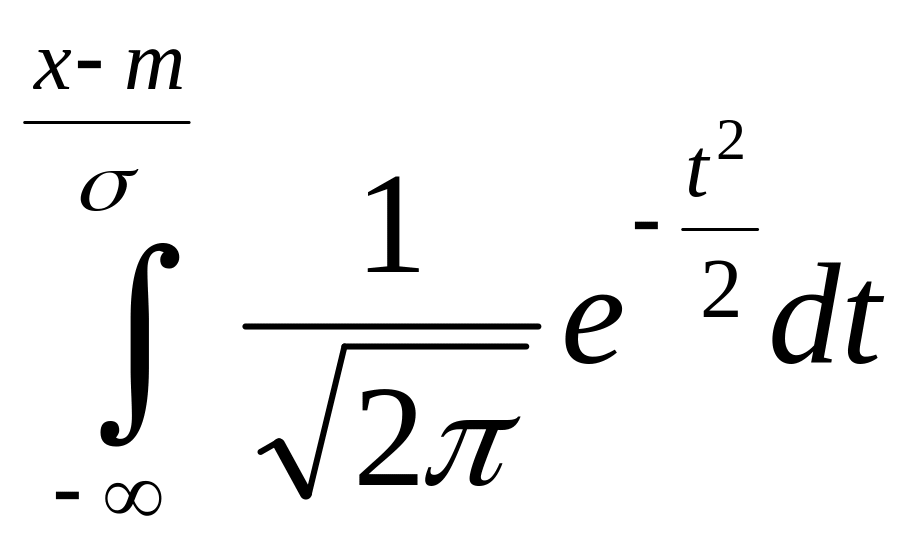
Интеграл не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения или (так называемый интеграл вероятностей), для которого составлены таблицы.

Условимся называть функцию нормальной функцией распределения.

Выразим функцию распределения величины X с параметрами m и σ через нормальную функцию распределения:

Теперь найдем вероятность попадания случайной величины X на участок от α до β. Согласно формуле:

2 Числовые характеристики функции случайных величин.

1- Если X — дискретная случайная величина с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

а величина У связана с X функциональной зависимостью то матическое ожидание величины У равно

а дисперсия выражается любой из двух формул

Если (X, Y) — система дискретных случайных величин, распределение которой характеризуется вероятностями , a то математическое ожидание величины Z равно

а дисперсия выражается любой из двух формул

2- Если X — непрерывная случайная величина с плотностью распределения , а , то математическое ожидание величины У равно

а дисперсия выражается любой из двух формул

Если (X, У) — система непрерывных случайных величин с плотностью , a , то математическое ожидание величины Z равно

а дисперсия выражается любой из двух формул

Если — система п непрерывных случайных величин с плотностью а , то