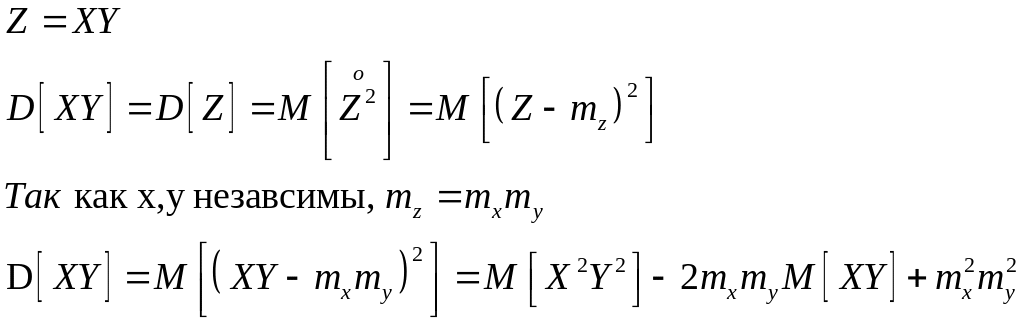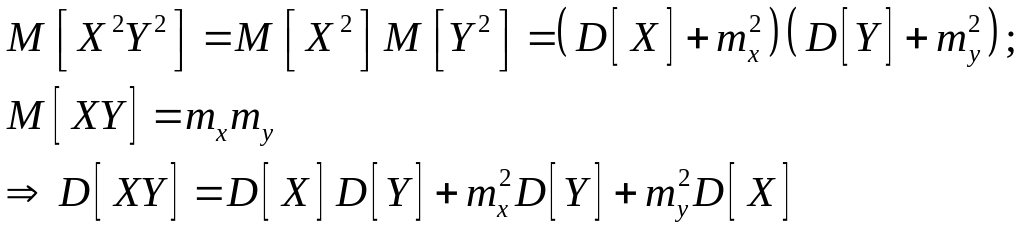2.Корреляционная функция случайных функций, ее свойства. Взаимная корреляционная функция.

Корреляционной функцией случайной функции X(t) называется неслучайная функция двух аргументов , которая при каждой паре значений t, t’ равна корреляционному моменту соответствующих сечений случайной функции:

Где — центрированная случайная функция.

При t' = t корреляционная функция превращается в дисперсию случайной функции:

Основные свойства корреляционной функции:

1) Cимметричность т.е. функция не меняется при замене t на t’

2)

3) Функция — положительно определенная, т.е.

где — любая функция; (В) — любая область интегрирования, одинаковая для обоих аргументов.

Взаимной корреляционной функцией двух случайных функций X(t) и У(t) называется неслучайная функция двух аргументов X и У, которая при каждой паре значений t, t' равна корреляционному моменту соответствующих сечений случайной функции X(t) и случайной функции У

Взаимная корреляционная функция, так же как и обычная корреляционная функция, не изменяется при прибавлении к случайным функциям любых неслучайных слагаемых, а следовательно, и при центрировании случайных функций.

Из определения взаимной корреляционной функции вытекает, что

Нормированной взаимной корреляционной функцией двух случайных функций X(t), Y(t) называется функция

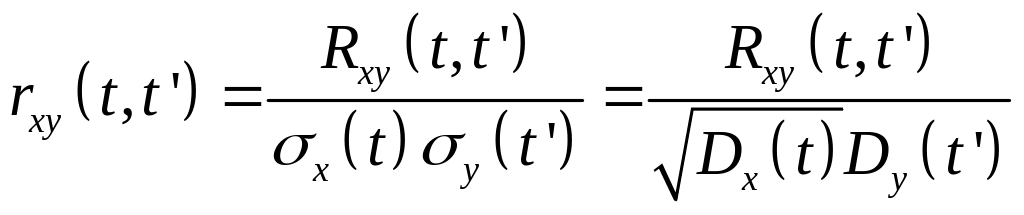
Случайные функции X(t) и Y(t) называются некоррелированными, если

Ecли Z(t) = X(t) + Y(t), тo

Для некоррелированных случайных функций X(t) и У(t)

3. Задача 8.4

Экзаменационный Билет №15

1.Распределение Пуассона, его числовые характеристики.

Cлучайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой:

где — некоторая положительная величина, называемая параметром закона Пуассона.

Параметр представляет собой не что иное, как математическое ожидание случайной величины X.

Дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию .

Законом Пауссона может быть приближенно заменно биномиальное распределение, когда вероятность р попадания события А в каждом отдельном опыте мала, а число n производимых опытов велико.

2. Характеристики случайных функций:

Математическим ожиданием случайной функции X(t) называется неслучайная функция которая при каждом t представляет собой математическое ожидание соответствующего сечения случайной функции:

Здесь p(x,t) — одномерная плотность распределения случайной величины х в соответствующем сечении случайного процесса X(t).

Дисперсией случайной функции X(t) называется неслучайная функция ,значение которой для каждого момента времени равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно m_x(t).

3.Задача 8.6.

Экзаменационный Билет №16

1.Равномерное распределение, его характеристики.

Н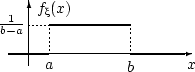 епрерывная случайная величина имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.

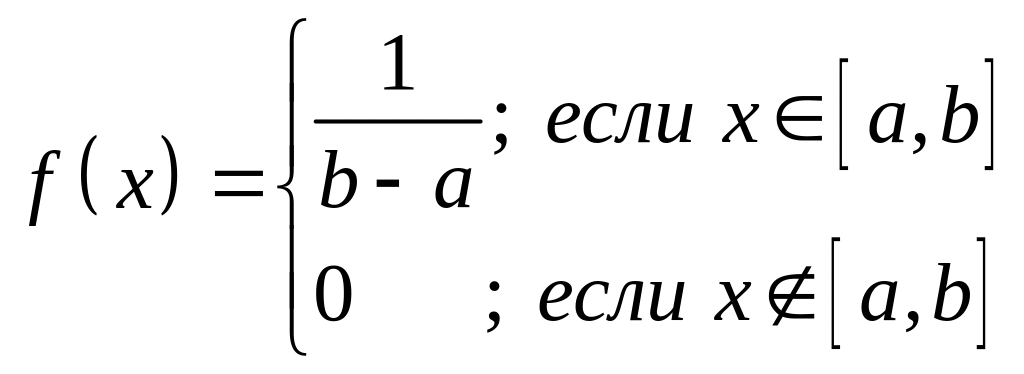
Очевидно, что площадь под графиком этой функции равна единице и . Поэтому является плотностью распределения.

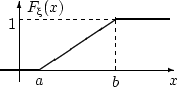Ф ункция распределения случайной величины Х:

Математическое ожидание

Дисперция

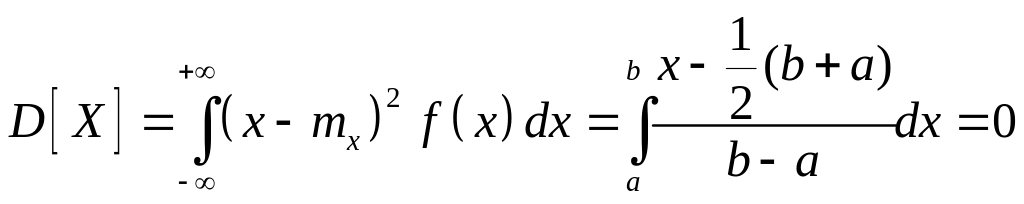
2.Понятие случайной функции. Закон распределения случайной функции, плотность распределения случайной функции.

Случайной функцией X(t) называется функция, которая в результате опыта может принять тот или иной конкретный вид, неизвестно заранее, какой именно.

Конкретный вид, принимаемый случайной функцией в результате опыта, называется реализацией случайной функции.

При фиксированном t случайная функция X(t) обращается в случайную величину X(t), называемую сечением случайной функции.

О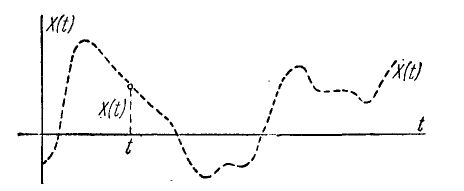 дномерным законом распределения случайной функции X(t) называется закон распределения f(x, t) сечения X(t) случайной функции.

Двумерным законом распределения случайной функции X(t) называется закон распределения системы двух ее сечений: X(t₁), Х(t₂), представляющий собой функцию четырех аргументов:

Случайная функция X(t) называется нормальной, если закон распределения системы любого числа n ее сечений представляет собой п-мерный нормальный закон.

3. Задача 8.9.

Экзаменационный Билет №17

1.Показательное ( экспоненциальное ) распределение, его числовые характеристики.

имеет показательное (экспоненциальное) распределение с параметром , и пишут: , если имеет следующую плотность распределения:

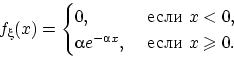
Функция распределения случайной величины непрерывна:

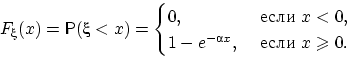
Для случайной величины Т, распределенной по показательному закону m_t=1/α; D_t=1/α².

2. Теоремы о числовых характеристиках: , , , .

1- Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент:

Доказательство.

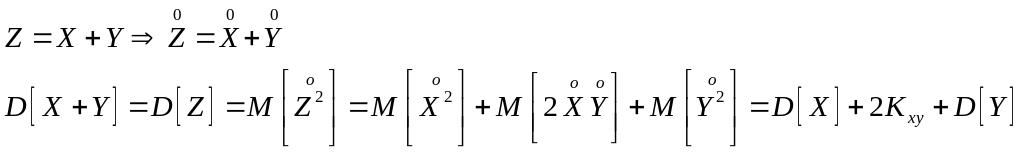
2- Дисперсия линейной функции:

где К_ij — корреляционный момент величин Х_i, X_j.

Доказательство.

Введем обозначение: Тогда

где — корреляционный момент величин

Вычислим этот момент. Имеем:

Подставляя это выражение в (1), приходим к формуле

В частном случае, когда все величины (X₁ X₂, .... Х_n) некоррелированны, то дисперсия линейной функции некоррелированных случайных величин равна сумме произведений квадратов коэффициентов на дисперсии соответствующих аргументов.

3- Математическое ожидание произведения случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

Доказательство.

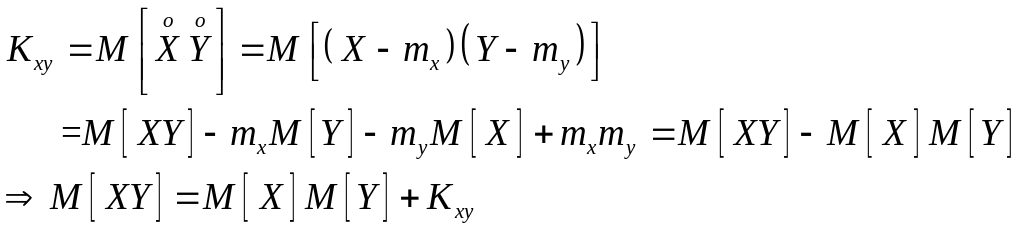
Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

4- Дисперсия произведения независимых случайных величин:

Доказательство.