Экзаменационный Билет №12

1.Числовые характеристики случайных величин. Характеристики положения.

Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает слсоотную величину с вероятностной точки зрения.

Однако во многих вопросах практики нет необходимости характеризовать случайную величину полностью, исчерпывающим образом. Зачастую достаточно бывает указать только отдельные числовые параметры, до некоторой степени характеризующие существенные черты распределения случайной величины. Такие характеристики, назначение которых — выразить в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.

1- Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

— для дискретной случайной величины;

— для непрерывной случайной величины.

– Для смешанной случайной величины, где сумма распространяется на все точки разрыва функции распределения, а интеграл — на все участки ее непрерывности.

2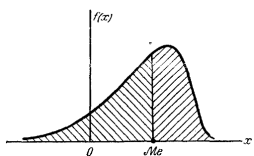 - Модой случайной величины называется ее наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины: модой является то значение, в котором плотность вероятности максимальна.

3- Медианой случайной величины X называется такое ее значение , для которого ,т. е. одинаково вероятно, окажется ли случайная величина меньше или больше

2.Закон больших чисел.

Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным. К ним относятся теоремы Чебышева и Бернулли

Математическая формулировка:

Последовательность случайных величин ... и

Если находит последовательность постоянных величин, что для любого

то такая последовательность случайных величин подчиняет закон больщих чисел.

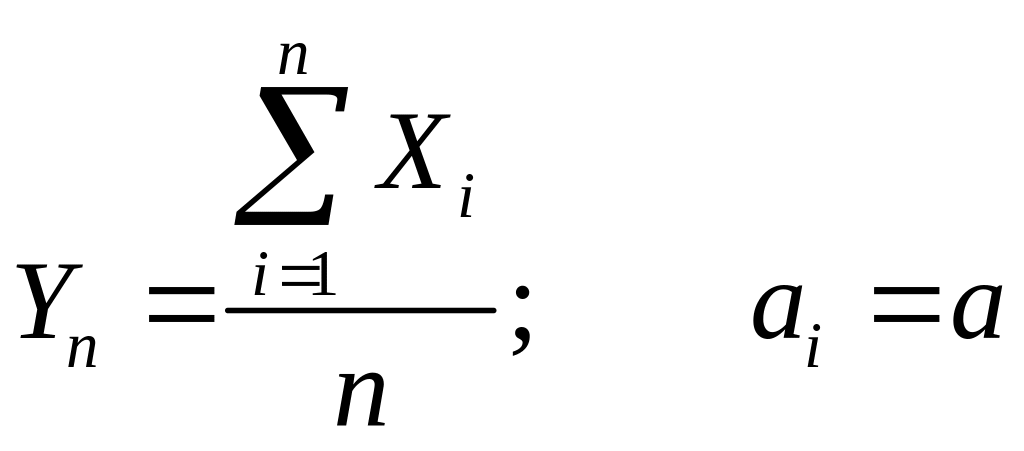
Теорема Чебышева

Пусть папарны независимых случайных величин, имеющих математическое ожидание М[X­_i] и дисперцию, ограниченную некоторую постоянную величину с, .

При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.

Теорема Бернулли

Если m число появления события А в n независимых испытаниях с вероятностью успеха в одном испытании p, , то для любого  справедливо .

3. Задача 12.10.

X – событие: выпускается бракованное изделие

Xi	1	2	…	k
Pi	p	qp	…	qk-1p

Где q = 1 – p

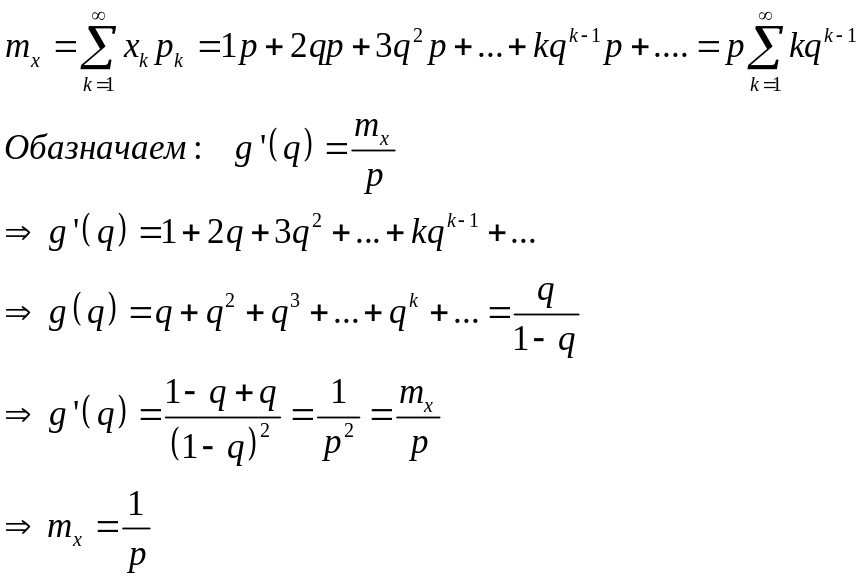
Экзаменационный Билет №13

1.Числовые характеристики случайных величин. Моменты. Характеристики рассеивания.

1- Моменты

Начальным моментом k-го порядка случайной величины X называется математическое ожидание к-й степени этой случайной величины:

Для дискретной, непрерывной и смешанной случайной величины вычисляется соответственно по формулам:

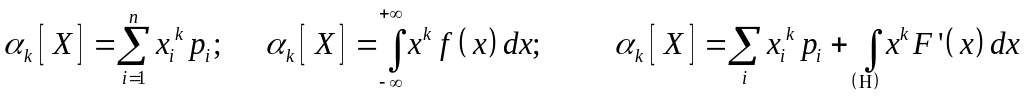
Центральным моментом к-го порядка случайной величины X называется математическое ожидание к-й степени центрированной случайной величины :

Центрированной случайной величиной называется разность между случайной величиной Х и ее математическим ожиданием:

2- Дисперсия

Дисперсией случайной величины X называется математическое ожидание квадрата соответствующей центрированной случайной величины:

Дисперсия вычисляется по формулам:

— для дискретной случайной величины;

— для непрерывной случайной величины;

— для смешанной случайной величины.

3- Средним квадратическим отклонением случайной величины X называется корень квадратный из дисперсии

Математическое ожидание случайной величины X есть ее первый начальный момент, а дисперсия — второй центральный:

Второй и третий центральные моменты выражаются через начальные формулами

2.Понятие о стационарных случайных функциях в широком смысле.

Стационарной случайной функцией X(t) называется случайная функция, математическое ожидание и дисперция которой постоянны,

,

а корреляционная функция зависит только от разности между своими аргументами

3. Задача 10.5.

х – число бросков до первого попадания

р(х=1)=0,4

р(х=2)=(1-0,4)*0,6

р(х=3)=(1-0,4)*(1-0,6)*0,4

р(х=4)=(1-0,4)(1-0,6)(1-0,4)*0,6

р(х=2к+1)=[(1-0,4)(1-0,6)]^к*0,4=0,6^к*0,4^к+1

р(х=2к+2)=[(1-0,4)(1-0,6)]^к*(1-0,4)*0,6=0,6^к+2*0,4^к

где к=0,1,2,…

Экзаменационный Билет №14

1.Биномиальный ЗРВ случайных величин, его числовые характеристики.

Случайная величина , распределенная по биномиальному закону, принимает значения: 0, 1, 2, …, n с вероятностями, определяемыми по формулам Бернулли:

X­i	0	1	2	…		…	n
Pi

 

Математическое ожидание:

Д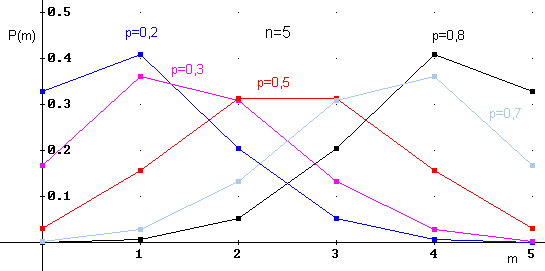 исперсия:

На рисунке приведены многоугольники (полигоны) распределения случайной величины X, имеющей биномиальный закон распределения с параметрами n=5 и p (для  p=0,2; 0,3; 0,5; 0,7; 0,8).