2.Закон больших чисел в форме теоремы Чебышева.

Пусть папарны независимых случайных величин, имеющих математическое ожидание М[X­_i] и дисперцию, ограниченную некоторую постоянную величину с, .

При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.

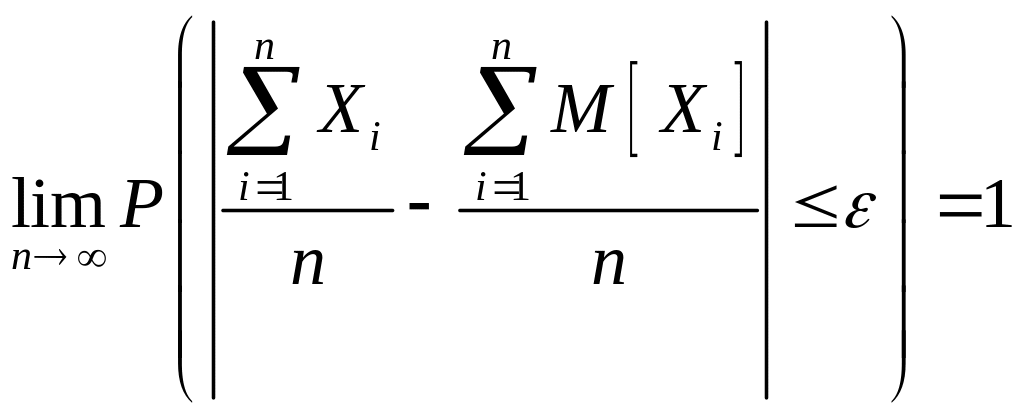
Доказательство

3. Задача 10.3.

X_i – случайное число испытания приборов.

X₁ = 1; X₂ = 2; X₃ = 3; X₄ = 4; X₅ = 5

Потому, что каждый следующий прибор испытается только в том случае, если предыдущий оказал надёжным, вероятность Р_i = P(X = x_i) вычисляется по формуле:

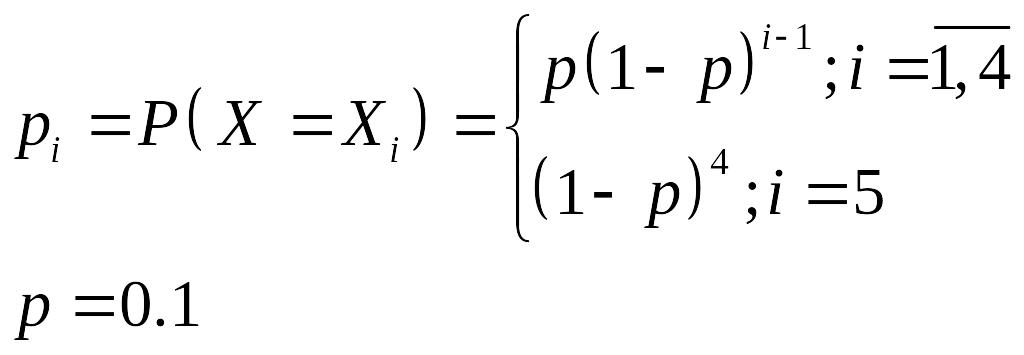
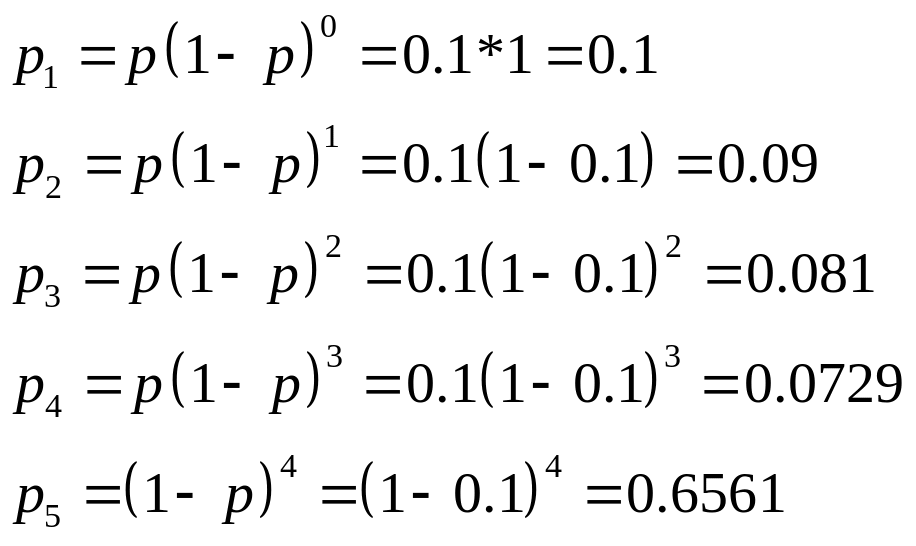
Xi	1	2	3	4	5
pi	0.1	0.09	0.081	0.0729	0.6561

Экзаменационный Билет №11

1 . Плотность распределения случайных величин.

Плотностью распределения непрерывной (в узком смысле слова) случайной величины называется функция f(x) = F'(x).

Плотность распределения любой случайной величины неотрицательна, f(x) > 0, и обладает свойством

График плотности f(x) называется кривой распределения.

Элементом вероятности для случайной величины X называется величина f(x)dx, приближенно выражающая вероятность попадания случайной точки X в элементарный отрезок dx, примыкающий к точке х.

Функция распределения F (х) выражается через плотность распределения формулой

Вероятность попадания случайной величины X на участок от до (включая ) выражается формулой

Е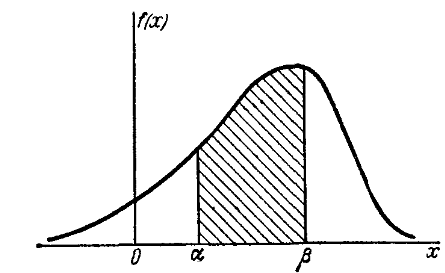 сли случайная величина X непрерывна, то и

Вероятность попадания на участок от до для непрерывной случайной величины выражается формулой

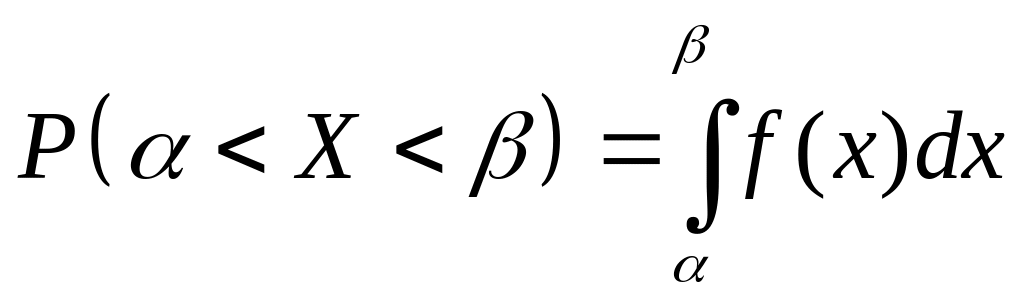
2. Неравенство Чебышева.

Первая формула.

Если х – случайная неотрицательная велична, то

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

2. Для непрерывных величин

b. Вторая формула.

Пусть имеется случайная величина X с математическим ожиданием m_x и дисперсией D_x. Неравенство Чебышева утверждает, что каково бы ни было положительное число а, вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на , ограничена сверху величиной : .

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

2. Для непрерывных величин

Примечание.

Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина X выйдет за пределы участка значительно меньше ¹/₉

3.Задача 12.3.

Мы имеем ряд распределения:

Xi	0	1	2	3	4	5
Pi	0.0672	0.2584	0.3644	0.2344	0.0784	0.0072