2.Следствия закона больших чисел: теорема Бернулли и Пуассона.

Теорема Бернулли.

Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.

Если m число появления события А в n независимых испытаниях с вероятностью успеха в одном испытании p, , то для любого  справедливо .

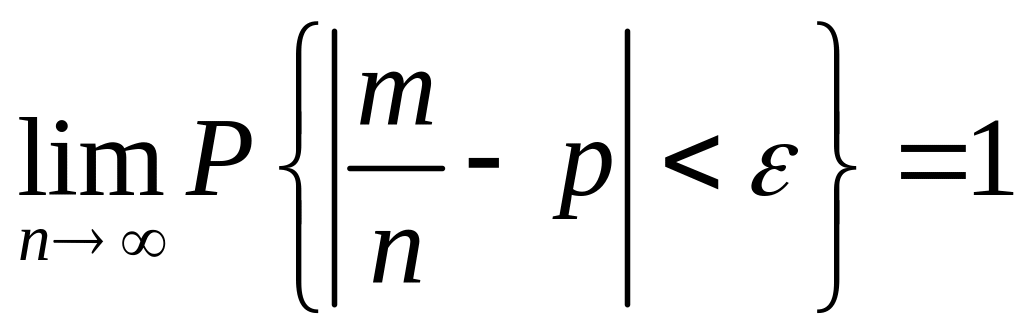
Это означает, что с ростом числа испытаний n относительная частота успехов приближается к вероятности p успеха в одном испытании.

Теорема Пуассона:

Если производится п независимых опытов и вероятность появления события А в i-м опыте равна р_i, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей p_i.

(Если m – число появления в n независимых испытаниях, но каждое испытание имеет свою вероятность, , то для любого  справедливо ).

3. Задача 29.9 (а).

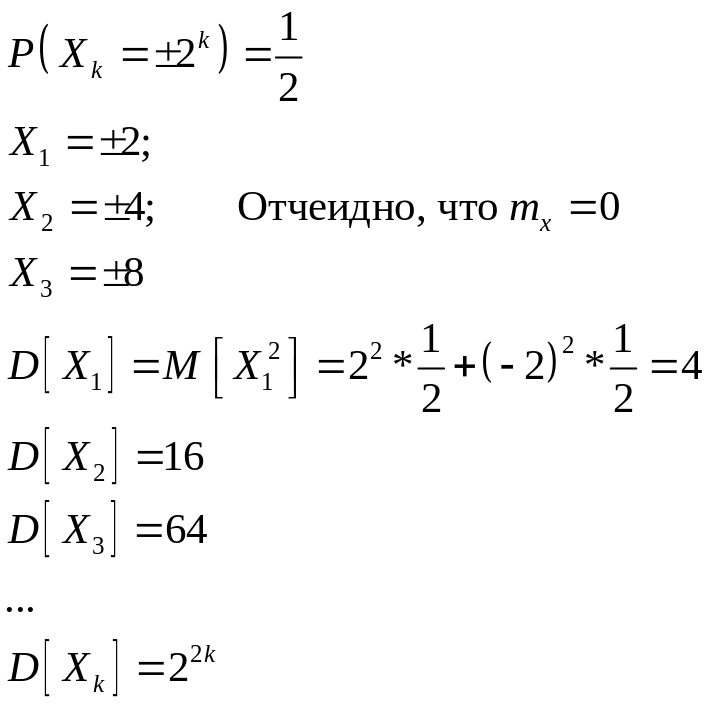
неограничена не выполняет закон больших чисел (по теореме Чейбышева)

Экзаменационный Билет №6

1.Формула полной вероятности

Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий: образующих полную группу несовместных событий. Будем эти события называть гипотезами.

Докажем, что в этом случае

т. е. вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.

Доказательство.

Так как гипотезы образуют полную группу, то событие A может появиться только в комбинации с какой-либо из этих гипотез:

Так как гипотезы несовместны, той комбинации также несовместны; применяя к ним теорему сложения, получим:

Применяя к событию H_iA теорему умножения, получим:

что и требовалось доказать.

2.Понятие об усиленном законе больших чисел.

_{Yn – Сходится по вероятности своему математическому ожиданию.}

Усиленный закон больших чисел утверждает, что при определённом условии наблюдает сходимость почти наверны.

Для того, чтобы последовательность случайных величин подчиняет усиленному закону больших чисел необходимо

Теорема 1: Для того, чтобы последовательность независимых случайных величин подчиняет усиленному закону больших чисел необходимо:

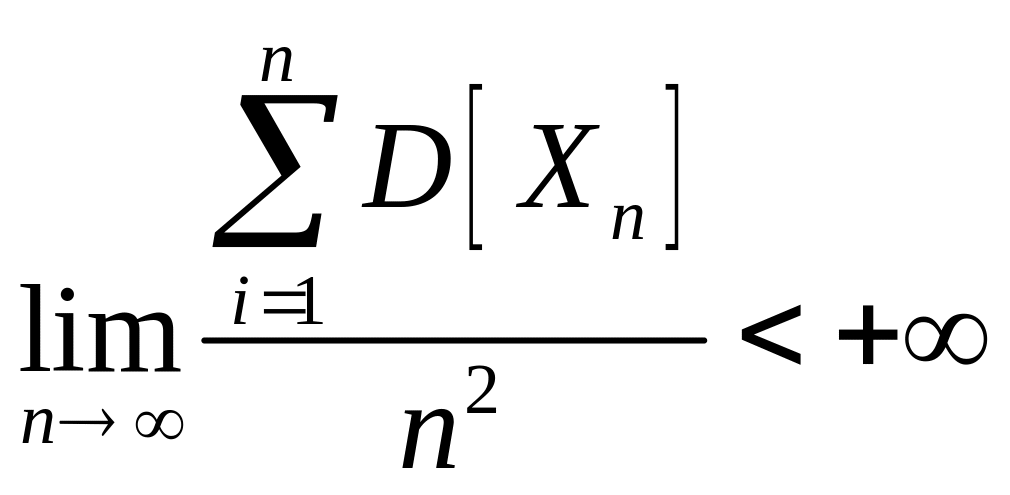
Теорема 2: Последовательность одинаковы распределенных независимых случайных величин подчиняет усиленному закону больших чисел необходимо и достоточно: существование математического ожидания.

3. Задача 15.3.

Срединная ощибка Е = 25

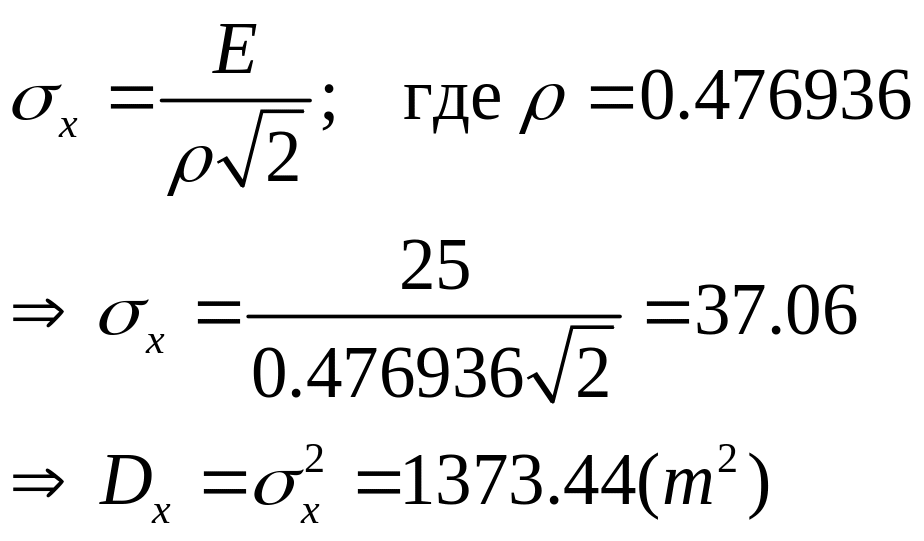
б. Вероятность получения ощибки измерения дальности по абсолютной велчине не превосходящей 20м

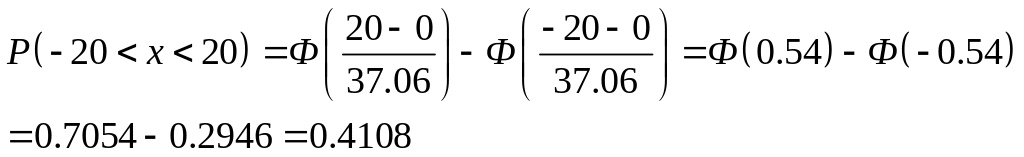
Экзаменационный Билет №7

1.Формула Байеса.

Имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственно Произведен опыт, в результате которого наблюдено появление некоторого события А.

Найти условную вероятность для каждой гипотезы.

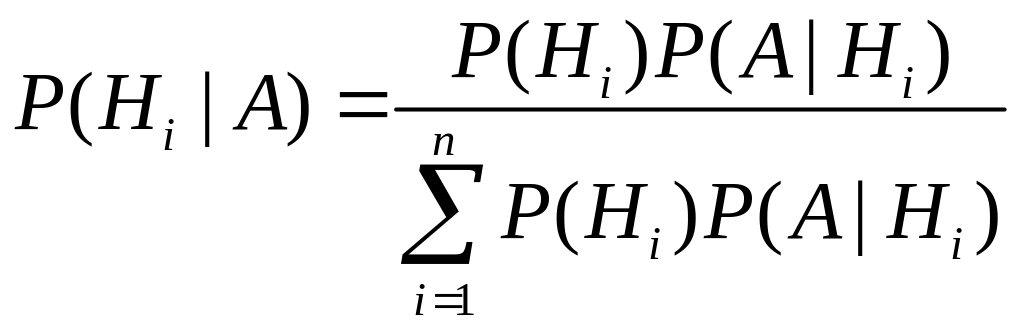
2.Закон больших чисел для зависимых случайных величин.

Теорема Маркова.

Если имеются зависимые случайные величины и если при

то среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

Доказательство. Рассмотрим величину

Применим к величине Y неравенство Чебышева:

Так как по условию теоремы при , то при достаточно большом n

или, переходя к противоположному событию,

что и требовалось доказать.

3. Задача 15.4.

По формуле Бернули

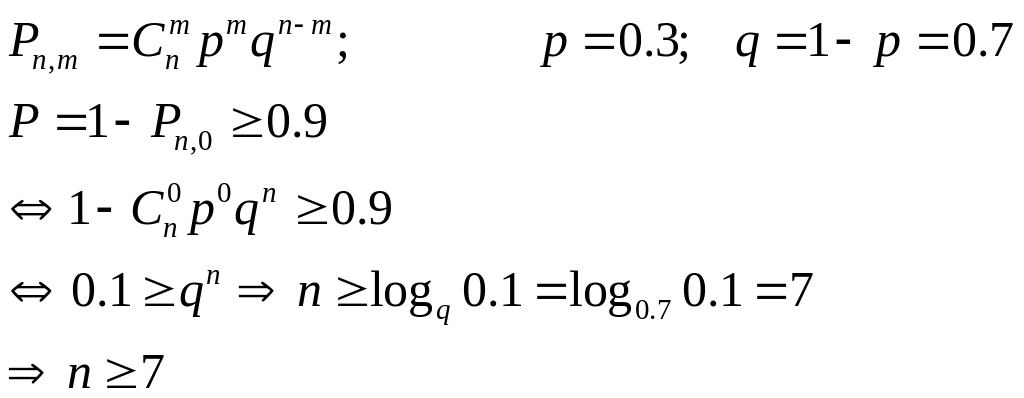
Экзаменационный Билет №8

1.Схема независимых испытаний. Биномиальное распределение.

Нескольно опытов называются независимыми, если вероятность того или иного исхода каждого из овытов не зависит от того, какие исходы имели другие опыты.

Вероятность Р_m,n появления события м раз при n независимых опытах, в каждом из которых вероятность появления события равна р, определяется биномиального распределения:

Где q = 1 – p : вероятность не появления события.

2. Теорема Пуассона, как одна из форм закона больших чисел.

Теорема, устанавливающая свойство устойчивости частот при переменных условиях опыта,

называется теоремой Пуассона и формулируется следующим образом:

Если производится п независимых опытов и вероятность появления события А в i-м опыте равна р_i, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей p_i.

3.Задача 13.9.

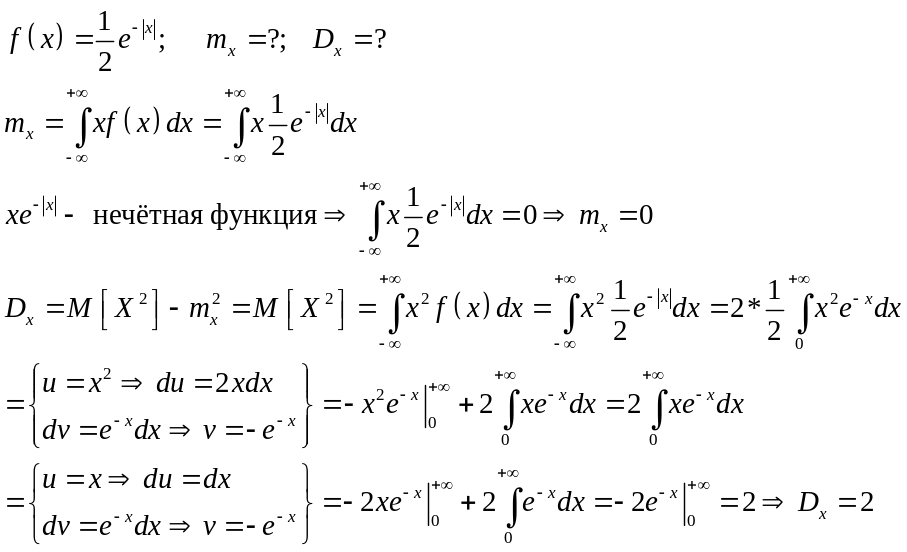
Экзаменационный Билет №9

1.Обобщение схемы независимых испытаний. Локальная теорема Муавра – Лапласа.

1. Пусть производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, причем вероятность появления события А в i-м опыте равна p_i, а вероятность непоявления qi=1 – pi (i= 1...n). Требуется найти вероятность Р_m,n того, что в результате n опытов событие А появится ровно m раз.

Вероятность того, что событие А в n независимых опытах появится ровно m раз, равна коэффициенту при x^m в выражении производящей функции:

где p_i — вероятность появления события А в i-м опыте, q_i = 1 – p_i

2. Пусть производится n независимых опытов, в каждом из которых событие

А₁ появится m₁ раз с вероятностью p₁

А₂ появится m₂ раз с вероятностью p₂

_{......................}

А_k появится m_k раз с вероятностью p_k

И . Требуется найти вероятность Рn,m₁m₂,...,m_k того, что в результате n опытов событие А_i появится ровно m_i раз.

Такая вероятность равна коэффициенту при в выражении производящей функции:

Локальная теорема Муавра – Лапласа.

Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина ограничена равномерно по m и n , то

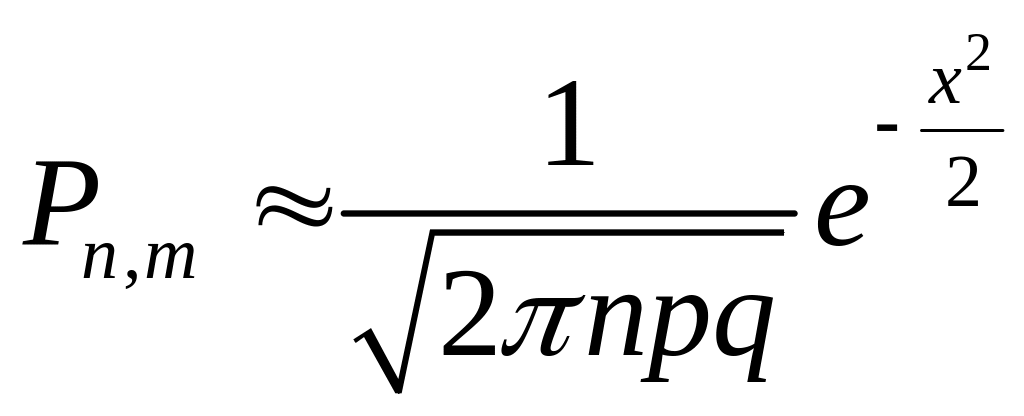
Эта формула работает плохо при малых р, а хорошо при р = q

2.Теорема Бернулли, как одна из форм закона больших чисел.

Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.

Если m число появления события А в n независимых испытаниях с вероятностью успеха в одном испытании p, , то для любого  справедливо .

Это означает, что с ростом числа испытаний n относительная частота успехов приближается к вероятности p успеха в одном испытании.

3. Задача 13.1 (а,б).

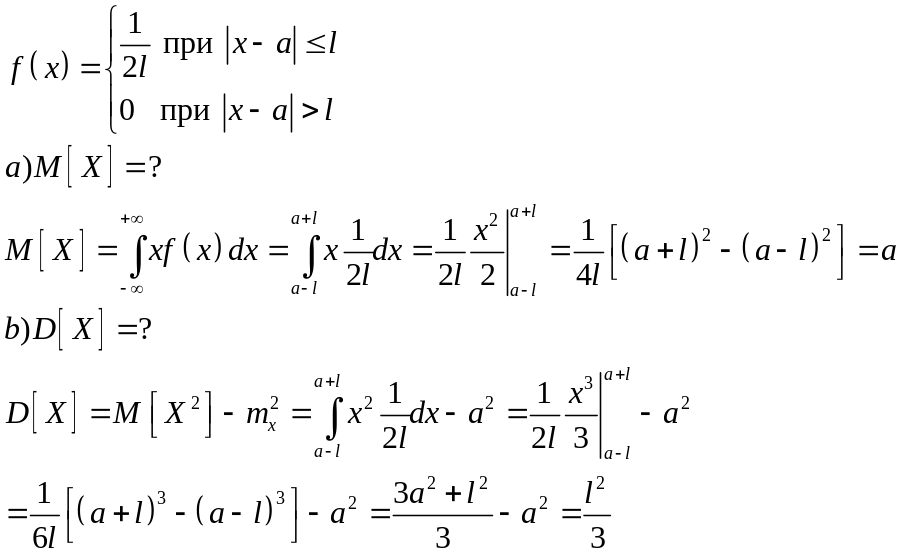
Экзаменационный Билет №10

1.Функции распределения случайных величин.

Функцией распределения случайной величины X называется функция F(х), выражающая вероятность того, что X примет значение, меньшее чем х:

F(x) = P(X <x).

Функция F (х) есть неубывающая функция;

Для дискретных случайных величин функция распределения есть разрывная ступенчатая функция, непрерывная слева.

Если функция распределения F (х) везде непрерывна и имеет производную, случайная величина называется непрерывной в узком смысле слова или просто непрерывной.

Если функция распределения F (х) на некоторых участках непрерывна, а в отдельных точках имеет разрывы, случайная величина называется смешанной.