2.Полиномиальное распределение вероятностей (второе обобщение схемы независимых испытаний).

Пусть производится n независимых опытов, в каждом из которых событие

А₁ появится m₁ раз с вероятностью p₁

А₂ появится m₂ раз с вероятностью p₂

_{......................}

А_k появится m_k раз с вероятностью p_k

И . Требуется найти вероятность Р_n,_m1m2,...,mk того, что в результате n опытов событие А_i появится ровно m_i раз.

Такая вероятность равна коэффициенту при в выражении производящей функции:

3. Задача 30.3 (в )

Вероятность выхода из строя от 14 до 26 конденсаторов:

Экзаменационный Билет №4

1.Теорема умножения вероятностей.

Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.

Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Условной вероятностью события А при наличии В называется вероятность события А, вычисленная при условии, что событие В произошло. Эта вероятность обозначается Р (А/В).

События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий .

Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого:

Р(АВ) = Р(А) Р(В\А) или Р(АВ) = Р(В) Р(А\В).

Для независимых событий А и В: Р(АВ) = Р(А)Р(В).

Теорема умножения вероятностей для нескольких событий

Р(А₁А₂...А_n) = Р(А₁)Р(А₂\А₁)Р(А₃\А₁А₂)...Р(А_n\А₁А ...А_n-1).

В случае, когда события независимы, т.е. появление любого числа из них не меняет вероятностей появления остальных.

2.Два примера применения центральной предельной теоремы.

а) Пусть — независимые случайные величины с математическими ожиданиями и дисперсиями

Предположим, что условия центральной предельной теоремы выполнены и число слагаемых п достаточно для того, чтобы закон распределения величины можно было считать приближенно нормальным.

Тогда вероятность того, что случайная случайная величина У попадает в пределы участка , выражается фопмулой

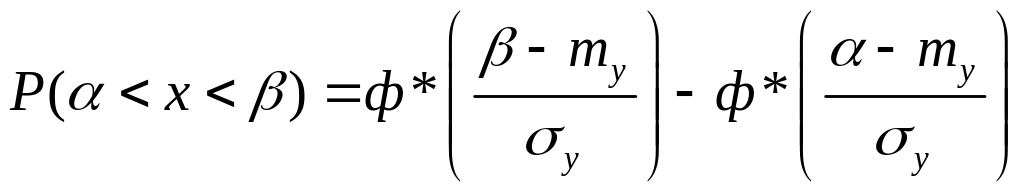
Где математическое ожидание и среднее квадратическое отклонение величины V,

Ф* — нормальная функция распределения.

b) Частным случаем центральной предельной теоремы для дискретьых случайных величин является теорема Лапласа.

Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение

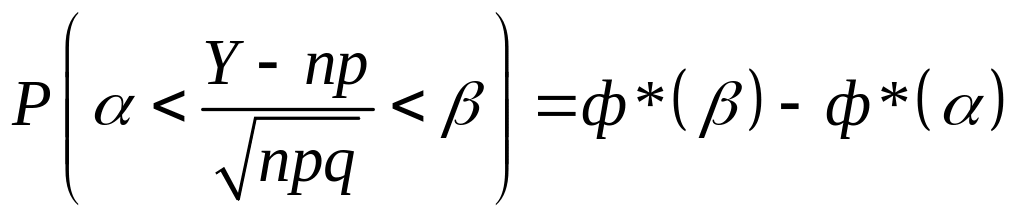
где Y — число появлений события А в n опытах, q = l — р.

3. Задача 29.6

xi		0
p1

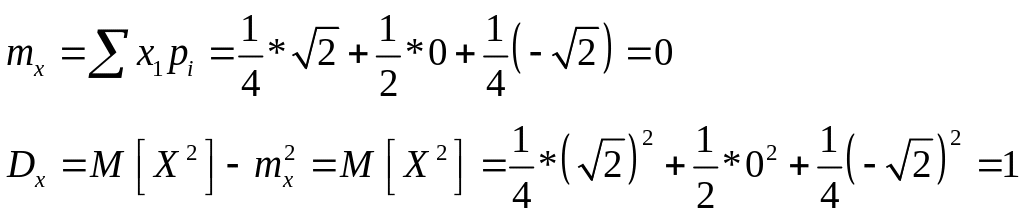
Дисперсия , поэтому по теореме Чейбыева для попарно независимых случайных величин зедсь выполняется закон больших чисел.

Экзаменационный Билет №5

1.Независимые и зависимые события.

Событие А называется независимым от события В, если вероятность события А не зависит от того, роизошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Рассмотрим примеры.

1) Опыт состоит в бросании двух монет; рассматриваются события:

А — появление герба на первой монете,

В — появление герба на второй монете.

В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А независимо от события В.

2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события:

А — появление белого шара у 1-го лица,

В — появление белого шара у 2-го лица.

Вероятность события А до того, как известно что-либо о событии В, равна ²/₃ Если стало известно, что событие В произошло, то вероятность события А становится равной ¹/₂, из чего заключаем, что событие А зависит от события В.