Экзаменационный билет №2

1. Классическая, частотная, геометрическая схема вычисления вероятности.

а- Классическая вероятность

Вероятность события А вычисляется по формуле ;

где n - общее число случаев;

m - число случаев, благоприятных событию А.

b- Частота

Частоту события часто называют его статистической вероятностью. Частота события вычисляется на основании результатов опыта по формуле и отчевидно, что

где m— число появлений события А;

n — общее число произведенных опытов.

с- Геометрическая вероятность:

Использована тогда, когда вероятность попадания случайной точки в любую часть области пропорциональна мере этой части области (длине, площади, объёму, ...) и не зависит от её расположения и формы.

2.Неравенство Чебышева. Две формы неравенства Чебышева.

a. Первая формула.

Если х – случайная неотрицательная велична, то

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

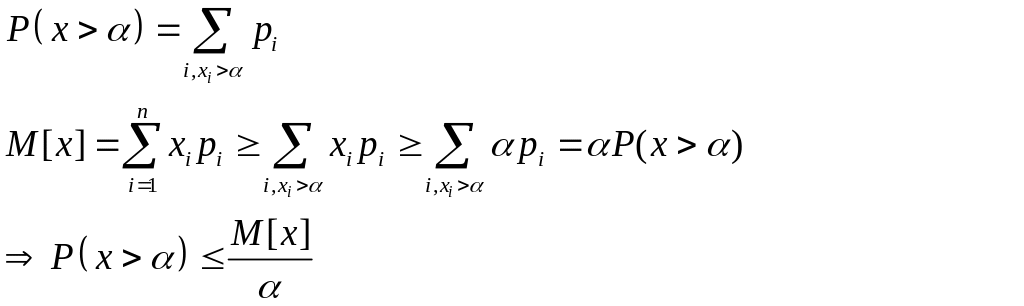
2. Для непрерывных величин

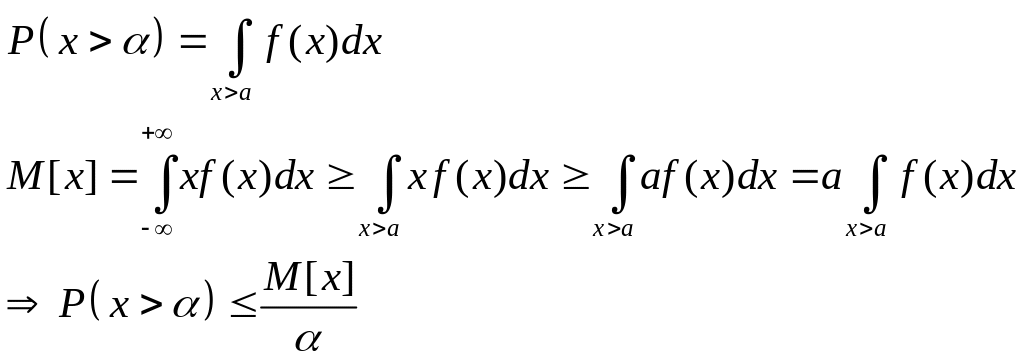
b. Вторая формула.

Пусть имеется случайная величина X с математическим ожиданием m_x и дисперсией D_x. Неравенство Чебышева утверждает, что каково бы ни было положительное число , вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на , ограничена сверху величиной : .

Доказательство:

1.Пусть величина X прерывная, с рядом распределения

xi	x1	x2	...	xn
p1	p1	p2	...	pn

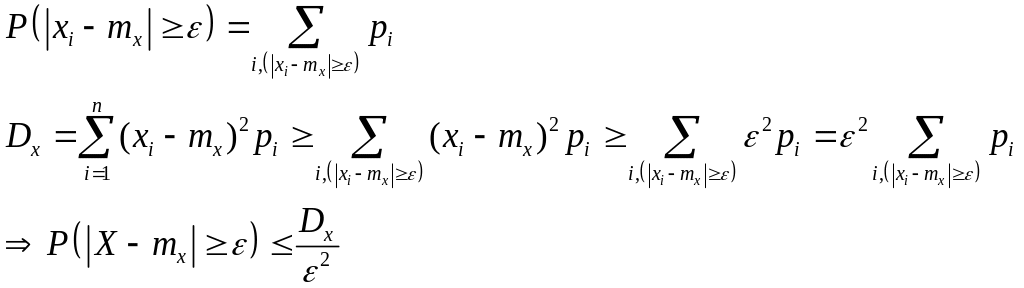
2. Для непрерывных величин

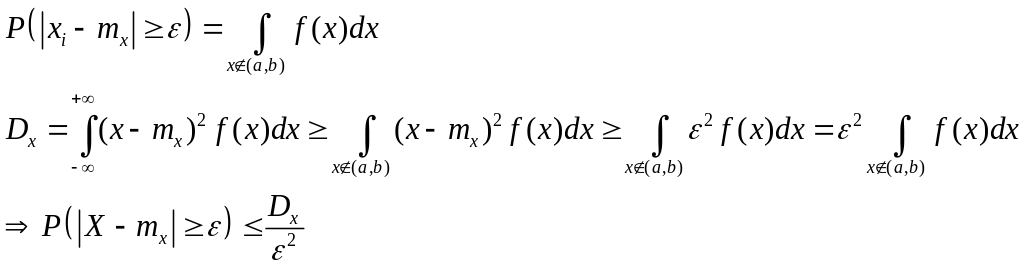
Примечание.

Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина X выйдет за пределы участка значительно меньше ¹/₉

3. Задача 30.3. (б)

Вероятность выхода из строя менее 28 конденсаторов:

Экзаменационный Билет №3

1.Теорема сложения вероятностей.

Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Теорема сложения вероятностей

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(В).

Доказательство:

Предположим, что из n случаев m благоприятны событию А,a k — событию В. Тогда

Так как события А и В несовместны, то нет таких случаев,которые благоприятны я А, и В вместе. Следовательно, событию A+B благоприятны m+k случаев и

В случае, когда события А и В совместны, вероятность их суммы выражается формулой

Р(A + В) = Р(A) + Р(В) - Р(АВ),

где АВ — произведение событий А и В.

Теорема сложения вероятностей для нескольких событий

Вероятность суммы нескольких несовместных событий равна сумме их вероятностей:

В случае, когда события A_i совместны, вероятность их суммы выражается формулой

где суммы распространяются на все возможные комбинации различных индексов г, j, к,..., взятых по одному, по два, по три и т. д.

Если события A₁,А₂,..., А_n несовместны и образуют полную группу, то сумма их вероятностей равна единице:

Событие называется противоположным событию А, если оно состоит в непоявлении события А.

Сумма вероятностей противоположных событий равна единице: